Интеллектуальный вендинг
Автор идеи и разработчик: GlebsHP.
Заметим, что в любом случае Аркадий не может потратить больше денег, чем у него есть, поэтому количество купленных бутылок не превзойдёт 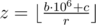 . Однако, может так получится, что Аркадию придётся купить меньше бутылок, если в какой-то момент у Аркадия не будет хватать мелочи на покупку без сдачи, а нужно количество сдачи в автомате не будет.
. Однако, может так получится, что Аркадию придётся купить меньше бутылок, если в какой-то момент у Аркадия не будет хватать мелочи на покупку без сдачи, а нужно количество сдачи в автомате не будет.
Заметим, что суммарное количество мелочи в обороте не меняется и составляет c + d. При этом, если c + d ≥ 999 999, то либо у Аркадия всегда найдётся мелочь, чтобы купить очередную бутылку, либо автомат сможет дать сдачу, если платить только с помощью банкнот. В этом случае ответ равен z.
Если же c + d < 999 999, то может быть, что у Аркадия хватает мелочи для совершения покупки без сдачи, может быть, что в автомате достаточно сдачи для покупки банкнотами, но не может быть одновременно выполнено и то и другое, а значит, действия Аркадия определяются однозначно. В этом случае можно было бы промоделировать его действия, однако, их может оказаться слишком много.
Обозначим через ai количество монет у Аркадия после первых i действий (то есть a0 = c). Заметим, что если ai = aj, то ai + 1 = aj + 1 (действительно, следующее действие однозначно определяется величиной ai), а значит последовательность зацикливается и повторяется. Будем моделировать действия Аркадия по покупке бутылок напитка Квас-Класс, до тех пор пока какое-то из значений ai не повторится, либо не возникнет ситуация, когда Аркадий не может совершить следующую покупку. В случае повторения значения ai в качестве ответа выведем величину z, в противном случае номер итерации, на котором не получилось совершить очередную покупку.
Упражнение: придумайте решение задачи, если все банкноты имеют номинал 1012.
НВП против НУП
Автор идеи и разработчик: Endagorion.
Нарисуем на плоскости n точек pi = (i, ai). Пусть I = (i1, ..., ik) и J = (j1, ..., jl)~--- пара непересекающихся НВП и НУП. Из максимальности I следует, что строго внутри следующих прямоугольников не содержится точек (прямоугольники описываем координатами противоположных углов):
A0 = ((0, 0), pi1);
Ax = (pix, pix + 1) для всех 1 ≤ x < k;
Ak = (pik, (n + 1, n + 1)).
Аналогично, поскольку J максимальна, не может быть точек в следующих прямоугольниках:
B0 = ((0, n + 1), pj1);
By = (pjy, pjy + 1) для всех 1 ≤ y < l;
Bl = (pjl, (n + 1, 0)).
Эти две цепочки прямоугольников соединяют пары противоположных углов квадрата ((0, 0), (n + 1, n + 1)). В предположении, что I и J не пересекаются, у нас обязательно дожна быть пара пересекающихся прямоугольников Ax и By. Поскольку никакие прямоугольники Ax и By не содержат точек, есть всего два случая, как они могут пересечься:
ix < jy < jy + 1 < ix + 1, ajy + 1 < aix < aix + 1 < ajy (как в первом примере);
jy < ix < ix + 1 < jy + 1, aix < ajy + 1 < ajy < aix + 1 (зеркальное отражение предыдущего).
Поищем пересечения типа 1 (для типа 2 перевернем перестановку и поищем еще раз). Скажем, что (i, i') является {\it НВП-парой}, если a и b являются последовательными элементами в какой-то НВП (аналогично определим {\it НУП-пару}). Пускай существуют НВП-пара (i, i') и НУП-пара (j, j'), удовлетворяющие i < j < j' < i' и aj' < ai < ai' < aj, то есть какие-то НВП и НУП имеют пересечение типа 1. Это означает, что ответ можно найти, построив все НВП- и НУП-пары и поискав такое пересечение.
Конечно, всевозможных пар слишком много. Однако, заметим, что в ситуации выше мы можем заменить i' на  , а j' на
, а j' на  . Поэтому можно оставить в рассмотрении O(n) пар. Пересечения среди них поищем сканирующей прямой с деревом отрезков.
. Поэтому можно оставить в рассмотрении O(n) пар. Пересечения среди них поищем сканирующей прямой с деревом отрезков.
Прогулки за едой
Автор идеи и разработчик: GlebsHP.
Сначала решим версию задачи, в которой изначальное перемещение совершается бесплатно, а после x съеденных единиц еды перемещение на 1 стоит x. Несложно видеть, что оптимальной стратегией будет дойти до какой-то позиции k, а затем двигаться только в сторону позиции 0, заходя в какие-то рестораны. Пусть мы зашли в ресторан i, тогда вес увеличился на ai и каждое перемещение также стало на ai дороже. Поскольку в оптимальной стратегии мы посещаем рестораны только двигаясь в сторону позиции 0, то можно сразу сказать, что посещение ресторана i в итоге обойдётся в ai·i единиц энергии.
Получаем задачу о рюкзаке, есть n предметов, i-й из них имеет вес ai·i и стоимость ai, требуется выбрать подмножество предметов с максимальной суммарной стоимостью и весом не более e. Стандартный способ решения такой задачи предполагает использовать динамическое программирование d(i, x) — максимально возможная суммарная стоимость, если из первых i предметов набрать подмножество веса x.
Произведём замену параметра, будем вычислять динамическое программирование d(i, c) — минимально возможный вес, если из первых i предметов выбрать подмножество суммарного веса c. Далее, будем добавлять предметы в порядке уменьшения значения i, то есть для получения d(i, c) можно использовать только рестораны с i-го по n-й. Какие значения параметра c имеет смысл рассматривать? Любая единица стоимости (то есть насыщения в терминах исходной задачи), полученная в ресторанах с номерами ≥ i требует затрат хотя бы i единиц энергии, поэтому имеет смысл рассматривать только 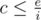 . Воспользуемся формулами оценки суммы гармонического ряда и получим, что количество значений динамического программирования, которые нам требуется вычислить оценивается как
. Воспользуемся формулами оценки суммы гармонического ряда и получим, что количество значений динамического программирования, которые нам требуется вычислить оценивается как 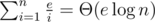 .
.
Последним штрихом будет учесть исходную стоимость перемещения до позиции, где будет посещён ресторан с наибольшим индексом. Пусть эта будет ресторан k, тогда к ответу требуется прибавить 2k, что можно учесть в момент перехода из состояния d(i, 0) при вычислении значений динамического программирования.
Поисковик
Автор идеи: GlebsHP, разработка задачи: cdkrot.
Для начала заметим, что в конце, после приписывания всех букв, Алиса получит в точности строку s.
Действительно, пусть мы приписывали буквы, и оставались внутри строки, а потом после некоторого приписывания все вхождения пропали. Тогда все дальнейшие приписывания не увеличивают итоговую сумму, а вместо этого можно было бы выделить на том роковом шаге одно из вхождений, и просто растить слово влево и вправо до границ s.
Воспользуемся этим знанием, чтобы решить задачу. В частности, можно развернуть процесс: скажем, что нам изначальна дана строка s, а затем из неё постепенно выкидывают буквы слева или справа.
Построим по строке суффиксное дерево, то есть бор, в который добавили все суффиксы строки s.
Будем делать динамику от вершины — dp[v] = максимальной сумме, которую можно получить, если начать со строки, соответствующей пути от корня до v и выкидывать буквы с краёв, считая сумму вхождений по всей большой строке s.
В этой динамике всего два перехода — можно подняться в предка (что соответствует выкидыванию буквы справа), или перейти по суффиксной ссылке (что соответствует выкидыванию буквы слева). Считать динамику можно лениво, а количество вхождений~--- это количество терминальных вершин в поддереве (что можно предподсчитать заранее для всех вершин).
Правда, чтобы в динамике было меньше n2 состояний, придётся перейти к сжатому суфдереву.
В таком случае, переход в предка может соответствовать выкидыванию сразу нескольких букв справа, в таком случае посередине этого ребра количество вхождений совпадает с количеством вхождений у нижнего конца ребра. Аналогично дела обстоят и с суффиксной ссылкой.
Единственное что мы не учли, так это то, что возможно в оптимальном ответе переходы наверх по ребру и по суффиксной ссылке "перемешаны", и из-за сжатия суфдерева мы таких переходов не увидим. На самом деле это ничего не портит. Действительно, если мы поднимались по длинном ребру, сделали переход по суфссылке и доподнимались по ребру, то можно было сразу пойти по суфссылке, а уж затем подниматься по ребру — количество вхождений от такой перестановки может только увеличится.
Асимптотика решения — 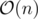 , задачу можно также решить с помощью суффиксного автомата и динамики на нём, в таком случае переходами динамики тоже являются суффиксные ссылки и обратные рёбра.
, задачу можно также решить с помощью суффиксного автомата и динамики на нём, в таком случае переходами динамики тоже являются суффиксные ссылки и обратные рёбра.
Упражнение: решите задачу, если в качестве стартовой строки даётся не пустая строка, а некоторая подстрока исходной строки, заданная как границы вхождения (li и ri). При этом требуется решить задачу для 100 000 различных запросов.
Угадай меня, если сможешь
Автор идеи и разработчик: GlebsHP.
Заметим, что если мы по очереди назовём все элементы в каком-нибудь порядке, то в завершении ситуация будет аналогична исходной, но со сдвигом на 1. Такой сдвиг никак не влияет ни на ответ, ни на промежуточные значения, возвращаемые интерактором.
Посмотрим на тройку элементов i, j и k, такую что pi + 1 = pj = pk - 1. В случае, если мы перечислим все элементы в таком порядке, что j будет идти раньше i и раньше k, то в момент когда pj увеличится на один, количество различных элементов уменьшится и мы сможем с уверенностью сказать, то на позиции j не находится максимум.
Выберем случайную перестановку и назовём элементы в соответствующем ей порядке. В тройке i, j, k, описанной выше, вероятность того, что j будет назван раньше i и k составляет  . Таким образом, если проделать эту операцию 50 раз, используя каждый раз новую случайную перестановку, то вероятность, что элемент j не являющийся максимумом всё ещё не будет помечен составляет лишь
. Таким образом, если проделать эту операцию 50 раз, используя каждый раз новую случайную перестановку, то вероятность, что элемент j не являющийся максимумом всё ещё не будет помечен составляет лишь 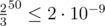 . Поскольку события выполнения для каждой тройки i, j, k нельзя назвать независимыми, то оценим вероятность ошибки хотя бы на одном элементе как 2·10 - 9·n ≤ 2·10 - 6 в указанных ограничениях.
. Поскольку события выполнения для каждой тройки i, j, k нельзя назвать независимыми, то оценим вероятность ошибки хотя бы на одном элементе как 2·10 - 9·n ≤ 2·10 - 6 в указанных ограничениях.
Хеширование для ленивых
Автор идеи GlebsHP. Разработка задачи: Arterm.
Заметим, что 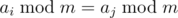 если и только если m|ai - aj. Следовательно, надо найти наименьшее m, не делящее ни одну разность чисел в данном массиве.
если и только если m|ai - aj. Следовательно, надо найти наименьшее m, не делящее ни одну разность чисел в данном массиве.
Для начала найдем все разности. Положим
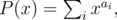
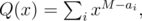
где M = max ai. Вычислим произведение T(x) = P(x)·Q(x) с помощью быстрого преобразования Фурье. Так как
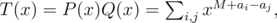
то коэффициент при xM + d ненулевой тогда и только тогда в массив a если два числа с разностью d.
Теперь для каждого m на отрезке [1, M] проверим, если ли среди разностей кратная m. Сделать это мы можем за 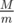 . Так мы найдем ответ на задачу за время
. Так мы найдем ответ на задачу за время 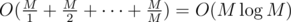 .
.
Сложность работы обоих частей 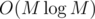 , где M = max ai ≤ 2 000 000.
, где M = max ai ≤ 2 000 000.






