Понимание того, как построить гамильтонов цикл в строго связном турнире, основываясь на его свойствах, простым конструктивом, было критично на региональном этапе всероссийской олимпиады школьников по информатике в сезоне 2014/2015 для получения полного балла по задаче Магические порталы (здесь можно дорешать).

Пусть дан ориентированный граф, в котором между любыми двумя вершинами есть направленная дуга, а также для любой пары вершин u и v можно дойти из u в v по ориентированным дугам, а затем успешно вернуться также по ориентированным дугам обратно (**строго связный турнир**). Пример такого графа:

В таком графе есть гамильтонов путь — путь, проходящий по всем вершинам (например: ), и гамильтонов цикл — гамильтонов путь, в котором из конца есть дуга в начало (например: ). Рассмотрим алгоритм нахождения и того, и того за O(n²).

Гамильтонов путь в строго связном турнире

Удобнее всего строить по индукции. Пусть уже есть путь 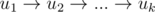из k вершин. Надо добавить к нему новую вершину u_k + 1. Делаем следующее:

1. Находим максимальный номер i такой, что из любой вершины u₁, u₂, ..., u_i ведет ребро в u_k + 1.

2. Вставляем новую вершину после u_i, получая путь:

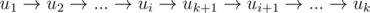
Здесь активно используется тот факт, что граф у нас — строго связный турнир, а это значит, что если из u в v нет дуги, то точно есть дуга из v в u.

Начиная с пустого пути, добавляем в него все вершины по очереди, каждая операция вставки требует O(n) действий, всего нужно вставить n вершин, следовательно, спустя O(n²) действий получим гамильтонов путь.

Можно сделать это за O(nlog(n)) — подробнее в прикрепленных источниках.

Гамильтонов цикл в строго связном турнире

Стратегия следующая: раз мы уже умеем находить гамильтонов путь, то сперва найдем его за O(n²), а затем уже преобразуем в гамильтонов цикл за O(n²) действий (можно сделать это за O(n) — подробнее в прикрепленных источниках).

После нахождения гамильтонова пути 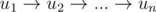необходимо перестроить его в цикл, обеспечив наличие ребра из последней вершины цикла в первую. Сделаем небольшие приготовления:

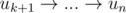Пойдем по всем вершинам пути u₃, u₄, ..., u_k до тех пор, пока есть ребро из u_k в u₁. Если дошли до конца пути, то цикл найден — это весь путь, иначе есть некий цикл и остаток пути . Далее будем по индукции расширять цикл, добавляя вершины из пути. Рассмотрим два случая:

1. Если в цикле есть вершина, в которую идет ребро из добавляемой вершины u_k + 1, то находим первую такую вершину u_i. Теперь мы можем составить новый цикл 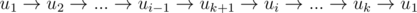, а путь будет выглядеть как .

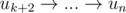2. Если в цикле не нашлось вершины, в которую бы шло ребро из добавляемой вершины u_k + 1, пройдем по остальным вершинам пути, пока не найдем вершину u_j, для которой такая вершина u_i все же найдется (такая вершина должна быть, иначе этот граф не строго связный турнир, так как мы нашли способ его разбиения на две компоненты строгой связности). Тогда все вершины из начала пути до u_j добавляем в цикл, перестраивая его следующим образом: 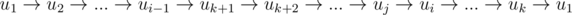. От пути либо ничего не остается, либо остается .

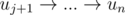На каждой итерации мы увеличиваем длину цикла как минимум на 1, выполняя при этом O(n) операций. Итоговая асимптотика алгоритма O(n²).

Что почитать?

В приведенных источниках есть способ нахождения гамильтонова пути и цикла за O(nlog(n)) со структурой данных Semi-Heap, который можно применять на строго связных турнирах, состоящих из порядка 200.000 вершин, а направление ребер в которых определяется некоторой функцией f(u, v) от номеров вершин:

1. On Finding a Hamiltonian Path in Tournament Using Semi-Heap (Part 1: Sequential Solution) — Jie Wu

2. A linear-time algorithm for finding Hamiltonian cycles in tournaments — Y.Manoussakis