This is the second problem of Div.3. But I think it is not easy.

Problem:1029B - Creating the Contest

Simple Meaning of Problem:

There is a sequence a and you should choose the longest sequence b {a_i1, a_i2, ..., a_ip} (p is the length of b) such that:each j∈[1, k) a_ij + 1 ≤ a_ij·2 should hold.

print the maximum number of p (the length of b)

First, you can enumerate which ones to choose. You will get a algorithm with O(2ⁿ). And you will get a Time Limit Exceed.(I didn't write it, because it is valueless.)

Then, dp is another useful algorithm. (But this problem can be solved by greedy. Please view the official tutorial of it.) So we can try to use dp.

f[i] means that if you choose the number a_i, you can get the maximum p (only of 1 to i).

It is very easy to get the state transition equation:

f[i] = max{f[j]} + 1, j satisfy that a_i ≤ a_j·2 and j ≤ i.

And the answer is max{f[i]} (i is 1 to n).

code:42093398

#pragma comment (linker,"/STACK:1024000000") 
#pragma GCC optimize(2)
#pragma GCC target(arch=corie7-acx)
#include<bits/stdc++.h>
using namespace std;
int n,a[200001],f[200001];
deque <int> q;
int t,ans;
int main()
{
	scanf("%d",&n);
	for (int i=1;i<=n;i++)
	scanf("%d",&a[i]);
	f[1]=1;
	for (int i=2;i<=n;i++)
	{
		for (int j=1;j<=i-1;j++)
		if (a[j]*2>=a[i]) f[i]=max(f[i],f[j]);
		f[i]++;
	}
	for (int i=1;i<=n;i++)
	ans=max(ans,f[i]);
	printf("%d",ans);
	return 0;
}

And this code does better:42095786(In fact, it also Time Limit Exceed on Test 4)

#pragma comment (linker,"/STACK:1024000000") 
#pragma GCC optimize(2)
#pragma GCC target(arch=corie7-acx)
#include<bits/stdc++.h>
using namespace std;
int n,a[200001],f[200001];
deque <int> q;
int t,ans;
int main()
{
	scanf("%d",&n);
	for (int i=1;i<=n;i++)
	scanf("%d",&a[i]);
	f[1]=1;
	for (int i=2;i<=n;i++)
	{
		for (int j=i-1;j>=1;j--)
		if (a[j]*2>=a[i]) f[i]=max(f[i],f[j]);
			else break;
		f[i]++;
	}
	for (int i=1;i<=n;i++)
	ans=max(ans,f[i]);
	printf("%d",ans);
	return 0;
}

But, unfortunately, these two are both Time Limit Exceed. (Actually, it is inevitable.)

Because when a_n ≤ a₁·2, the time complexity of the code will come to O(n²) (break is useless).

So it is inevitable that the code will TLE.

Now, how can we optimize our algorithm?

In the problem, notice that the numbers are increasing.

So when i is increasing, a_i is increasing, too. And 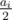is increasing, so the number which is less than 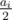is also increasing.

Because of this, for the increasing number i, the j which is satisfy a_i ≤ a_j·2 is increasing as well.

So we can maintain a queue. The number of the queue means the number of a's number.

When we want to calculate f[i], we check the numbers of queue from the front to the back. For each x, if a_x·2 < a_i, we can pop x. (Because for the after j, a_j ≥ a_i > a_x·2).

We can find the first x which is satisfy a_x·2 ≥ a_i. Then we use f[x] to calculate f[i]. (It will be proven after).

Finally, we get the back of q y. If f[y] ≤ f[i], we can pop y. That's because y must be popped earlier than i, and f[i] is greater than f[y]. So the following number choose f[i] is greater than f[y].

And that's why the first number of the queue x is the best choice to transfer f[i] after popping. (In fact, it is a priority queue.)

When we code it, we can use double-end-queue (deque).

code:42036114

#pragma comment (linker,"/STACK:1024000000") 
#pragma GCC optimize(2)
#pragma GCC target(arch=corie7-acx)
#include<bits/stdc++.h>
using namespace std;
int n,a[200001],f[200001];
deque <int> q;
int t,ans;
int main()
{
	scanf("%d",&n);
	for (int i=1;i<=n;i++)
	scanf("%d",&a[i]);
	f[1]=1;
	q.push_back(1);
	for (int i=2;i<=n;i++)
	{
		while (!q.empty())
		{
			t=q.front();
			if (a[t]*2<a[i]) q.pop_front();
				else break;
		}
		if (q.empty()) t=0;
		f[i]=f[t]+1;
		while (!q.empty())
		{
			t=q.back();
			if (f[t]<f[i]) q.pop_back();
				else break;
		}
		q.push_back(i);
	}
	for (int i=1;i<=n;i++)
	ans=max(ans,f[i]);
	printf("%d",ans);
	return 0;
}

Thank you for reading my first entry. See you next time!

postscripts:

1. It is the first time of mine to write an entry. So if there is any mistake, please specify (Theory_of_Everything). Thanks.
2. Oh, writing an entry is so tiring!