This blog is just a back up of http://codeforces.net/blog/entry/57319 to prevent this tutorial from discarding after jiry_2 is banned.
Hi, I’d like to introduce a simple trick about segment tree in this blog as I promised in this comment. Sorry for the long delay, as a sophomore in Peking University, I've just finished a tired semester and a painful final exam. And now I finally have enough time to do a simple introduction to this interesting algorithm.
It may be a huge project for me since my English is not good. I think I will finish this blog in several steps and I will try to finish it as soon as possible :)
In China, all of the 15 candidates for the Chinese National Team are asked to write a simple research report about algorithms in informatics Olympiad, and the score will be counted in the final selection. There are many interesting ideas and algorithms in these reports. And I find that some of them are quite new for competitors in CF although they are well known in China from the final standings of some recent contests. For example, In the last contest CF Round #458, the problem G can be easily solved using "power series beats" (Thanks for matthew99 to give this name :)) in O(2nn2) which was imported in China by vfleaking in 2015.
This blog is about my report which is written about two years ago. I am satisfied with this work although there is a flaw about time complexity. xyz111 gave me a lot of inspiration, and the name “Segment tree beats” is given by C_SUNSHINE which is from a famous Japanese anime “Angel Beats”.
Here is the link about the Chinese version of this report.
Part1. What it can do.
This work has two parts:
- Transform interval max/min (for
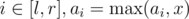 ) operations into interval add/subtract operations in O(1) or
) operations into interval add/subtract operations in O(1) or 
- Transform history max/min/sum queries into interval max/min operations in O(1).
Here are some sample problems I used in my report. At first you have a array A of length n and two auxiliary arrays B, C. Initially, B is equal to A and C is all zero.
Task 1. There are two kinds of operations:
- For all
 , change Ai to max(Ai, x)
, change Ai to max(Ai, x) - Query for the sum of Ai in [l, r]
It can be solved in 
Task 2. We can add more operations to Task 1:
- For all
 , change Ai to max(Ai, x)
, change Ai to max(Ai, x) - For all
 , change Ai to min(Ai, x)
, change Ai to min(Ai, x) - For all
 , change Ai to Ai + x, x can be a negative number
, change Ai to Ai + x, x can be a negative number - Query for the sum of Ai in [l, r]
It can be solved in  and I could not proved the exact time complexity yet, maybe It is still
and I could not proved the exact time complexity yet, maybe It is still  ;)
;)
Task 3. And we can query for some other things:
- For all
 , change Ai to max(Ai, x)
, change Ai to max(Ai, x) - For all
 , change Ai to min(Ai, x)
, change Ai to min(Ai, x) - For all
 , change Ai to Ai + x, x can be a negative number
, change Ai to Ai + x, x can be a negative number - Query for the sum of Bi in [l, r]
After each operation, for each i, if Ai changed in this operation, add 1 to Bi.
It’s time complexity is the same as Task 2.
Task 4. We can also deal with several arrays synchronously. Assume there are two arrays A1 and A2 of length n.
- For all
 , change Aa, i to min(Aa, i, x)
, change Aa, i to min(Aa, i, x) - For all
 , change Aa, i to Aa, i + x, x can be a negative number
, change Aa, i to Aa, i + x, x can be a negative number - Query for the max A1, i + A2, i in [l, r]
It can be solved in  and if there are k arrays, the time complexity will be raised to
and if there are k arrays, the time complexity will be raised to 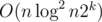 .
.
Task 5. And there are some tasks about historic information.
- For all
 , change Ai to Ai + x, x can be a negative number.
, change Ai to Ai + x, x can be a negative number. - Query for the sum of Bi in [l, r].
- Query for the sum of Ci in [l, r]
After each operation, for each i, change Bi to max(Bi, Ai) and add Ai to Ci.
The query for Bi can be solved in  and the query for Ci can be solved in
and the query for Ci can be solved in  .
.
Task 6. We can even merged the two parts together.
- For all
 , change Ai to max(Ai, x)
, change Ai to max(Ai, x) - For all
 , change Ai to Ai + x, x can be a negative number.
, change Ai to Ai + x, x can be a negative number. - Query for the sum of Bi in [l, r].
After each operation, for each i, change Bi to min(Bi, Ai).
It can be solved in 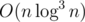 .
.
There are 11 sample tasks in my report and here are 6 of them. All of them are interesting and are hard to solve using the traditional techniques such as lazy tags.
Part2. The main idea
Interval min/max operations
To make the description clearer, I think it’s better to introduce an extended segment tree template.
I think most of the competitors’ templates of the lazy tag is like this ([l, r] is the node's interval and [ll, rr] is the operation's interval):
void modify(int node, int l, int r, int ll, int rr) {
if (l > rr || r < ll) return;
if (l >= ll && r <= rr) {
puttag(node); return;
}
pushdown(node);
int mid = (l + r) >> 1;
modify(node * 2, l, mid, ll, rr);
modify(node * 2 + 1, mid + 1, r, ll ,rr);
update();
}
The main idea is return whenever we can, put the tag whenever we can:
- When the operation's interval and the node's interval are no longer intersected, the information inside this subtree must not be affected. So we can return immediately.
- When the node's interval is contained by the operation's interval, all the information inside the subtree will be changed together. So we can put the tag on it and return.
In other words, we can replace the two conditions arbitrarily, i.e., we can extend the template like this:
void modify(int node, int l, int r, int ll, int rr) {
if (break_condition()) return;
if (tag_condition()) {
puttag(node); return;
}
pushdown(node);
int mid = (l + r) >> 1;
modify(node * 2, l, mid, ll, rr);
modify(node * 2 + 1, mid + 1, r, ll ,rr);
update();
}
What's the use of such a modification? In some advanced data structure tasks, it's impossible for us to put tags in such a weak condition l >= ll && r <= rr. But we can put it when the condition is stronger. We can use this template to deal with this kind of tasks but we need to analyze the time complexity carefully.
Simple task: There are three kinds of operations:
- For all
 , change Ai to
, change Ai to 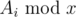
- For all
 , change Ai to x
, change Ai to x - Query for the sum of Ai in [l, r]
It's a classic problem (it's the simple extension of 438D - The Child and Sequence) and the traditional solution is to use balanced tree such as splay/treap to maintain the continuous segments with the same Ai and for operation 2, we find out all the segments with Ai ≥ x and change the value of each one.
But if we use segment tree, we can get a much simpler solution: let break_condition be l > rr || r < ll || max_value[node] < x and let tag_condition be l >= ll && r <= rr && max_value[node] == min_value[node]. And we can find that the time complexity of this segment tree is also  .
.
And now, we can easily describe the main idea of "segment tree beats". For each node, we maintain the maximum value max_value[node] and the strict second maximum value second_value[node].
When we are doing the interval min operation for number x. let break_condition be l > rr || r < ll || max_value[node] <= x and let tag_condition be l >= ll && r <= rr && second_value[node] < x. Under such an condition, after put this tag, all of the maximum values inside this subtree will be changed to x and they are still the maximum values of this subtree.
To make it easier to merge with other operations, we can maintain the values in this way: For each node, we maintain the maximum value inside this subtree and other values separately (the maximum values are the first kind and others are the second). Then, interval max operation will be changed to "add a number to the first kind values in some intervals". Keep the meanings of each kinds of values and the tags, you will find that the processes of pushdown and update will be much clearer.
That's the main idea of the first part of "segment tree beats". It is very simple, right? And it also has a very nice time complexity. (I will give out the proof of the time complexity in the third part of this article).
And let's see the first two sample tasks in part 1.
Task 1. In this task, we can maintain the number of the first kind of values inside each node t[node], and when we put tag "add x to the first kind values in this subtree", the sum will be added by t[node] * x. Then we can easily maintain the information we need.
Task 2. In this task, we can maintain the maximum values/ minimum values and others separately, i.e., there are three kinds of numbers now, and we will use three sets of tags for each kind of values. Also, to deal with the queries of the interval's sum, we need to maintain the numbers of the first kind and the second kind of values. Pay attention to some boundary conditions, if there are just two different values in this subtree, there will be no third kind of values and if all the values are the same, the set of the first kind and the second kind will be the same
Historic information
In this part, we will focus on three special values which I named "historic information":
- historic maximal value: after each operation, change Bi to max(Bi, Ai)
- historic minimal value: after each operation, change Bi to min(Bi, Ai)
- historic sum: after each operation, add Ci by Ai.
You may wonder why we need to consider these values. But in China, there had been several problems about these values before I wrote this report. And maintaining these values is a much harder task than it looks like. Here is a data structure task in Tsinghua University Training 2015:
Sample Task: Here is the link of this problem. There are five kinds of operations (x is a positive integer.):
- For all
 , change Ai to Ai + x.
, change Ai to Ai + x. - For all
 , change Ai to max(Ai - x, 0).
, change Ai to max(Ai - x, 0). - For all
 , change Ai to x.
, change Ai to x. - Query for Ai.
- Query for Bi.
After each operation, change Bi to max(Bi, Ai).
To solve this task, ordinary segment tree is enough. But It's not easy to deal with the relationship between the lazy tags and the historic information. I think it's a good sample problem to show the features of historic information.
We have already gotten the way to deal with the interval min/max operations. And they are good tools to maintain historic information.
Now, let use consider such a kind of problems (Part1. Task 5): interval add/subtract, query for the interval sum of historic information. It's quite hard since we can't just use the traditional lazy tag technique to solve it. But we can use an auxiliary array Di with the initial value of all zero to do some transformation:
- Historic maximal value: let Di = Bi - Ai. Then if we change Ai to Ai + x, Di will be changed to max(Di - x, 0).
- Historic minimal value: let Di = Bi - Ai. Then if we change Ai to Ai + x, Di will be changed to min(Di - x, 0).
- Historic sum: let Di = Ci - tAi while t is the current operation id. Then if we change Ai to Ai + x, Di will be changed to Di - (t - 1)x.
We can use the technique introduced in the previous part about interval min/max operations to maintain the sum of Di. And then we could get the sum of Bi or Ci.
What's more, since we have already transformed interval min/max operations to interval add/subtract operations, we can also maintain the interval sum of historic information under interval min/max operations (Part1. Task 6). This is a simple expansion and I think it's better to leave it as an exercise.
Part 3. The time complexity
In this part, I will give the proofs of the time complexity of Part 1 Task 1 and Part 1 Task 2. You can find that the proof of Task 2 is universal: it is equally applicable to Task 3 to Task 5. And Task 6 can be regarded as two layer nested “segment tree beats”. It's time complexity can be proved using the same way as Task 2.
Task 1
In this part, we will proof the algorithm showed in Part 2 of this problem is  : interval min operation, query for the interval sum.
: interval min operation, query for the interval sum.
gepardo has given a clear proof to show the time complexity of this problem is  in this comment. Here, I'd like to show another proof which is much more complex. But I think it is my closest attempt to proof Task 2 is
in this comment. Here, I'd like to show another proof which is much more complex. But I think it is my closest attempt to proof Task 2 is  . And this proof will show the relationship between "segment tree beats" and the solution of this problem given by xyz111 (you can find this solution in this website. The name of this problem is "Gorgeous Sequence" and the solution is written in English).
. And this proof will show the relationship between "segment tree beats" and the solution of this problem given by xyz111 (you can find this solution in this website. The name of this problem is "Gorgeous Sequence" and the solution is written in English).
The main idea is to transform max value into tags. Let the tag of each node in segment tree be the maximum value inside its interval. And if a node has the same tag as its father, we will remove the tag on it. Here is an simple example:
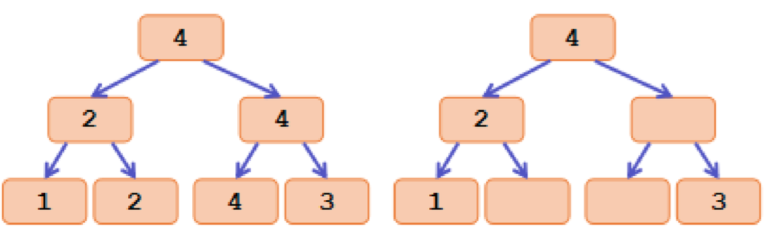
The left picture shows the maximum value of each node in a segment tree of array [1, 2, 4, 3]. And the left picture is the tags.
After the transformation, we can find that the strict second maximum value we maintained is just the maximum tag inside each subtree.
One important property of these tags is each tag is strictly greater than the tags inside its subtree. But why this property still holds after interval min operations? Consider the difference between this algorithm with the original segment tree: We will visit more nodes when second_value[node] >= x. This process ensure that we will put a tag only if all the tags inside this subtree is smaller than the new tag, i.e., we visit these large tags and delete them.
When do the tags change? One possibility is after an interval min operation, we will delete some tags and add some new tags. And another possibility is that if we just change some of the values inside the node, the previous tag may be pushed down after pushdown() (The maximum value of this subtree may be changed.)
For the convenience of description, let us define tag classes:
- All the tags added in the same interval min operation belong to the same tag class.
- After a pushdown, the new tag belongs to the same tag class as the old tag.
- Any two tags which do not satisfy above two conditions belong to different tag classes.
And we can divide the nodes we visit in a single interval min operation into two sets: ordinary nodes and extra nodes. Ordinary nodes are those nodes which an ordinary segment tree also visit in an operation of [l, r], and extra nodes are those nodes which we visit because the stronger break_condition.
Then, let w(T) (T is a tag class) be the number of nodes which has at least one tag in T inside its subtree, and let the potential function Φ(x) be the sum of w(T) for all existing T.
Since there are at most n tags in the segment tree, so the initial value of Φ(x) is  . Consider the influences to Φ(x):
. Consider the influences to Φ(x):
- After a
pushdown(), the old tag will be pushed down to two children ofnode, so Φ(x) will be increased by 2. - The new tag will occur on only ordinary nodes. So for the new tag class T, w(T) is
 . Since the number of ordinary nodes is
. Since the number of ordinary nodes is  .
. - The reason we visit an extra node is that we need to delete some tags inside its subtree. And a clear fact is that if we delete a tag in tag set T inside a subtree, all the tags in T inside this subtree will be also deleted. So, after visiting each extra node, Φ(x) will be subtract by at least 1.
Since the total increase of Φ(x) is  and each extra node will subtract 1 from Φ(x), we know that the time complexity is
and each extra node will subtract 1 from Φ(x), we know that the time complexity is  .
.
You may find that this potential function is just the same as the proof given by [usr:gepardo]. But using tags can bring us much more useful properties, and we can come up with some useful potential functions from the tags of which the definitions can be very strange if we want to define them just from the values. You may see it from the proof of the task 2.
Task 2
In this task, we will still use the tags defined in previous proof, and the potential function we choose is a little strange: let d(t) ( t is a tag ) be the depth of t in the segment tree and Φ(x) be the sum of d(t) for all existing tags. And since d(t) is  and the number of the tags is no more than n. So the initial value of Φ(x) is
and the number of the tags is no more than n. So the initial value of Φ(x) is  .
.
Then, let's consider the influences to Φ(x):
- After an interval min operation, there will be no tags on the extra nodes. So we can just consider
pushdownon ordinary nodes (For the interval add/subtract operations, we visit only ordinary nodes, so the following discussion is still correct) . And after apushdown, the old tag will be pushed down to the two children ofnode, and Φ(x) will be added by . Since there are
. Since there are  ordinary nodes,
ordinary nodes, pushdownwill make Φ(x) increased by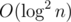 each interval min operation.
each interval min operation. - The new tag will occur on only ordinary nodes, so it will also make Φ(x) increased by
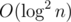 .
. - Each extra node will make Φ(x) decreased by 1 because there must be a tag deeper than this node which is deleted after this operation.
Since the total increase of Φ(x) is  and each extra node will subtract 1 from Φ(x), we prove that the time complexity is
and each extra node will subtract 1 from Φ(x), we prove that the time complexity is  .
.
What's more, in this proof, we do not use any special properties of interval add/subtract operation. So the proof is still hold for other operations. That's why I call this proof universal.
So far, this article is finished. I've never thought that it will be so popular. Thanks a lot for the encouragement and the support. I hope this article can help :)







