1043A — Elections
We can observe that result cannot exceed 201 — Awruk gets at least 101 votes from one person and Elodreip cannot get more than 100 votes from one person. So we can iterate over every possible integer from 1 to 201 and check if Awruk wins with k set to this integer. We have to remember that k — ai is always at least 0, so we have to check this condition too. Complexity O(n * M), where M denotes maximum possible value of ai. Try to solve it in O(n).
1043B — Lost Array
First, let's observe that we can replace array ai with array bi = ai - ai - 1, because all we care about are differences between neighboring elements. Now, we can see that our lost array can have length d if and only if for every j such that j + d ≤ n, bj = bj + d. So we can iterate over every possible d from 1 to n and check if it is correct in O(n). Complexity of whole algorithm is O(n2).
1043C — Smallest Word
Basically in problem we are given a word in which for every i we can reverse prefix of first i elements and we want to get the smallest lexicographically word. We will show that we can always achieve word in form ajbn - j.
Let's say that we solved our problem for prefix of length i and for this prefix we have word ajbi - j (at the beginning it's just empty word). If our next letter is b then we do nothing, because we will get word ajbi - j + 1 which is still the smallest lexicographically word. Otherwise we want to reverse prefix of length i, add letter a and reverse prefix of length i + 1, so we get a word aj + 1bi - j, which is still fine for us.
There is still a problem — what if we have already reversed prefix i and we just said that we will reverse it second time. But instead of reversing it second time, we can deny it's first reverse.
Final complexity is O(n).
1043D — Mysterious Crime
Deleting prefix and suffix is nothing more than taking a subarray. If subarray is common for all permutations then it has to appear in first permutation. We renumber all permutations such that first permutation is 1, 2, ..., n - 1, n.
Now for every i in every permutation we count how long is subarray starting at i which looks like i, i + 1, ..., i + k. It can be easily done in O(n) for one permutation with two pointers technique.
Now for every element i we compute reach$[i]$ equal the longest subarray starting in i which looks like i, i + 1, ..., i + k and it apears in all subarrays. It is just minimum over previously calculated values for all permutations.
Now we can see that our result is 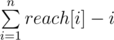 . Final complexity O(nm).
. Final complexity O(nm).
1043E — Train Hard, Win Easy
Let's compute result if there are no edges, we can add them later. If there are no edges then result for pair (i, j) is min(xi + yj, xj + yi). First let's fix i for which we want to compute result. Then calculate result with all pairs j such that xi + yj ≤ xj + yi. After some transformations we get that xi - yi ≤ xj - yj. Similarly we have that yi + xj < xi + yj if xi - yi > yj - xj.
So let's sort over differences of xi - yi and compute prefix sums of xi and suffix sums of yi. Now we can compute for every i result in O(1). Then we can iterate over every edge (u, v) and subtract min(xu + yv, xv + yu) from result of u and v.
Complexity O(nlogn).
1043F — Make It One
First let's observe that if there exists valid subset then it's size is at most 7 (because product of 7 smallest primes is bigger then 3 * 105). Let's define dp[i][j] — number of ways to pick i different elements such that their gcd is equal to j. We can use inclusion--exclusion principle to calculate it. Then dp[i][j] = 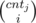 —
— 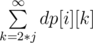 , where cntj denotes number of ai such that j | ai. Because for k > 3 * 105, dp[i][k] = 0 we have to check only k ≤ 3 * 105.
, where cntj denotes number of ai such that j | ai. Because for k > 3 * 105, dp[i][k] = 0 we have to check only k ≤ 3 * 105.
Our answer is the smallest i such that dp[i][1] is non-zero. Since dp[i][j] can be quite big we should compute it modulo some big prime.
Final complexity is O(logM * (n + M)), where M is equal to maximum of ai.





