1043A — Elections
We can observe that result cannot exceed 201 — Awruk gets at least 101 votes from one person and Elodreip cannot get more than 100 votes from one person. So we can iterate over every possible integer from 1 to 201 and check if Awruk wins with k set to this integer. We have to remember that k — ai is always at least 0, so we have to check this condition too. Complexity O(n * M), where M denotes maximum possible value of ai. Try to solve it in O(n).
#include <bits/stdc++.h>
using namespace std;
int n;
int mx = 0, sum = 0;
int main(){
scanf("%d", &n);
for(int i = 1; i <= n; ++i){
int a; scanf("%d", &a);
mx = max(mx, a);
sum += a;
}
sum *= 2;
sum += n;
sum /= n;
printf("%d", max(sum, mx));
return 0;
}
Author: Anadi
1043B — Lost Array
First, let's observe that we can replace array ai with array bi = ai - ai - 1, because all we care about are differences between neighboring elements. Now, we can see that our lost array can have length d if and only if for every j such that j + d ≤ n, bj = bj + d. So we can iterate over every possible d from 1 to n and check if it is correct in O(n). Complexity of whole algorithm is O(n2).
#include <bits/stdc++.h>
using namespace std;
const int N = 1007;
int n;
int in[N];
bool ok(int d){
for(int i = 0; i + d < n; ++i)
if(in[i + 1] - in[i] != in[i + d + 1] - in[i + d])
return false;
return true;
}
int main(){
scanf("%d", &n);
for(int i = 1; i <= n; ++i)
scanf("%d", &in[i]);
vector <int> res;
for(int i = 1; i <= n; ++i)
if(ok(i))
res.push_back(i);
printf("%d\n", res.size());
for(int v: res)
printf("%d ", v);
return 0;
}
Author: Anadi
1043C — Smallest Word
Basically in problem we are given a word in which for every i we can reverse prefix of first i elements and we want to get the smallest lexicographically word. We will show that we can always achieve word in form ajbn - j.
Let's say that we solved our problem for prefix of length i and for this prefix we have word ajbi - j (at the beginning it's just empty word). If our next letter is b then we do nothing, because we will get word ajbi - j + 1 which is still the smallest lexicographically word. Otherwise we want to reverse prefix of length i, add letter a and reverse prefix of length i + 1, so we get a word aj + 1bi - j, which is still fine for us.
There is still a problem — what if we have already reversed prefix i and we just said that we will reverse it second time. But instead of reversing it second time, we can deny it's first reverse.
Final complexity is O(n).
#include <bits/stdc++.h>
using namespace std;
const int N = 1007;
string s;
bool write[N];
int main(){
cin >> s;
for(int i = 1; i < s.size(); ++i)
if(s[i] == 'a'){
write[i - 1] ^= 1;
write[i] = 1;
}
for(int i = 0; i < s.size(); ++i)
printf("%d%c", write[i], i + 1 == (int)s.size() ? '\n' : ' ');
return 0;
}
Author: Anadi
1043D — Mysterious Crime
Deleting prefix and suffix is nothing more than taking a subarray. If subarray is common for all permutations then it has to appear in first permutation. We renumber all permutations such that first permutation is 1, 2, ..., n - 1, n.
Now for every i in every permutation we count how long is subarray starting at i which looks like i, i + 1, ..., i + k. It can be easily done in O(n) for one permutation with two pointers technique.
Now for every element i we compute reach[i] equal the longest subarray starting in i which looks like i, i + 1, ..., i + k and it apears in all subarrays. It is just minimum over previously calculated values for all permutations.
Now we can see that our result is 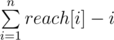 . Final complexity O(nm).
. Final complexity O(nm).
#include <bits/stdc++.h>
using namespace std;
typedef long long int LL;
const int N = 1e5 + 7;
int n, m;
int mn[N];
int ren[N];
int perm[15][N];
int main(){
scanf("%d %d", &n, &m);
for(int i = 1; i <= m; ++i)
for(int j = 1; j <= n; ++j)
scanf("%d", &perm[i][j]);
for(int i = 1; i <= n; ++i)
ren[perm[1][i]] = i;
for(int i = 1; i <= m; ++i)
for(int j = 1; j <= n; ++j)
perm[i][j] = ren[perm[i][j]];
for(int i = 1; i <= n; ++i)
mn[i] = n;
for(int i = 1; i <= m; ++i){
int cur = 1;
for(int j = 1; j <= n; ++j){
if(cur < j)
++cur;
while(cur < n && perm[i][cur + 1] == perm[i][cur] + 1)
++cur;
mn[perm[i][j]] = min(mn[perm[i][j]], perm[i][cur]);
}
}
LL res = 0;
int now = 1;
while(now <= n){
int cur = mn[now] - now + 1;
res += 1LL * (cur + 1) * cur / 2LL;
now = mn[now] + 1;
}
printf("%lld\n", res);
return 0;
}
Author: Anadi
1043E — Train Hard, Win Easy
Let's compute result if there are no edges, we can add them later. If there are no edges then result for pair (i, j) is min(xi + yj, xj + yi). First let's fix i for which we want to compute result. Then calculate result with all pairs j such that xi + yj ≤ xj + yi. After some transformations we get that xi - yi ≤ xj - yj. Similarly we have that yi + xj < xi + yj if xi - yi > yj - xj.
So let's sort over differences of xi - yi and compute prefix sums of xi and suffix sums of yi. Now we can compute for every i result in O(1). Then we can iterate over every edge (u, v) and subtract min(xu + yv, xv + yu) from result of u and v.
Complexity O(nlogn).
#include <bits/stdc++.h>
using namespace std;
typedef long long int LL;
#define st first
#define nd second
#define PII pair <int, int>
const int N = 3e5 + 7;
int n, m;
PII diff[N];
int place[N];
vector <int> G[N];
LL ans[N];
int x[N], y[N];
LL pref[N], suf[N];
int main(){
scanf("%d %d", &n, &m);
for(int i = 1; i <= n; ++i){
scanf("%d %d", &x[i], &y[i]);
diff[i] = {y[i] - x[i], i};
}
for(int i = 1; i <= m; ++i){
int u, v;
scanf("%d %d", &u, &v);
G[u].push_back(v);
G[v].push_back(u);
}
sort(diff + 1, diff + n + 1);
for(int i = 1; i <= n; ++i)
place[diff[i].nd] = i;
for(int i = 1; i <= n; ++i)
pref[i] = pref[i - 1] + y[diff[i].nd];
for(int i = n; i >= 1; --i)
suf[i] = suf[i + 1] + x[diff[i].nd];
for(int i = 1; i <= n; ++i){
int u = diff[i].nd;
LL res = pref[i - 1] + suf[i + 1] + 1LL * (i - 1) * x[u] + 1LL * (n - i) * y[u];
for(int v: G[u])
res -= min(x[u] + y[v], x[v] + y[u]);
ans[u] = res;
}
for(int i = 1; i <= n; ++i)
printf("%lld ", ans[i]);
return 0;
}
Author: Rzepa
1043F — Make It One
First let's observe that if there exists valid subset then it's size is at most 7 (because product of 7 smallest primes is bigger then 3 * 105). Let's define dp[i][j] — number of ways to pick i different elements such that their gcd is equal to j. We can use inclusion--exclusion principle to calculate it. Then dp[i][j] = 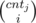 —
— 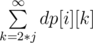 , where cntj denotes number of ai such that j | ai. Because for k > 3 * 105, dp[i][k] = 0 we have to check only k ≤ 3 * 105.
, where cntj denotes number of ai such that j | ai. Because for k > 3 * 105, dp[i][k] = 0 we have to check only k ≤ 3 * 105.
Our answer is the smallest i such that dp[i][1] is non-zero. Since dp[i][j] can be quite big we should compute it modulo some big prime.
Final complexity is O(logM * (n + M)), where M is equal to maximum of ai.
#include <bits/stdc++.h>
using namespace std;
const int N = 3e5 + 7;
const int MX = 1e9 + 7;
int n;
int cnt[N];
int sil[N];
int odw[N];
int dp[20][N];
int fast(int a, int b){
int ret = 1;
while(b){
if(b & 1)
ret = (1LL * ret * a)%MX;
b >>= 1;
a = (1LL * a * a)%MX;
}
return ret;
}
int newton(int a, int b){
if(b < 0 || a < b) return 0;
return (((1LL * sil[a] * odw[b])%MX) * odw[a - b])%MX;
}
void sub(int &a, int b){
a -= b;
if(a < 0)
a += MX;
}
int main(){
sil[0] = 1;
for(int i = 1; i < N; ++i)
sil[i] = (1LL * sil[i - 1] * i)%MX;
odw[N - 1] = fast(sil[N - 1], MX - 2);
for(int i = N - 1; i >= 1; --i)
odw[i - 1] = (1LL * odw[i] * i)%MX;
scanf("%d", &n);
for(int i = 1; i <= n; ++i){
int a;
scanf("%d", &a);
cnt[a]++;
}
for(int i = 1; i < N; ++i)
for(int j = i + i; j < N; j += i)
cnt[i] += cnt[j];
for(int i = 1; i < 20; ++i){
for(int j = N - 1; j >= 1; --j){
dp[i][j] = newton(cnt[j], i);
for(int k = j + j; k < N; k += j)
sub(dp[i][j], dp[i][k]);
}
if(dp[i][1] > 0){
printf("%d\n", i);
return 0;
}
}
puts("-1");
return 0;
}
#include <bits/stdc++.h>
using namespace std;
const int N = 3e5 + 7;
int n;
int cnt[N];
int roz[N];
int dist[N];
queue <int> Q;
vector <int> dv[N];
int base(int a){
int ret = 1;
while(a > 1){
if(ret%roz[a] != 0)
ret *= roz[a];
a /= roz[a];
}
return ret;
}
void getEdges(int u, int d){
vector <int> cur;
vector <int> val;
while(u > 1){
cur.push_back(roz[u]);
u /= roz[u];
}
for(int v: cur)
u *= v;
int T = 1 << (int)cur.size();
val.resize(T);
for(int i = 0; i < T; ++i){
val[i] = u;
for(int j = 0; j < (int)cur.size(); ++j)
if(i & (1 << j))
val[i] /= cur[j];
}
for(int i = 0; i < T; ++i){
int s = 0;
for(int j = i; true; j = (j - 1) & i){
if(__builtin_popcount(i ^ j) & 1)
s -= cnt[val[j]];
else
s += cnt[val[j]];
if(j == 0)
break;
}
assert(s >= 0);
if(s && dist[val[i]] == -1){
dist[val[i]] = d;
Q.push(val[i]);
}
}
}
int main(){
scanf("%d", &n);
for(int i = 2; i < N; ++i){
if(roz[i] != 0)
continue;
for(int j = i; j < N; j += i)
roz[j] = i;
}
for(int i = 1; i < N; ++i)
for(int j = i; j < N; j += i)
dv[j].push_back(i);
for(int i = 1; i < N; ++i)
dist[i] = -1;
for(int i = 1; i <= n; ++i){
int a;
scanf("%d", &a);
a = base(a);
if(dist[a] != -1)
continue;
dist[a] = 1;
Q.push(a);
for(int v: dv[a])
cnt[v]++;
}
while(!Q.empty()){
int u = Q.front();
Q.pop();
getEdges(u, dist[u] + 1);
}
printf("%d\n", dist[1]);
return 0;
}
Author: Anadi
1043G — Speckled Band
Let's solve the problem for some string s for any time.
Let's say, that partition of string s into k strings s1s2... si1, si1 + 1... si2, ..., {sik - 1 + 1}... sik is good if at least one pair of this strings are equal. We want to find a minimal possible number of different strings in all good partitions.
It's easy to see, that the answer is - 1 if and only if all symbols in s are different. And if we have two equal symbols si = sj (i < j) we can cut a string into strings s1... si - 1, si, si + 1... sj - 1, sj, sj + 1... sn and it is a good partition. In this partition there is at most 4 different strings.
So the answer can be - 1, 1, 2, 3, 4.
The answer is - 1 if all symbols in s are different (case 0).
The answer is 1 if the string s = aaa... a, for some string a (case 1).
The answer is 2 if the string s is aab, aba or baa for some strings a and b (case 2).
The answer is 3 if the string s is baac, bcaa or aabc for some strings a, b, c. In two last cases it's easy to see, that |a| = 1 (case 3).
To solve our problem let's build suffix array with lcp for string s. And let's find lti~--- minimal possible number r, such that sisi + 1... sr is a tandem (the string, that can be presented as aa for some string a) and rti~--- maximal possible number l such that slsl + 1... si is a tandem. This numbers can be found using Main and Lorentz algorithm for finding tandem repetitions in the string.
Now we can solve query for segment [l, r]: \begin{itemize} \item Case 0: if r - l ≥ 26, there exists equal symbols, otherwise we can check it by O(r - l); \item Case 1: to check that s[l... r] = aa... a we can see that |a| is a divisor of (r - l + 1) and (r - l + 1) / |a| is a prime number (if we take a longest possible string a). So we should check only O(log(n)) lenghts of string a; \item Case 2: s = aab  ltl ≤ r, s = baa
ltl ≤ r, s = baa  rtr ≥ l. In the last case we should check, that s[l... r] has a border. It's the most interesting part of the problem, let's solve it in the end; \item Case 3: s = abac
rtr ≥ l. In the last case we should check, that s[l... r] has a border. It's the most interesting part of the problem, let's solve it in the end; \item Case 3: s = abac  sl exists on sl + 1... sr (can be done using prefix sums), s = baca
sl exists on sl + 1... sr (can be done using prefix sums), s = baca  sr exists on sl... sr - 1 (can be done using prefix sums). To check s = baac we can check, that lti ≤ r for some l ≤ i ≤ r, that can be done using minimum on segment in the array lt. \end{itemize}
sr exists on sl... sr - 1 (can be done using prefix sums). To check s = baac we can check, that lti ≤ r for some l ≤ i ≤ r, that can be done using minimum on segment in the array lt. \end{itemize}
Now we should the hardest part of this problem~--- we have some segments [l, r]. For all of them, we should check that the border of s[l... r] exists. Here I know two methods, that uses only suffix array. Easiest of them:
We have segment [l, r]. Let's check for all lengths 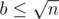 , that s[l... (l + b - 1)] = s[(r - b + 1)... r]. If we don't find border, if it exists, it's length
, that s[l... (l + b - 1)] = s[(r - b + 1)... r]. If we don't find border, if it exists, it's length 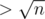 . Let's define i~--- maximal index i such that lcp(l, i) ≥ r - i + 1, and string s[i... r] is a border of s[l... r]. So
. Let's define i~--- maximal index i such that lcp(l, i) ≥ r - i + 1, and string s[i... r] is a border of s[l... r]. So 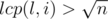 . But it's easy to see, that the distance between l and i in suffix array
. But it's easy to see, that the distance between l and i in suffix array 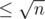 , so we need to check only
, so we need to check only  variants of i.
variants of i.
Another method can check that border exists for all segments [l, r] using offline algorithm by O(q·log(n)2) time.
So the total complexity will be 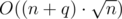 or O((n + q)·log(n)2).
or O((n + q)·log(n)2).
#include <bits/stdc++.h>
using namespace std;
const int BIG = 1e9 + 239;
const int M = 2 * 1e5 + 239;
const int L = 19;
const int A = 30;
const int T = (1 << 19);
const int two = 2;
int flm[two][M];
inline void z_function(string &s, int c)
{
int n = s.length();
flm[c][0] = 0;
int l = 0;
int r = 0;
for (int i = 1; i < n; i++)
{
flm[c][i] = min(flm[c][i - l], r - i);
if (flm[c][i] < 0) flm[c][i] = 0;
while (i + flm[c][i] < n && s[flm[c][i]] == s[i + flm[c][i]]) flm[c][i]++;
if (i + flm[c][i] > r)
{
l = i;
r = i + flm[c][i];
}
}
}
int a[M], lcp[M], pos[M];
inline void suffix_array(string s)
{
s += (char)(31);
int n = s.length();
vector<pair<char, int> > v;
for (int i = 0; i < n; i++)
v.push_back(make_pair(s[i], i));
sort(v.begin(), v.end());
vector<pair<int, int> > num;
int last = 0;
for (int i = 0; i < n - 1; i++)
{
num.push_back(make_pair(last, v[i].second));
if (v[i].first != v[i + 1].first) last++;
}
num.push_back(make_pair(last, v.back().second));
vector<int> u(n);
for (int i = 0; i < n; i++) u[num[i].second] = num[i].first;
int d = 1;
vector<pair<pair<int, int>, int> > t;
vector<vector<pair<int, int> > > h;
while (d < n)
{
t.clear();
h.clear();
h.resize(n);
for (int i = 0; i < n; i++)
{
int l = num[i].second - d;
if (l < 0) l += n;
h[u[l]].push_back(make_pair(num[i].first, l));
}
for (int i = 0; i < n; i++)
for (pair<int, int> r : h[i])
t.push_back(make_pair(make_pair(i, r.first), r.second));
last = 0;
num.clear();
for (int i = 0; i < n - 1; i++)
{
num.push_back(make_pair(last, t[i].second));
if (t[i].first != t[i + 1].first) last++;
}
num.push_back(make_pair(last, t.back().second));
for (int i = 0; i < n; i++) u[num[i].second] = num[i].first;
d <<= 1;
}
for (int i = 1; i < n; i++) a[i - 1] = num[i].second;
}
string s;
inline void kasai()
{
int n = s.size();
suffix_array(s);
for (int i = 0; i < n; i++)
pos[a[i]] = i;
int k = 0;
for (int i = 0; i < n; i++)
{
if (pos[i] == n - 1) continue;
while (s[i + k] == s[a[pos[i] + 1] + k] && a[pos[i] + 1] + k < n && i + k < n) k++;
lcp[pos[i]] = k;
k = max(0, k - 1);
}
}
int n, lw[M], rw[M];
string prr, rvl;
vector<int> open_l[M], close_l[M];
vector<int> open_r[M], close_r[M];
multiset<int> nw;
inline void func(int l, int r)
{
if (r - l == 1) return;
int mid = (l + r) >> 1;
func(l, mid);
func(mid, r);
rvl = "";
for (int i = mid - 1; i >= l; i--) rvl += s[i];
z_function(rvl, 0);
prr = "";
for (int i = mid; i < r; i++) prr += s[i];
prr += '#';
for (int i = l; i < mid; i++) prr += s[i];
z_function(prr, 1);
for (int c = l; c < mid; c++)
{
int k1 = 0;
if (c > l) k1 = flm[0][mid - c];
int k2 = flm[1][r - mid + 1 + c - l];
int len = mid - c;
int lg = max(len - k2, 0);
int rg = min(len - 1, k1);
if (rg >= lg)
{
open_l[c - rg].push_back((2 * len));
close_l[c - lg].push_back((2 * len));
open_r[c - rg + 2 * len - 1].push_back((2 * len));
close_r[c - lg + 2 * len - 1].push_back((2 * len));
}
}
rvl = "";
for (int i = mid; i < r; i++) rvl += s[i];
z_function(rvl, 0);
prr = "";
for (int i = mid - 1; i >= l; i--) prr += s[i];
prr += '#';
for (int i = r - 1; i >= mid; i--) prr += s[i];
z_function(prr, 1);
for (int c = mid; c < r; c++)
{
int k1 = 0;
if (c != r - 1) k1 = flm[0][c + 1 - mid];
int k2 = flm[1][r - c + mid - l];
int len = c - mid + 1;
int lg = max(len - k2, 0);
int rg = min(len - 1, k1);
if (rg >= lg)
{
open_l[c + lg - 2 * len + 1].push_back((2 * len));
close_l[c + rg - 2 * len + 1].push_back((2 * len));
open_r[c + lg].push_back((2 * len));
close_r[c + rg].push_back((2 * len));
}
}
for (int i = l; i < r; i++)
{
for (int len : open_l[i]) nw.insert(len);
if (!nw.empty()) lw[i] = min(lw[i], *nw.begin());
for (int len : close_l[i]) nw.erase(nw.lower_bound(len));
open_l[i].clear();
close_l[i].clear();
}
for (int i = l; i < r; i++)
{
for (int len : open_r[i]) nw.insert(len);
if (!nw.empty()) rw[i] = min(rw[i], *nw.begin());
for (int len : close_r[i]) nw.erase(nw.lower_bound(len));
open_r[i].clear();
close_r[i].clear();
}
}
int mn[L][M], st2[M], lc[L][M], kol[A][M];
inline int getmin(int l, int r)
{
int u = st2[r - l + 1];
return min(mn[u][l], mn[u][r - (1 << u) + 1]);
}
inline int gett(int l, int r)
{
if (l == r) return (n - l);
l = pos[l];
r = pos[r];
if (l > r) swap(l, r);
r--;
int u = st2[r - l + 1];
return min(lc[u][l], lc[u][r - (1 << u) + 1]);
}
int q, la[M], ra[M], has[M], mnp[M];
inline void init()
{
for (int i = 0; i < n; i++) mn[0][i] = lw[i];
for (int i = 0; i < n - 1; i++) lc[0][i] = lcp[i];
for (int i = 1; i < L; i++)
for (int j = 0; j < n; j++)
{
int r = (j + (1 << (i - 1)));
if (r >= n)
{
mn[i][j] = mn[i - 1][j];
continue;
}
mn[i][j] = min(mn[i - 1][j], mn[i - 1][r]);
}
for (int i = 1; i < L; i++)
for (int j = 0; j < n - 1; j++)
{
int r = (j + (1 << (i - 1)));
if (r >= n - 1)
{
lc[i][j] = lc[i - 1][j];
continue;
}
lc[i][j] = min(lc[i - 1][j], lc[i - 1][r]);
}
st2[1] = 0;
for (int i = 2; i <= n; i++)
{
st2[i] = st2[i - 1];
if ((1 << (st2[i] + 1)) <= i) st2[i]++;
}
}
int in[L][M], gl[T];
inline void build(int i, int l, int r)
{
if (i == 0) gl[i] = 0;
else gl[i] = gl[(i - 1) / 2] + 1;
if (r - l == 1)
{
in[gl[i]][l] = a[l];
return;
}
int mid = (l + r) >> 1;
build(2 * i + 1, l, mid);
build(2 * i + 2, mid, r);
merge(in[gl[i] + 1] + l, in[gl[i] + 1] + mid, in[gl[i] + 1] + mid, in[gl[i] + 1] + r, in[gl[i]] + l);
}
inline bool is_on(int i, int l, int r, int ql, int qr, int xl, int xr)
{
if (r <= ql || qr <= l) return false;
if (ql <= l && r <= qr)
{
int it = upper_bound(in[gl[i]] + l, in[gl[i]] + r, xl) - in[gl[i]] - l;
if (it == r - l) return false;
return (in[gl[i]][it + l] <= xr);
}
int mid = (l + r) >> 1;
if (is_on(2 * i + 1, l, mid, ql, qr, xl, xr)) return true;
return is_on(2 * i + 2, mid, r, ql, qr, xl, xr);
}
inline bool check_all(int l, int r)
{
int len = (r - l + 1);
int pl = pos[l];
int lf = pl;
int rf = n;
while (rf - lf > 1)
{
int h = (lf + rf) / 2;
if (gett(a[h], l) >= len) lf = h;
else rf = h;
}
int rg = lf + 1;
lf = -1;
rf = pl;
while (rf - lf > 1)
{
int h = (lf + rf) / 2;
if (gett(a[h], l) >= len) rf = h;
else lf = h;
}
int lg = rf;
return is_on(0, 0, n, lg, rg, l, r);
}
int par[M];
set<int> cmp[M];
set<pair<int, int> > sc[M];
vector<int> ok[M];
vector<pair<int, int> > mg[M];
inline void border_check()
{
for (int i = 0; i < q; i++) has[i] = false;
for (int i = 0; i < q; i++) ok[ra[i] - la[i]].push_back(i);
for (int i = 0; i < n - 1; i++) mg[lcp[i]].push_back(make_pair(a[i], a[i + 1]));
for (int i = 0; i < n; i++)
{
par[i] = i;
cmp[i].insert(i);
}
for (int c = n; c >= 1; c--)
{
for (int i : ok[c - 1])
sc[par[la[i]]].insert(make_pair(ra[i], i));
for (pair<int, int> t : mg[c])
{
int l = par[t.first];
int r = par[t.second];
if (cmp[l].size() > cmp[r].size()) swap(l, r);
for (int x : cmp[l])
while (true)
{
auto it = sc[r].lower_bound(make_pair(x, 0));
if (it == sc[r].end() || it->first > x + c - 1) break;
has[it->second] = true;
sc[r].erase(it);
}
for (pair<int, int> u : sc[l])
{
int id = u.second;
auto uk = cmp[r].lower_bound(ra[id] - c + 1);
if (uk != cmp[r].end() && (*uk) <= ra[id])
has[id] = true;
else
sc[r].insert(u);
}
for (int x : cmp[l])
{
par[x] = r;
cmp[r].insert(x);
}
}
}
for (int i = 0; i < q; i++)
if (!has[i] && check_all(la[i], ra[i]))
{
has[i] = true;
continue;
}
}
inline bool checkno(int l, int r)
{
if (r - l + 1 > 26) return false;
vector<int> kol(26, 0);
for (int x = l; x <= r; x++)
{
if (kol[s[x] - 'a'] > 0) return false;
kol[s[x] - 'a']++;
}
return true;
}
inline bool try_kol(int l, int r, int p)
{
int len = (r - l + 1) / p;
return (gett(l, l + len) >= (r - l + 1 - len));
}
inline bool ison(int l, int r, char x)
{
return (kol[x - 'a'][r + 1] > kol[x - 'a'][l]);
}
inline int query(int l, int r, int id)
{
if (checkno(l, r)) return -1;
int len = (r - l + 1);
while (len > 1)
{
int p = mnp[len];
if (try_kol(l, r, p)) return 1;
while ((len % p) == 0) len /= p;
}
if (lw[l] <= r) return 2;
if (rw[r] >= l) return 2;
if (has[id]) return 2;
if (ison(l + 1, r, s[l])) return 3;
if (ison(l, r - 1, s[r])) return 3;
if (getmin(l, r) <= r) return 3;
return 4;
}
int main()
{
cin.sync_with_stdio(0);
cin >> n >> s;
memset(mnp, -1, sizeof(mnp));
for (int i = 2; i <= n; i++)
if (mnp[i] == -1)
for (int j = i; j <= n; j += i)
if (mnp[j] == -1)
mnp[j] = i;
memset(kol[0], 0, sizeof(kol[0]));
for (int i = 0; i < n; i++)
{
for (int x = 0; x < 26; x++) kol[x][i + 1] = kol[x][i];
kol[s[i] - 'a'][i + 1]++;
}
for (int i = 0; i < n; i++)
{
lw[i] = n + 1;
rw[i] = n + 1;
}
func(0, n);
for (int i = 0; i < n; i++)
{
if (lw[i] == n + 1) lw[i] = n;
else lw[i] += (i - 1);
if (rw[i] == n + 1) rw[i] = -1;
else rw[i] = (i - rw[i] + 1);
}
kasai();
init();
build(0, 0, n);
cin >> q;
for (int i = 0; i < q; i++)
{
cin >> la[i] >> ra[i];
la[i]--, ra[i]--;
}
border_check();
for (int i = 0; i < q; i++) cout << query(la[i], ra[i], i) << "\n";
return 0;
}
#include <bits/stdc++.h>
using namespace std;
#define TIME (clock() * 1.0 / CLOCKS_PER_SEC)
const int BIG = 1e9 + 239;
const int M = 2 * 1e5 + 239;
const int L = 19;
const int A = 30;
const int T = (1 << 19);
const int two = 2;
int flm[two][M];
inline void z_function(string &s, int c)
{
int n = s.length();
flm[c][0] = 0;
int l = 0;
int r = 0;
for (int i = 1; i < n; i++)
{
flm[c][i] = min(flm[c][i - l], r - i);
if (flm[c][i] < 0) flm[c][i] = 0;
while (i + flm[c][i] < n && s[flm[c][i]] == s[i + flm[c][i]]) flm[c][i]++;
if (i + flm[c][i] > r)
{
l = i;
r = i + flm[c][i];
}
}
}
int a[M], lcp[M], pos[M];
inline void suffix_array(string s)
{
s += (char)(31);
int n = s.length();
vector<pair<char, int> > v;
for (int i = 0; i < n; i++)
v.push_back(make_pair(s[i], i));
sort(v.begin(), v.end());
vector<pair<int, int> > num;
int last = 0;
for (int i = 0; i < n - 1; i++)
{
num.push_back(make_pair(last, v[i].second));
if (v[i].first != v[i + 1].first) last++;
}
num.push_back(make_pair(last, v.back().second));
vector<int> u(n);
for (int i = 0; i < n; i++) u[num[i].second] = num[i].first;
int d = 1;
vector<pair<pair<int, int>, int> > t;
vector<vector<pair<int, int> > > h;
while (d < n)
{
t.clear();
h.clear();
h.resize(n);
for (int i = 0; i < n; i++)
{
int l = num[i].second - d;
if (l < 0) l += n;
h[u[l]].push_back(make_pair(num[i].first, l));
}
for (int i = 0; i < n; i++)
for (pair<int, int> r : h[i])
t.push_back(make_pair(make_pair(i, r.first), r.second));
last = 0;
num.clear();
for (int i = 0; i < n - 1; i++)
{
num.push_back(make_pair(last, t[i].second));
if (t[i].first != t[i + 1].first) last++;
}
num.push_back(make_pair(last, t.back().second));
for (int i = 0; i < n; i++) u[num[i].second] = num[i].first;
d <<= 1;
}
for (int i = 1; i < n; i++) a[i - 1] = num[i].second;
}
string s;
inline void kasai()
{
int n = s.size();
suffix_array(s);
for (int i = 0; i < n; i++)
pos[a[i]] = i;
int k = 0;
for (int i = 0; i < n; i++)
{
if (pos[i] == n - 1) continue;
while (s[i + k] == s[a[pos[i] + 1] + k] && a[pos[i] + 1] + k < n && i + k < n) k++;
lcp[pos[i]] = k;
k = max(0, k - 1);
}
}
int n, lw[M], rw[M];
string prr, rvl;
vector<int> open_l[M], close_l[M];
vector<int> open_r[M], close_r[M];
multiset<int> nw;
inline void func(int l, int r)
{
if (r - l == 1) return;
int mid = (l + r) >> 1;
func(l, mid);
func(mid, r);
rvl = "";
for (int i = mid - 1; i >= l; i--) rvl += s[i];
z_function(rvl, 0);
prr = "";
for (int i = mid; i < r; i++) prr += s[i];
prr += '#';
for (int i = l; i < mid; i++) prr += s[i];
z_function(prr, 1);
for (int c = l; c < mid; c++)
{
int k1 = 0;
if (c > l) k1 = flm[0][mid - c];
int k2 = flm[1][r - mid + 1 + c - l];
int len = mid - c;
int lg = max(len - k2, 0);
int rg = min(len - 1, k1);
if (rg >= lg)
{
open_l[c - rg].push_back((2 * len));
close_l[c - lg].push_back((2 * len));
open_r[c - rg + 2 * len - 1].push_back((2 * len));
close_r[c - lg + 2 * len - 1].push_back((2 * len));
}
}
rvl = "";
for (int i = mid; i < r; i++) rvl += s[i];
z_function(rvl, 0);
prr = "";
for (int i = mid - 1; i >= l; i--) prr += s[i];
prr += '#';
for (int i = r - 1; i >= mid; i--) prr += s[i];
z_function(prr, 1);
for (int c = mid; c < r; c++)
{
int k1 = 0;
if (c != r - 1) k1 = flm[0][c + 1 - mid];
int k2 = flm[1][r - c + mid - l];
int len = c - mid + 1;
int lg = max(len - k2, 0);
int rg = min(len - 1, k1);
if (rg >= lg)
{
open_l[c + lg - 2 * len + 1].push_back((2 * len));
close_l[c + rg - 2 * len + 1].push_back((2 * len));
open_r[c + lg].push_back((2 * len));
close_r[c + rg].push_back((2 * len));
}
}
for (int i = l; i < r; i++)
{
for (int len : open_l[i]) nw.insert(len);
if (!nw.empty()) lw[i] = min(lw[i], *nw.begin());
for (int len : close_l[i]) nw.erase(nw.lower_bound(len));
open_l[i].clear();
close_l[i].clear();
}
for (int i = l; i < r; i++)
{
for (int len : open_r[i]) nw.insert(len);
if (!nw.empty()) rw[i] = min(rw[i], *nw.begin());
for (int len : close_r[i]) nw.erase(nw.lower_bound(len));
open_r[i].clear();
close_r[i].clear();
}
}
int mn[L][M], st2[M], lc[L][M], kol[A][M];
inline int getmin(int l, int r)
{
int u = st2[r - l + 1];
return min(mn[u][l], mn[u][r - (1 << u) + 1]);
}
inline int gett(int l, int r)
{
if (l == r) return (n - l);
l = pos[l];
r = pos[r];
if (l > r) swap(l, r);
r--;
int u = st2[r - l + 1];
return min(lc[u][l], lc[u][r - (1 << u) + 1]);
}
int q, mnp[M];
inline void init()
{
for (int i = 0; i < n; i++) mn[0][i] = lw[i];
for (int i = 0; i < n - 1; i++) lc[0][i] = lcp[i];
for (int i = 1; i < L; i++)
for (int j = 0; j < n; j++)
{
int r = (j + (1 << (i - 1)));
if (r >= n)
{
mn[i][j] = mn[i - 1][j];
continue;
}
mn[i][j] = min(mn[i - 1][j], mn[i - 1][r]);
}
for (int i = 1; i < L; i++)
for (int j = 0; j < n - 1; j++)
{
int r = (j + (1 << (i - 1)));
if (r >= n - 1)
{
lc[i][j] = lc[i - 1][j];
continue;
}
lc[i][j] = min(lc[i - 1][j], lc[i - 1][r]);
}
st2[1] = 0;
for (int i = 2; i <= n; i++)
{
st2[i] = st2[i - 1];
if ((1 << (st2[i] + 1)) <= i) st2[i]++;
}
}
int u, len;
inline bool check(int l, int r)
{
for (int t = 1; t <= min(len, ((r - l + 1) / 2)); t++)
if (gett(l, r - t + 1) >= t)
return true;
for (int i = max(0, pos[l] - len); i <= min(n - 1, pos[l] + len); i++)
if (l < a[i] && a[i] <= r && gett(l, a[i]) >= r - a[i] + 1)
return true;
return false;
}
inline bool checkno(int l, int r)
{
if (r - l + 1 > 26) return false;
vector<int> kol(26, 0);
for (int x = l; x <= r; x++)
{
if (kol[s[x] - 'a'] > 0) return false;
kol[s[x] - 'a']++;
}
return true;
}
inline bool try_kol(int l, int r, int p)
{
int len = (r - l + 1) / p;
return (gett(l, l + len) >= (r - l + 1 - len));
}
inline bool ison(int l, int r, char x)
{
return (kol[x - 'a'][r + 1] > kol[x - 'a'][l]);
}
inline int query(int l, int r)
{
if (checkno(l, r)) return -1;
int len = (r - l + 1);
while (len > 1)
{
int p = mnp[len];
if (try_kol(l, r, p)) return 1;
while ((len % p) == 0) len /= p;
}
if (lw[l] <= r) return 2;
if (rw[r] >= l) return 2;
if (check(l, r)) return 2;
if (ison(l + 1, r, s[l])) return 3;
if (ison(l, r - 1, s[r])) return 3;
if (getmin(l, r) <= r) return 3;
return 4;
}
int main()
{
cin.sync_with_stdio(0);
cin >> n >> s;
memset(mnp, -1, sizeof(mnp));
for (int i = 2; i <= n; i++)
if (mnp[i] == -1)
for (int j = i; j <= n; j += i)
if (mnp[j] == -1)
mnp[j] = i;
memset(kol[0], 0, sizeof(kol[0]));
for (int i = 0; i < n; i++)
{
for (int x = 0; x < 26; x++) kol[x][i + 1] = kol[x][i];
kol[s[i] - 'a'][i + 1]++;
}
for (int i = 0; i < n; i++)
{
lw[i] = n + 1;
rw[i] = n + 1;
}
func(0, n);
for (int i = 0; i < n; i++)
{
if (lw[i] == n + 1) lw[i] = n;
else lw[i] += (i - 1);
if (rw[i] == n + 1) rw[i] = -1;
else rw[i] = (i - rw[i] + 1);
}
kasai();
init();
cin >> q;
for (int i = 0; i < n; i++)
if (i * i >= n)
{
len = i + 3;
break;
}
for (int i = 0; i < q; i++)
{
int l, r;
cin >> l >> r;
l--, r--;
cout << query(l, r) << "\n";
}
return 0;
}
Author: isaf27





