TL;DR This article features Modular class which can be conviniently used for modular arithmetic more "naturally".
Motivation
Recent round featured an interesting problem 1081C - Colorful Bricks (if you plan to solve it, read this later). Combinatoric solution requires you to calculate:
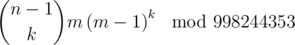
Many contestants failed pretest because of missing modulo operation somewhere in code.
Solution
Many contestants use functions like add(ll a, ll b) or mul(ll a , ll b) which makes implementation somewhat clumsy.
I present you an alternate approach using Modular class.
template <int MOD=998'244'353>
struct Modular {
int value;
static const int MOD_value = MOD;
Modular(long long v = 0) { value = v % MOD; if (value < 0) value += MOD;}
Modular(long long a, long long b) : value(0){ *this += a; *this /= b;}
Modular& operator+=(Modular const& b) {value += b.value; if (value >= MOD) value -= MOD; return *this;}
Modular& operator-=(Modular const& b) {value -= b.value; if (value < 0) value += MOD;return *this;}
Modular& operator*=(Modular const& b) {value = (long long)value * b.value % MOD;return *this;}
friend Modular mexp(Modular a, long long e) {
Modular res = 1; while (e) { if (e&1) res *= a; a *= a; e >>= 1; }
return res;
}
friend Modular inverse(Modular a) { return mexp(a, MOD - 2); }
Modular& operator/=(Modular const& b) { return *this *= inverse(b); }
friend Modular operator+(Modular a, Modular const b) { return a += b; }
friend Modular operator-(Modular a, Modular const b) { return a -= b; }
friend Modular operator-(Modular const a) { return 0 - a; }
friend Modular operator*(Modular a, Modular const b) { return a *= b; }
friend Modular operator/(Modular a, Modular const b) { return a /= b; }
friend std::ostream& operator<<(std::ostream& os, Modular const& a) {return os << a.value;}
friend bool operator==(Modular const& a, Modular const& b) {return a.value == b.value;}
friend bool operator!=(Modular const& a, Modular const& b) {return a.value != b.value;}
};
Using this code can be written more naturally in modular field just like in integer field. This implementation simplifies usage, for example:
// Chained Multiplication or Successive Simple Multiplication
Modular<998244353> a=1, m=123456789;
a *= m * m * m; // a = 519994069
// Inverse
a=inverse(m) // a=25170271
// fractions
Modular<> frac=(1,2); // frac=1*2^(-1) % 998244353 = 499122177
// Modular exponentiation
Modular<> power(2);
power=mexp(power,500); // power = 616118644
Credits to Jakube and here's the link to original source. Link: Modular.h






