Since its data has been lost during the dark days of Codeforces, no version of it has been re-released, and I feel the round itself is quite educational, so I decided to give a try.
390A - Inna and Alarm Clock
The criterion shows that we can only use either vertical segments or horizontal segments.
Since there is no limit on the segments' length, we can see that it's always optimal to use a segment with infinite length (or may be known as a line).
We can see that the vertical line x = a will span through every alarm clocks standing at positions with x-coordinate being equal to a. In a similar manner, the horizontal line y = b will span through every alarm clocks standing at positions with y-coordinate being equal to b.
So, if we use vertical lines, the number of segments used will be the number of distinct values of x-coordinates found in the data. Similarly, the number of horizontal segments used will be the number of distinct values of y-coordinates found.
The process can be implemented by a counting array, or a map.
Time complexity: 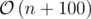 for regular arrays, or
for regular arrays, or 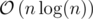 for maps.
for maps.
Submission link: 48211481
#pragma GCC optimize("Ofast")
#include <bits/stdc++.h>
using namespace std;
#define endl '\n'
mt19937 rng32(chrono::steady_clock::now().time_since_epoch().count());
mt19937_64 rng64(chrono::steady_clock::now().time_since_epoch().count());
int main(int argc, char* argv[]) {
ios_base::sync_with_stdio(0); cin.tie(NULL);
int n; cin >> n;
map<int, int> cntx, cnty;
while (n--) {
int x, y;
cin >> x >> y;
cntx[x]++; cnty[y]++;
}
cout << min(cntx.size(), cnty.size()) << endl;
return 0;
}
Submission link: 48211597
#pragma GCC optimize("Ofast")
#include <bits/stdc++.h>
using namespace std;
#define endl '\n'
mt19937 rng32(chrono::steady_clock::now().time_since_epoch().count());
mt19937_64 rng64(chrono::steady_clock::now().time_since_epoch().count());
int main(int argc, char* argv[]) {
ios_base::sync_with_stdio(0); cin.tie(NULL);
int n; cin >> n;
vector<int> cntx(101, 0);
vector<int> cnty(101, 0);
while (n--) {
int x, y;
cin >> x >> y;
cntx[x]++; cnty[y]++;
}
int distinctx = 0, distincty = 0;
for (int i=0; i<101; i++) {
distinctx += (cntx[i] > 0);
distincty += (cnty[i] > 0);
}
cout << min(distinctx, distincty) << endl;
return 0;
}
390B - Inna, Dima and Song
From the constraints given, for the i-th song, provided there exists corresponding xi and yi values, then the following inequality must hold: 2 ≤ xi + yi ≤ 2·ai.
Thus, if any bi is either lower than 2 or higher than 2·ai, then no xi and yi can be found, thus, Sereja's joy will surely decrease by 1.
Amongst all pairs of 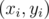 that xi + yi = bi, the pair with the highest value of xi·yi will be one with the equal value of xi = yi (this can be proven by the famous AM-GM inequality).
that xi + yi = bi, the pair with the highest value of xi·yi will be one with the equal value of xi = yi (this can be proven by the famous AM-GM inequality).
Thus, if bi is divisible by 2, we can easily pick  .
.
Also, from this, we can see (either intuitively or with static proofs) that the lower the difference between xi and yi is, the higher the value xi·yi will be. Thus, in case bi being odd, the most optimal pair will be 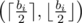 or
or 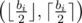 (the order doesn't matter here).
(the order doesn't matter here).
Time complexity: 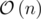 .
.
Submission link: 1010182
...
390C - Inna and Candy Boxes
...
Submission link: 1010182
...
390D - Inna and Sweet Matrix
...
Submission link: 1010182
...
390E - Inna and Large Sweet Matrix
...
Submission link: 1010182
...






