Since its data has been lost during the dark days of Codeforces, no version of it has been re-released, and I feel the round itself is quite educational, so I decided to give a try.
390A - Инна и будильники
The criterion shows that we can only use either vertical segments or horizontal segments.
Since there is no limit on the segments' length, we can see that it's always optimal to use a segment with infinite length (or may be known as a line).
We can see that the vertical line x = a will span through every alarm clocks standing at positions with x-coordinate being equal to a. In a similar manner, the horizontal line y = b will span through every alarm clocks standing at positions with y-coordinate being equal to b.
So, if we use vertical lines, the number of segments used will be the number of distinct values of x-coordinates found in the data. Similarly, the number of horizontal segments used will be the number of distinct values of y-coordinates found.
The process can be implemented by a counting array, or a map.
Time complexity: 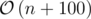 for regular arrays, or
for regular arrays, or 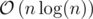 for maps.
for maps.
Submission link: 48211481
#pragma GCC optimize("Ofast")
#include <bits/stdc++.h>
using namespace std;
#define endl '\n'
mt19937 rng32(chrono::steady_clock::now().time_since_epoch().count());
mt19937_64 rng64(chrono::steady_clock::now().time_since_epoch().count());
int main(int argc, char* argv[]) {
ios_base::sync_with_stdio(0); cin.tie(NULL);
int n; cin >> n;
map<int, int> cntx, cnty;
while (n--) {
int x, y;
cin >> x >> y;
cntx[x]++; cnty[y]++;
}
cout << min(cntx.size(), cnty.size()) << endl;
return 0;
}
Submission link: 48211597
#pragma GCC optimize("Ofast")
#include <bits/stdc++.h>
using namespace std;
#define endl '\n'
mt19937 rng32(chrono::steady_clock::now().time_since_epoch().count());
mt19937_64 rng64(chrono::steady_clock::now().time_since_epoch().count());
int main(int argc, char* argv[]) {
ios_base::sync_with_stdio(0); cin.tie(NULL);
int n; cin >> n;
vector<int> cntx(101, 0);
vector<int> cnty(101, 0);
while (n--) {
int x, y;
cin >> x >> y;
cntx[x]++; cnty[y]++;
}
int distinctx = 0, distincty = 0;
for (int i=0; i<101; i++) {
distinctx += (cntx[i] > 0);
distincty += (cnty[i] > 0);
}
cout << min(distinctx, distincty) << endl;
return 0;
}
390B - Инна, Дима и песня
From the constraints given, for the i-th song, provided there exists corresponding xi and yi values, then the following inequality must hold: 2 ≤ xi + yi ≤ 2·ai.
Thus, if any bi is either lower than 2 or higher than 2·ai, then no xi and yi can be found, thus, Sereja's joy will surely decrease by 1.
Amongst all pairs of 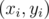 that xi + yi = bi, the pair with the highest value of xi·yi will be one with the equal value of xi = yi (this can be proven by the famous AM-GM inequality).
that xi + yi = bi, the pair with the highest value of xi·yi will be one with the equal value of xi = yi (this can be proven by the famous AM-GM inequality).
Thus, if bi is divisible by 2, we can easily pick  .
.
Also, from this, we can see (either intuitively or with static proofs) that the lower the difference between xi and yi is, the higher the value xi·yi will be. Thus, in case bi being odd, the most optimal pair will be 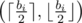 or
or 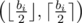 (the order doesn't matter here).
(the order doesn't matter here).
Time complexity: 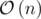 .
.
Submission link: 48212208
#pragma GCC optimize("Ofast")
#include <bits/stdc++.h>
using namespace std;
#define endl '\n'
mt19937 rng32(chrono::steady_clock::now().time_since_epoch().count());
mt19937_64 rng64(chrono::steady_clock::now().time_since_epoch().count());
int main(int argc, char* argv[]) {
ios_base::sync_with_stdio(0); cin.tie(NULL);
int n; cin >> n;
vector<int> a(n), b(n);
for (auto &z: a) cin >> z;
for (auto &z: b) cin >> z;
long long Joy = 0;
for (int i=0; i<n; i++) {
if (b[i] < 2 || b[i] > a[i] * 2) {Joy--; continue;}
int x = b[i] / 2, y = b[i] - x;
Joy += 1LL * x * y;
}
cout << Joy << endl;
return 0;
}
390C - Инна и коробки с конфетами
The query content looks pretty confusing at first, to be honest.
Since k is static throughout a scenario, we can group the boxes into k groups, the z-th box (in this editorial let's assume that the indices of the boxes start from 0) falls into group number 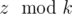 .
.
Then, each query can be simplified as this: "Is that true that among the boxes with numbers from li to ri, inclusive, the candies lie only in boxes of group 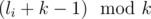 ?
?
To make sure the answer for a query being "Yes", Dima has to remove candies from all candied-box in all groups other than 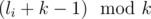 , while in that exact group, fill every empty box with a candy. Obviously, we'll consider boxes with indices between li and ri inclusively only.
, while in that exact group, fill every empty box with a candy. Obviously, we'll consider boxes with indices between li and ri inclusively only.
We can make k lists, the t-th (0-indexed) list stores the indices of candied boxes in group t.
We'll process with each query as the following:
- Obviously, given from the criteria, each range will consist of exactly
 boxes per each group. Let's denote
boxes per each group. Let's denote 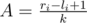 .
. - Traverse all groups, for the t-th group (again, 0-indexed), let's denote xt as the number of candied boxes of group t in the given range. This value can be calculated quickly through binary searching the constructed lists above.
- If group t is not the group being demanded to have candies (group
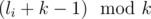 ), we'll need to perform xt actions (removing candies). Otherwise, we'll need to perform A - xt actions (adding candies to empty boxes).
), we'll need to perform xt actions (removing candies). Otherwise, we'll need to perform A - xt actions (adding candies to empty boxes).
Time complexity:  .
.
Submission link: 48212838
#pragma GCC optimize("Ofast")
#include <bits/stdc++.h>
using namespace std;
#define endl '\n'
mt19937 rng32(chrono::steady_clock::now().time_since_epoch().count());
mt19937_64 rng64(chrono::steady_clock::now().time_since_epoch().count());
int main(int argc, char* argv[]) {
ios_base::sync_with_stdio(0); cin.tie(NULL);
int n, k, w; string s;
cin >> n >> k >> w >> s;
vector< vector<int> > CandyModulo(k);
for (int i=0; i<n; i++) {
if (s[i] == '0') continue;
CandyModulo[i % k].push_back(i);
}
while (w--) {
int l, r;
cin >> l >> r; l--; r--;
int res = 0;
int demandedGroup = (l + k - 1) % k;
int BoxesPerGroup = (r - l + 1) / k;
for (int id=0; id<k; id++) {
int x = lower_bound(CandyModulo[id].begin(), CandyModulo[id].end(), l) - CandyModulo[id].begin();
int y = upper_bound(CandyModulo[id].begin(), CandyModulo[id].end(), r) - CandyModulo[id].begin();
if (id == demandedGroup) {
res += (BoxesPerGroup - (y - x));
}
else res += (y - x);
}
cout << res << endl;
}
return 0;
}
390D - Инна и матрица конфет
...
Submission link: 1010182
...
390E - Инна и большая матрица конфет
...
Submission link: 1010182
...






