Idea: ouuan
Consider the two edge cases: all the $$$z$$$ persons upvote / all the $$$z$$$ persons downvote. If the results are the same in these two cases, it is the answer. Otherwise, the result is uncertain.
#include <iostream>
using namespace std;
const char result[4] = {'+', '-', '0', '?'};
int solve(int x, int y)
{
return x == y ? 2 : x < y;
}
int main()
{
int x, y, z;
cin >> x >> y >> z;
cout << result[solve(x + z, y) == solve(x, y + z) ? solve(x, y) : 3];
return 0;
}
Idea: furry
- $$$m\ge\left\lfloor\frac n 2\right\rfloor+1$$$
Consider the chess pieces $$$1$$$ and $$$n$$$.
$$$\because\begin{cases}|r_1-r_n|+|c_1-c_n|\ge n-1\|r_1-r_n|\le m-1\|c_1-c_n|\le m-1\end{cases}$$$
$$$\therefore m-1+m-1\ge n-1$$$
$$$\therefore m\ge\frac{n+1}2$$$
$$$\because m\text{ is an integer}$$$
$$$\therefore m\ge\left\lfloor\frac n 2\right\rfloor+1$$$
- $$$m$$$ can be $$$\left\lfloor\frac n 2\right\rfloor+1$$$
If we put the $$$i$$$-th piece on $$$(r_i,c_i)$$$ satisfying $$$r_i+c_i=i+1$$$, it is a feasible plan, because $$$|r_i-r_j|+|c_i-c_j|\ge|r_i+c_i-r_j-c_j|$$$.
#include <cstdio>
using namespace std;
int main()
{
int n, i, ans;
scanf("%d", &n);
ans = n / 2 + 1;
printf("%d", ans);
for (i = 1; i <= ans; ++i) printf("\n%d 1", i);
for (i = 2; i <= n - ans + 1; ++i) printf("\n%d %d", ans, i);
return 0;
}
Idea: QAQAutoMaton
First, try to finish it without playing any empty cards.
If that's not possible, the best choice is to play several empty cards in a row, then play from $$$1$$$ to $$$n$$$. For a card $$$i$$$, suppose that it is in the $$$p_i$$$-th position in the pile ($$$p_i=0$$$ if it is in the hand), you have to play at least $$$p_i - i + 1$$$ empty cards. So the answer will be $$$\max\{p_i-i+1+n\}$$$.
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 200010;
int n, a[N], b[N], p[N], ans;
int main()
{
int i, j;
scanf("%d", &n);
for (i = 1; i <= n; ++i)
{
scanf("%d", a + i);
p[a[i]] = 0;
}
for (i = 1; i <= n; ++i)
{
scanf("%d", b + i);
p[b[i]] = i;
}
if (p[1])
{
for (i = 2; p[i] == p[1] + i - 1; ++i);
if (p[i - 1] == n)
{
for (j = i; j <= n && p[j] <= j - i; ++j);
if (j > n)
{
printf("%d", n - i + 1);
return 0;
}
}
}
for (i = 1; i <= n; ++i) ans = max(ans, p[i] - i + 1 + n);
printf("%d", ans);
return 0;
}
Idea: furry
First, if we choose a node as the root, then each subtree must be in a continuous arc on the circle. Then, we can use DP to solve this problem.
Let $$$f_u$$$ be the number of plans to draw the subtree of $$$u$$$, then $$$f_u=(|son(u)|+[u\ne root])!\prod\limits_{v\in son(u)}f_v$$$ — choose a position for each subtree and then $$$u$$$ itself, then draw the subtrees. However, instead of choosing the position of the root, we suppose the root is on a certain point on the circle, then rotate the circle, thus get the answer: $$$nf_{root}$$$.
In fact, we don't have to write a DP, the answer is $$$n$$$ times the product of the factorial of each node's degree ($$$n\prod\limits_{i = 1}^ndegree[i]$$$).
#include <iostream>
#include <cstdio>
using namespace std;
typedef long long ll;
const int N = 200010;
const int mod = 998244353;
int n, ans, d[N];
int main()
{
int i, u, v;
scanf("%d", &n);
ans = n;
for (i = 1; i < n; ++i)
{
scanf("%d%d", &u, &v);
ans = (ll) ans * (++d[u]) % mod * (++d[v]) % mod;
}
cout << ans;
return 0;
}
1172C1 - Nauuo and Pictures (easy version) and 1172C2 - Nauuo and Pictures (hard version)
Idea: ouuan
First, let's focus on a single picture with weight $$$w$$$ which Nauuo likes, so we only have to know the sum of the weights of the pictures Nauuo likes ($$$SA=\sum\limits_{i=1}^nw_i[a_i=1]$$$) and the sum of the disliked ones ($$$SB=\sum\limits_{i=1}^nw_i[a_i=0]$$$) instead of all the $$$n$$$ weights.
Then, we can use DP to solve this problem.
Let $$$f_w[i][j][k]$$$ be the expected weight of a picture Nauuo likes with weight $$$w$$$ after $$$i$$$ visits when $$$SA=j$$$ and $$$SB=k$$$ now.
Obviously, $$$f_w[0][j][k]=w$$$.
The state transition:
The next visit displays the picture we focus on. Probaility: $$$\frac w{j+k}$$$. Lead to: $$$f_{w+1}[i-1][j+1][k]$$$.
The next visit displays a picture Nauuo likes but is not the one we focus on. Probaility: $$$\frac{j-w}{j+k}$$$. Lead to: $$$f_w[i-1][j+1][k]$$$.
The next visit displays a picture Nauuo doesn't like. Probaility: $$$\frac k{j+k}$$$. Lead to: $$$f_w[i-1][j][k-1]$$$.
So, $$$f_w[i][j][k]=\frac w{j+k}f_{w+1}[i-1][j+1][k]+\frac{j-w}{j+k}f_w[i-1][j+1][k]+\frac k{j+k}f_w[i-1][j][k-1]$$$.
Let $$$g_w[i][j][k]$$$ be the expected weight of a picture Nauuo \textbf{doesn't like} with weight $$$w$$$ after $$$i$$$ visits when $$$SA=j$$$ and $$$SB=k$$$ now. The state transition is similar.
Note that $$$i,\,j,\,k,\,m$$$ have some relation. In fact we can let $$$f'_w[i][j]$$$ be $$$f_w[m-i-j][SA+i][SB-j]$$$ ($$$SA$$$ and $$$SB$$$ are the initial ones here).
But up to now, we can only solve the easy version.
To solve the hard version, let's introduce a lemma:
Proof:
Obviously, this is true when $$$i=0$$$.
Then, suppose we have already proved $$$f_w[i-1][j][k]=wf_1[i-1][j][k]$$$.
$$$\begin{aligned}f_1[i][j][k]&=\frac 1{j+k}f_2[i-1][j+1][k]+\frac{j-1}{j+k}f_1[i-1][j+1][k]+\frac k{j+k}f_1[i-1][j][k-1]\\&=\frac2{j+k}f_1[i-1][j+1][k]+\frac{j-1}{j+k}f_1[i-1][j+1][k]+\frac k{j+k}f_1[i-1][j][k-1]\\&=\frac{j+1}{j+k}f_1[i-1][j+1][k]+\frac k{j+k}f_1[i-1][j][k-1]\end{aligned}$$$
$$$\begin{aligned}f_w[i][j][k]&=\frac w{j+k}f_{w+1}[i-1][j+1][k]+\frac{j-w}{j+k}f_w[i-1][j+1][k]+\frac k{j+k}f_w[i-1][j][k-1]\\&=\frac{w(w+1)}{j+k}f_1[i-1][j+1][k]+\frac{w(j-w)}{j+k}f_1[i-1][j+1][k]+\frac {wk}{j+k}f_1[i-1][j][k-1]\\&=\frac{w(j+1)}{j+k}f_1[i-1][j+1][k]+\frac {wk}{j+k}f_1[i-1][j][k-1]\\&=wf_1[i][j][k]\end{aligned}$$$
Also, a brief but not so strict proof: the increment in each step is proportional to the expectation.
So, we only have to calculate $$$f_1[i][j][k]$$$ ($$$f'_1[i][j]$$$).
In conclusion:
$$$f'_1[i][j]=1\ (i+j=m)$$$
$$$f'_1[i][j]=\frac{SA+i+1}{SA+SB+i-j}f'_1[i+1][j]+\frac{SB-j}{SA+SB+i-j}f'_1[i][j+1]\ (i+j<m)$$$
$$$g'_1[i][j]=1\ (i+j=m)$$$
$$$g'_1[i][j]=\frac{SA+i}{SA+SB+i-j}g'_1[i+1][j]+\frac{SB-j-1}{SA+SB+i-j}g'_1[i][j+1]\ (i+j<m)$$$
If $$$a_i=1$$$, the expected weight of the $$$i$$$-th picture is $$$w_if'_1[0][0]$$$, otherwise, the expected weight is $$$w_ig'_1[0][0]$$$.
Last question: how to calculate the result modulo $$$998244353$$$?
If you don't know how, please read the wiki to learn it.
You can calculate and store all the $$$\mathcal O(m)$$$ inverses at first, then you can get an $$$\mathcal O(n+m^2+m\log p)$$$ solution instead of $$$\mathcal O(n+m^2\log p)$$$ ($$$p=998244353$$$ here).
#include <cstdio>
#include <algorithm>
using namespace std;
typedef long long ll;
const int N = 100010;
const int M = 3010;
const int mod = 998244353;
int qpow(int x, int y) //calculate the modular multiplicative inverse
{
int out = 1;
while (y)
{
if (y & 1) out = (ll) out * x % mod;
x = (ll) x * x % mod;
y >>= 1;
}
return out;
}
int n, m, a[N], w[N], f[M][M], g[M][M], inv[M << 1], sum[3];
int main()
{
int i,j;
scanf("%d%d", &n, &m);
for (i = 1; i <= n; ++i) scanf("%d", a + i);
for (i = 1; i <= n; ++i)
{
scanf("%d", w + i);
sum[a[i]] += w[i];
sum[2] += w[i];
}
for (i = max(0, m - sum[0]); i <= 2 * m; ++i) inv[i] = qpow(sum[2] + i - m, mod - 2);
for (i = m; i >= 0; --i)
{
f[i][m - i] = g[i][m - i] = 1;
for (j = min(m - i - 1, sum[0]); j >= 0; --j)
{
f[i][j] = ((ll) (sum[1] + i + 1) * f[i + 1][j] + (ll) (sum[0] - j) * f[i][j + 1]) % mod * inv[i - j + m] % mod;
g[i][j] = ((ll) (sum[1] + i) * g[i + 1][j] + (ll) (sum[0] - j - 1) * g[i][j + 1]) % mod * inv[i - j + m] % mod;
}
}
for (i = 1; i <= n; ++i) printf("%d\n", int((ll) w[i] * (a[i] ? f[0][0] : g[0][0]) % mod));
return 0;
}
Idea: furry
Consider this problem:
the person in $$$(i,1)$$$ facing right is numbered $$$a_i$$$, the person in $$$(1,i)$$$ facing bottom is numbered $$$b_i$$$. The person numbered $$$p_i$$$ has to exit the grid from $$$(i,n)$$$, the person numbered $$$q_i$$$ has to exit the grid from $$$(n,i)$$$.
The original problem can be easily transferred to this problem. And now let's transfer it into an $$$(n-1)\times (n-1)$$$ subproblem by satisfying the requirement of the first row and the first column.
If $$$a_1=p_1$$$ and $$$b_1=q_1$$$, you can simply do nothing and get an $$$(n-1)\times (n-1)$$$ subproblem.
Otherwise, you can set a portal consisting of two doors in $$$(x,1)$$$ and $$$(1,y)$$$ where $$$a_x=p_1$$$ and $$$b_y=q_1$$$. Swap $$$a_1$$$ and $$$a_x$$$, $$$b_1$$$ and $$$b_y$$$, then you will get an $$$(n-1)\times(n-1)$$$ subproblem.
Then, you can solve the problem until it changes into a $$$1\times1$$$ one.
This problem can be solved in $$$\mathcal O(n)$$$, but the checker needs $$$\mathcal O(n^2)$$$.
#include <iostream>
#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;
const int N = 1010;
struct Portal
{
int x, y, p, q;
Portal(int _x, int _y, int _p, int _q): x(_x), y(_y), p(_p), q(_q) {}
};
vector<Portal> ans;
int n, a[N], b[N], c[N], d[N], ra[N], rb[N], rc[N], rd[N];
int main()
{
int i;
scanf("%d", &n);
for (i = 1; i <= n; ++i)
{
scanf("%d", a + i);
ra[a[i]] = i;
}
for (i = 1; i <= n; ++i)
{
scanf("%d", b + i);
rb[b[i]] = i;
}
for (i = 1; i <= n; ++i) c[i] = d[i] = rc[i] = rd[i] = i;
for (i = 1; i < n; ++i)
{
if (c[i] == ra[i] && d[i] == rb[i]) continue;
ans.push_back(Portal(i, rc[ra[i]], rd[rb[i]], i));
int t1 = c[i];
int t2 = d[i];
swap(c[i], c[rc[ra[i]]]);
swap(d[i], d[rd[rb[i]]]);
swap(rc[ra[i]], rc[t1]);
swap(rd[rb[i]], rd[t2]);
}
printf("%d\n", ans.size());
for (auto k : ans) printf("%d %d %d %d\n", k.x, k.y, k.p, k.q);
return 0;
}
Idea: ODT
For each color, we can try to maintain the number of simple paths that do not contain such color.
If we can maintain such information, we can easily calculate the number of simple paths that contain a certain color, thus get the answer.
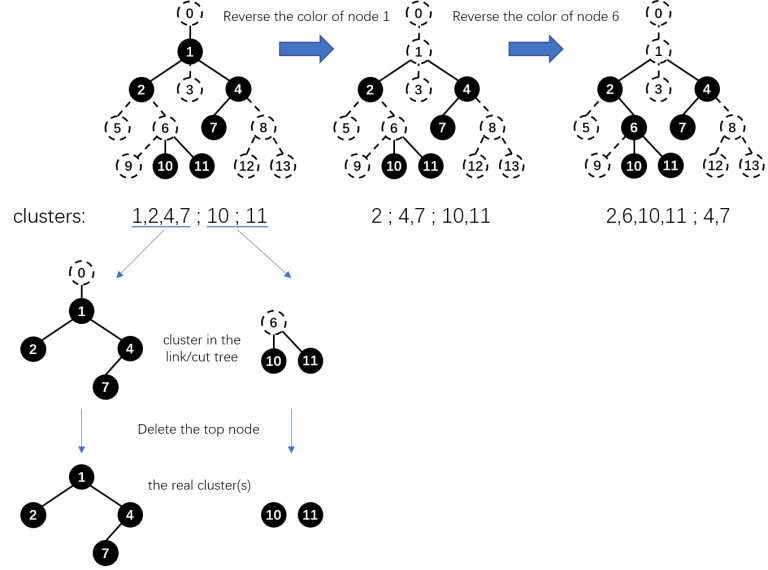
For each color, we delete all nodes that belong to such color, thus splitting the tree into some clusters (here we define a "cluster" as a connected subgraph of the original tree).
By maintaining $$$\sum\text{cluster size}^2$$$, we can get the number of simple paths that do not contain such color.
For each color we try to maintain the same information, add them together, and get the answer.
So now the problem is: a white tree
reverse the color of a node ( white <-> black )
output $$$\sum\text{cluster size}^2$$$
This problem can be solved by many data structures like top tree, link/cut tree or heavy path decomposition.
Let's use the link/cut tree for example.
You can maintain the size of each subtree and the sum of $$$\text{size}^2$$$ of each node's sons. Link/cut one node with its father (choose a node as the root and make the tree a rooted-tree first) when its color changes. In this way, the real clusters are the ones that are still connected after deleting the top node of a cluster in the link/cut tree. Update $$$\sum\text{cluster size}^2$$$ while linking/cutting.
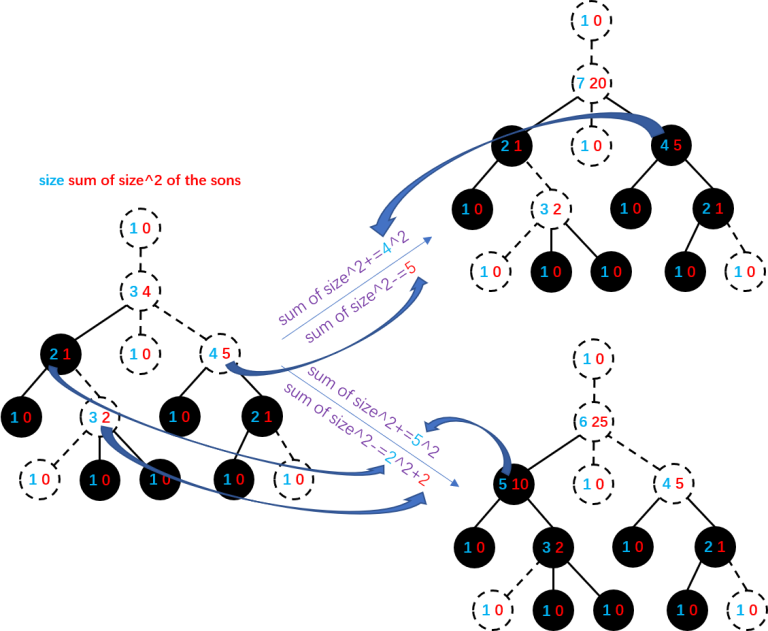
link:
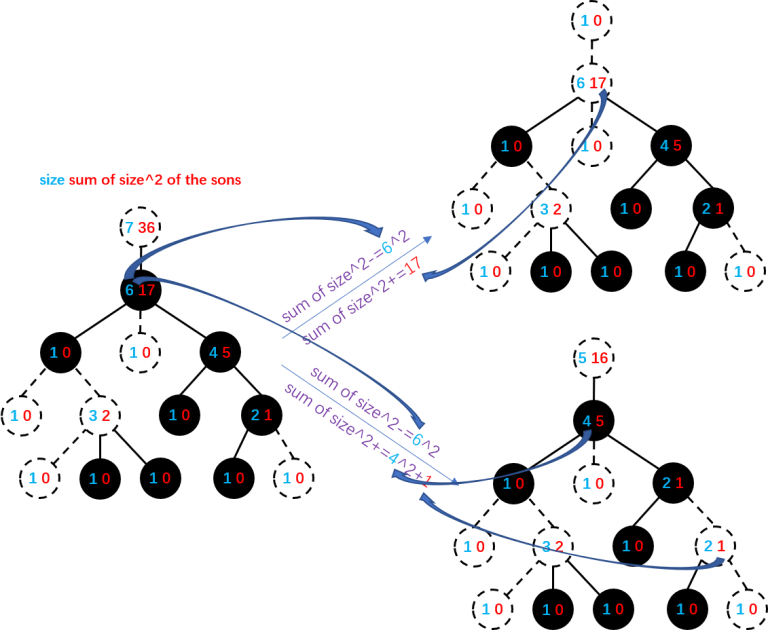
cut:
#include <algorithm>
#include <cctype>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <vector>
using namespace std;
typedef long long ll;
const int N = 400010;
struct Node
{
int fa, ch[2], siz, sizi;
ll siz2i;
ll siz2() { return (ll) siz * siz; }
} t[N];
bool nroot(int x);
void rotate(int x);
void Splay(int x);
void access(int x);
int findroot(int x);
void link(int x);
void cut(int x);
void pushup(int x);
void add(int u, int v);
void dfs(int u);
int head[N], nxt[N << 1], to[N << 1], cnt;
int n, m, c[N], f[N];
ll ans, delta[N];
bool bw[N];
vector<int> mod[N][2];
int main()
{
int i, j, u, v;
ll last;
scanf("%d%d", &n, &m);
for (i = 1; i <= n; ++i)
{
scanf("%d", c + i);
mod[c[i]][0].push_back(i);
mod[c[i]][1].push_back(0);
}
for (i = 1; i <= n + 1; ++i) t[i].siz = 1;
for (i = 1; i < n; ++i)
{
scanf("%d%d", &u, &v);
add(u, v);
add(v, u);
}
for (i = 1; i <= m; ++i)
{
scanf("%d%d", &u, &v);
mod[c[u]][0].push_back(u);
mod[c[u]][1].push_back(i);
c[u] = v;
mod[v][0].push_back(u);
mod[v][1].push_back(i);
}
f[1] = n + 1;
dfs(1);
for (i = 1; i <= n; ++i) link(i);
for (i = 1; i <= n; ++i)
{
if (!mod[i][0].size())
{
delta[0] += (ll)n * n;
continue;
}
if (mod[i][1][0])
{
delta[0] += (ll)n * n;
last = (ll)n * n;
} else
last = 0;
for (j = 0; j < mod[i][0].size(); ++j)
{
u = mod[i][0][j];
if (bw[u] ^= 1)
cut(u);
else
link(u);
if (j == mod[i][0].size() - 1 || mod[i][1][j + 1] != mod[i][1][j])
{
delta[mod[i][1][j]] += ans - last;
last = ans;
}
}
for (j = mod[i][0].size() - 1; ~j; --j)
{
u = mod[i][0][j];
if (bw[u] ^= 1)
cut(u);
else
link(u);
}
}
ans = (ll) n * n * n;
for (i = 0; i <= m; ++i)
{
ans -= delta[i];
printf("%I64d ", ans);
}
return 0;
}
bool nroot(int x) { return x == t[t[x].fa].ch[0] || x == t[t[x].fa].ch[1]; }
void rotate(int x)
{
int y = t[x].fa;
int z = t[y].fa;
int k = x == t[y].ch[1];
if (nroot(y)) t[z].ch[y == t[z].ch[1]] = x;
t[x].fa = z;
t[y].ch[k] = t[x].ch[k ^ 1];
t[t[x].ch[k ^ 1]].fa = y;
t[x].ch[k ^ 1] = y;
t[y].fa = x;
pushup(y);
pushup(x);
}
void Splay(int x)
{
while (nroot(x))
{
int y = t[x].fa;
int z = t[y].fa;
if (nroot(y)) (x == t[y].ch[1]) ^ (y == t[z].ch[1]) ? rotate(x) : rotate(y);
rotate(x);
}
}
void access(int x)
{
for (int y = 0; x; x = t[y = x].fa)
{
Splay(x);
t[x].sizi += t[t[x].ch[1]].siz;
t[x].sizi -= t[y].siz;
t[x].siz2i += t[t[x].ch[1]].siz2();
t[x].siz2i -= t[y].siz2();
t[x].ch[1] = y;
pushup(x);
}
}
int findroot(int x)
{
access(x);
Splay(x);
while (t[x].ch[0]) x = t[x].ch[0];
Splay(x);
return x;
}
void link(int x)
{
int y = f[x];
Splay(x);
ans -= t[x].siz2i + t[t[x].ch[1]].siz2();
int z = findroot(y);
access(x);
Splay(z);
ans -= t[t[z].ch[1]].siz2();
t[x].fa = y;
Splay(y);
t[y].sizi += t[x].siz;
t[y].siz2i += t[x].siz2();
pushup(y);
access(x);
Splay(z);
ans += t[t[z].ch[1]].siz2();
}
void cut(int x)
{
int y = f[x];
access(x);
ans += t[x].siz2i;
int z = findroot(y);
access(x);
Splay(z);
ans -= t[t[z].ch[1]].siz2();
Splay(x);
t[x].ch[0] = t[t[x].ch[0]].fa = 0;
pushup(x);
Splay(z);
ans += t[t[z].ch[1]].siz2();
}
void pushup(int x)
{
t[x].siz = t[t[x].ch[0]].siz + t[t[x].ch[1]].siz + t[x].sizi + 1;
}
void add(int u, int v)
{
nxt[++cnt] = head[u];
head[u] = cnt;
to[cnt] = v;
}
void dfs(int u)
{
int i, v;
for (i = head[u]; i; i = nxt[i])
{
v = to[i];
if (v != f[u])
{
f[v] = u;
dfs(v);
}
}
}
Idea: rushcheyo
The tutorial will be ready soon. The basic idea is to maintain a piecewise function using the segment tree.
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1000005;
const ll inf = (ll)1e16;
int n, m, P, a[N];
ll sum[N];
vector<ll> func[N << 2];
vector<ll> merge(int l, int r, int mid, const vector<ll> &f, const vector<ll> &g) {
ll suml = sum[mid] - sum[l - 1], sumr = sum[r] - sum[mid];
vector<ll> ret(f.size() + g.size() - 1, inf);
for (int i = 0, j = 0; i < (int)f.size(); ++i) {
ll xl = f[i], xr = (i + 1 == (int)f.size() ? inf : f[i + 1] - 1), yl = xl + suml - (ll)i * P, yr = xr + suml - (ll)i * P;
while (j > 0 && g[j] > yl) --j;
while (j < (int)g.size() && (j == 0 || g[j] <= yl)) ++j;
--j;
for (; j < (int)g.size() && g[j] <= yr; ++j)
ret[i + j] = min(ret[i + j], max(xl, g[j] - suml + (ll)i * P));
}
ret[0] = -inf;
return ret;
}
void build(int u, int l, int r) {
if (l == r) {
func[u].push_back(-inf);
func[u].push_back(P - a[l]);
return;
}
int mid = l + r >> 1;
build(u << 1, l, mid);
build(u << 1 | 1, mid + 1, r);
func[u] = merge(l, r, mid, func[u << 1], func[u << 1 | 1]);
}
ll query(int u, int l, int r, int ql, int qr, ll now) {
if (l >= ql && r <= qr)
return now + sum[r] - sum[l - 1] - (ll)P * (upper_bound(func[u].begin(), func[u].end(), now) - func[u].begin() - 1);
int mid = l + r >> 1;
if (qr <= mid)
return query(u << 1, l, mid, ql, qr, now);
if (ql > mid)
return query(u << 1 | 1, mid + 1, r, ql, qr, now);
return query(u << 1 | 1, mid + 1, r, ql, qr, query(u << 1, l, mid, ql, qr, now));
}
int main() {
scanf("%d%d%d", &n, &m, &P);
for (int i = 1; i <= n; ++i)
scanf("%d", a + i), sum[i] = sum[i - 1] + a[i];
build(1, 1, n);
for (int l, r; m--;) {
scanf("%d%d", &l, &r);
printf("%I64d\n", query(1, 1, n, l, r, 0));
}
return 0;
}





