I think lots of resource in online about this topics. But i thought i can explain it with a better way.
When Centroid Decomposition comes?
- Suppose a problem says that how many paths have length exactly k in a tree.
- Or, how many paths have xor k.
- Sum of all xor path in a tree.
- update a node Black to white or white to black. now query the shortest path from a node to a white node. etc.
So , it is clear , when a paths problem comes then we can use Centroid Decomposition.
For single node query or from a specific node , Dsu on Tree may do it.
Algorithm:
1. Find a centroid of current tree T.
What is Centroid?
Simply Centroid is a node, if we delete it. It makes some subtrees where every subtree size must be less than sz/2 { sz is the size of current tree T.}
How can we find it?
=> Take a node random node of current tree T. Now if its every subtree size less than sz/2. Then it is a centroid. => If not, go to highest size of subtree.
Note : In a tree only two Centroid possible From Jordan Theorem
=> Same thing must be done.
In this graph. If we start from node 1. Then Size[2]=7 which is larger than 11/2. so 1 is not centroid. Go to the 2. Now every subtree size less than 11/2. So for this graph centroid is 2.
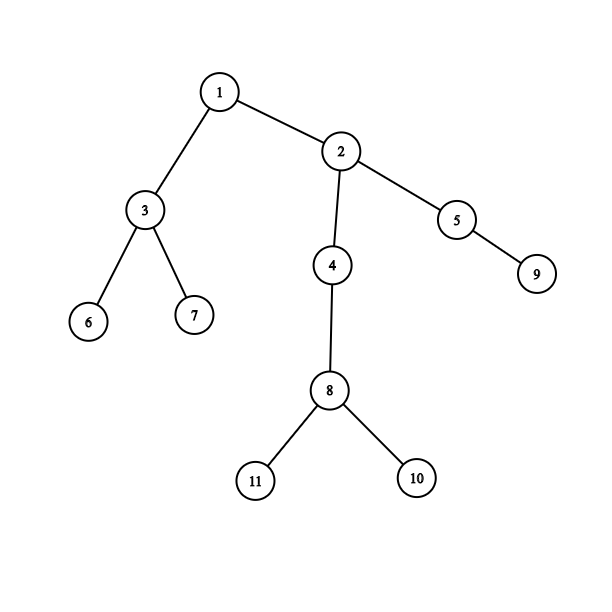
Here is the code for finding centroid of current Tree.
/// 'u' will give us the centroid
int u = _u;
while (true) {
int nu = -1;
for (int v : e[u]) {
if (!tocheck[v] || v == p[u]) continue;
if (1 + size[v] > sz / 2) nu = v;
}
if (sz — 1 — size[u] > sz / 2 && p[u] != -1
&&tocheck[p[u]]) nu = p[u];
if (nu != -1) u = nu; else break;
}
/// tocheck array check whether this node already done as a centroid of any tree or not
/// For size array you need just a dfs call
void dfs(int u) {
for (int v : e[u]) {
if (v == p[u]) continue;
p[v] = u;
dfs(v);
size[u] += 1 + size[v];
}
}
2. Problem Solving part.
Before Deleting centroid. we must find the answer for current Tree T.
**You must solve this part with O(sz) time**
suppose we need to find how many paths length equal k. Then we need to compute for current tree T.
**how many paths go through the centroid of T which length equal k?**
Take your time and think about it. If we call a dfs from centroid node and find the length of all node from centoid , then it will be easiar for us.
void dfs2(int u,int p,int val,bool flag)
{
if(flag) cnt[val]++;
else cnt[val]--;
for(auto v : e[u])
{
if(tocheck[v] && v!=p)
{
dfs2(v,u,val+1,flag);
}
}
}
void solve(int u,int p,int val)
{
if(val>k) return ;
sol+=cnt[k-val];
for(auto v : e[u])
{
if(tocheck[v] && v!=p)
{
solve(v,u,val+1);
}
}
}
void func(int u,int par)
{
sol=0;
dfs2(u,par,0,1);
sol+=cnt[k];
for(auto X : e[u])
{
if(tocheck[X])
{
dfs2(X,u,1,0);
solve(X,u,1);
dfs2(X,u,1,1);
}
}
ans+=sol/2;
}
3. Delete the Centroid node C and find the new centroid of all subtrees.
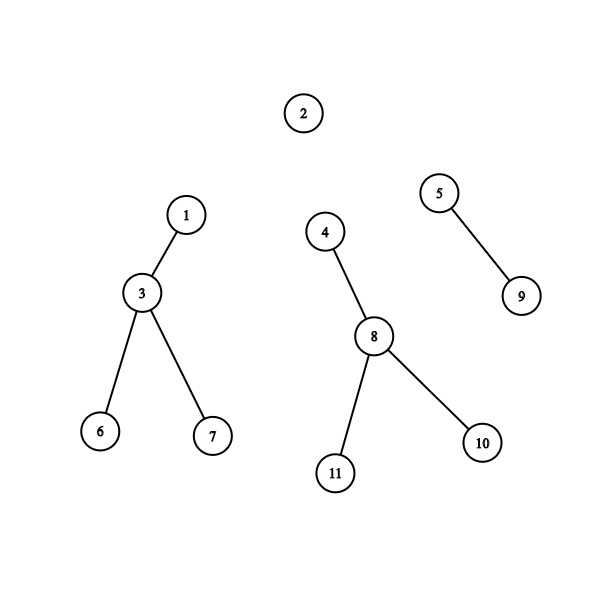
4. Repeat same Thing from 1 to 3 for every subtree.
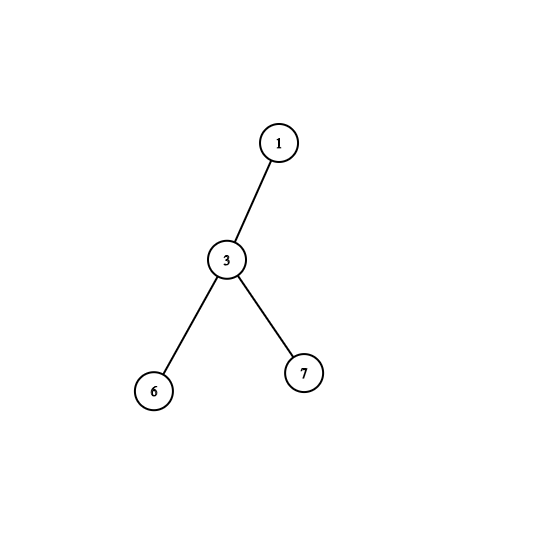
Property:
- The main property here is every node comes logn times under a centroid. So total complexity NlogN .
- Any path property like distance/xor/sum/etc. we can compute (logn+logn)times. Cause Highest depth for centroid Tree is logn.
- LCA of any two node in centroid tree logn.
Full Code is here for finding all path length equal to k
#define ll long long
#define vi vector<int >
#define vil vector<ll >
#define pb push_back
#define fi first
#define sc second
#define pii pair<int , int >
const int N = 500050;
const int INF = 1e9+100;
ll sol,k,ans;
struct CentroidDecomposition {
/// cd for Centroid Tree
/// e for Main tree
vector<vi> cd, &e;
/// tocheck for checking a node is already in centroid tree or not?
vector<bool> tocheck;
/// p for tracking parent of a node
/// cnt for counting length
vi size, p,cnt;
/// centroid Tree root
int root;
CentroidDecomposition(vector<vi> &tree) : e(tree) {
int sz = e.size();
tocheck.assign(sz, true);
col.assign(sz, false);
cd.assign(sz, vi());
p.assign(sz, -1);
cnt.assign(N, 0);
size.assign(sz, 0);
dfs(0);
root = decompose(0, sz,-1);
}
void dfs(int u) {
for (int v : e[u]) {
if (v == p[u]) continue;
p[v] = u;
dfs(v);
size[u] += 1 + size[v];
}
}
/// we can solve it for any amount of k
void dfs2(int u,int p,int val,bool flag)
{
if(flag) cnt[val]++;
else cnt[val]--;
for(auto v : e[u])
{
if(tocheck[v] && v!=p)
{
dfs2(v,u,val+1,flag);
}
}
}
void solve(int u,int p,int val)
{
if(val>k) return ;
sol+=cnt[k-val];
for(auto v : e[u])
{
if(tocheck[v] && v!=p)
{
solve(v,u,val+1);
}
}
}
/// finiding centroid and get answer for this centroid
int decompose(int _u, int sz,int par) {
int u = _u;
while (true) {
int nu = -1;
for (int v : e[u]) {
if (!tocheck[v] || v == p[u]) continue;
if (1 + size[v] > sz / 2) nu = v;
}
if (sz - 1 - size[u] > sz / 2 && p[u] != -1
&&tocheck[p[u]]) nu = p[u];
if (nu != -1) u = nu; else break;
}
for (int v = p[u]; v != -1 && tocheck[v]; v = p[v])
size[v] -= 1 + size[u];
sol=0;
dfs2(u,par,0,1);
sol+=cnt[k];
for(auto X : e[u])
{
if(tocheck[X])
{
dfs2(X,u,1,0);
solve(X,u,1);
dfs2(X,u,1,1);
}
}
ans+=sol/2;
dfs2(u,par,0,0);
tocheck[u] = false;
for (int v : e[u]) {
if (!tocheck[v]) continue;
int V2 = 1 + size[v];
if (v == p[u]) V2 = sz - 1 - size[u];
cd[u].push_back(decompose(v, V2,u));
}
return u;
}
};
int main(){
int n;
cin >> n>>k;
vector<vi> tree(n, vi());
for (int i = 0; i < n - 1; ++i) {
int a, b;
cin >> a >> b;
a--; b--;
tree[a].push_back(b);
tree[b].push_back(a);
}
CentroidDecomposition cd(tree);
cout<<ans<<endl;
return 0;
}
** More problem **
You can also check this for better understanding
Centroid Decomposition of a Tree by Tanuj Khattar
Sorry for bad grammatical issues. And this is my first tutorial blog, so don't take seriously formy mistakes
** Thank You **






