Problem: https://codeforces.net/contest/1373/problem/F
We will prove it is not possible if
- total capacities of the designed stations is smaller than total households of all cities. or
- for some continuous k stations, their total capacity is smaller than total households of (k-1) cities between them.
otherwise, it is always possible.
It is obvious that if condition 1 or 2 is meeted, it not possible. Now we prove it is the only senario that it is not possible.
Let us consider a circle segmented to n arcs with n nodes N1, N2, ... Nn. the length between Ni ans Ni+1 is ai(the number of households in the i-th city.) and there is a small ring in arc_i, note as Ci. the rings constrained by its node boundaries. For example ring C1 cannot move outside the bounds of N1 and N2. there is a rope with origin length bi between Ci and Ci+1. the rope can be stretched if necessary.
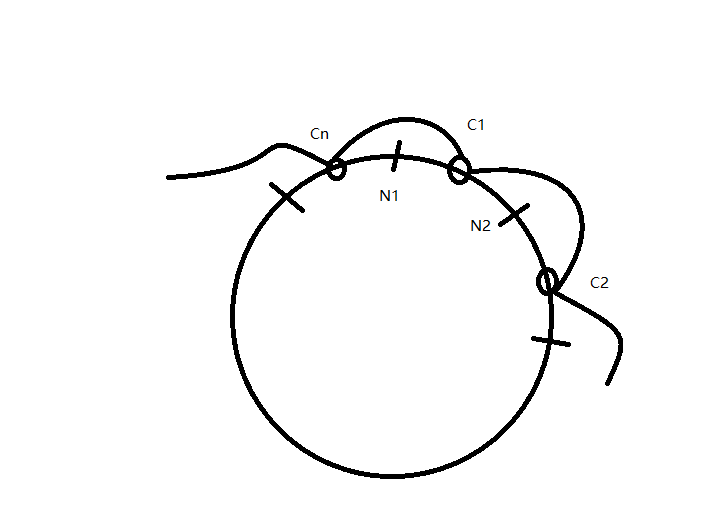
Now if we can arrange all the rings so that no rope need to be stretched, there is a solution.
We just let all rings move freely. if no rope are stretched, it is ok. If some ropes are streched. there are 2 conditions:
a. all ropes are streched, it is condition 1; b. some continuous ropes are streched, while the rope before and after them are not. In this case, the start and end ring of these ropes must be at the node. so it is condition 2.
end of proof. Sorry for my poor English.





