Disclaimer: I will not promise that this blog will make you code lca better. binary lifting is generally better than the following algorithms and i am only sharing it since i find it very interesting.

===================================================================================

intro (skip this if you know what lca is)

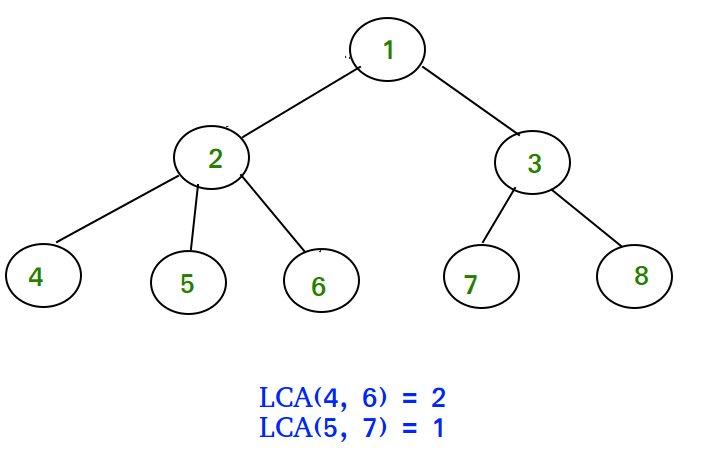
if you didnt know, lca stands for least common ancestor (and implies a rooted tree). so any ancestor of a nodeu. is any node on u's path to the root node (including the root itself). in the diagram below nodes 1 and 2 are both ancestors of node 4. so common ancestors of nodes u and v are the nodes that are both ancestors of u and ancestors of v. the least common ancestor of nodes u and v is first node that u and v share as an ancestor (first meaning the ancestor with the largest depth). and you can see in the picutre below the lca of 4 and 6 is 2, since that's the node with the furthest depth from the root that is both an ancestor of u and an ancestor of v. 1 does not count as the lca since 2 is further down and 5 does not count since it is not an ancestor of 4 (or 6 for that matter). for any pair of nodes on a rooted tree there is only one lca (hopefully this is intuitive), and this blog post describes ways to find that lca.

here is an image (from google search) of a tree. remember lca only works on a rooted tree since you have a sense of "up" and "down" only if there is a root

Sqrt LCA

imagine if we had a function k_up where k_up(u, k) returns the k'th node up from u. so from the diagram above k_up(2, 1) is 1 and k_up(8, 2) is also 1. this will be very helpful to do lca as we will see later. the array par[] stores for each u the direct parent of u (the parent of the root node is an imaginary node, 0 or -1 depending upon your implementation). in the diagram above par[2] = 1, par[5] = 2, and par[8] = 3.

so in all of the following code assume the par array is already calcutated, as for how to calculate it.... go google it.

int k_up(int u, int k){
   for(int i = 0; i<k; i++){
      u = par[u];
   }
   return u;
}

so what is the complexity of the above code? its O(k) since you loop over k to find par[u] k times. darn that's slow. i really wish we could do that faster. well that's the point of this blog.

so now lets pick a define a constant R, all we have to know abt R is that it's a constant <= the number of nodes on the tree. now for each u we define super[u] as the parent of u R times up (super for superparent, i love that word "superparent"). in the case that going k times from u takes us higher than the tree allows supor[u] = -1. so how does this help? so now in k_up(u, k) we can first loop over floor(k/R) times the superparent then we loop over k%R times on the parent array. so in total we move up floor(k/R)*R + k%R times (or k times :OOO). now the complexity is reduced to O(k/R + R) since the first half can only take k/R turns at most and the second half can take R steps at most. below is some code of the idea

const int R = 7777; //this is some random value since we dont define it yet
int k_up(int u, int k){
   while(k >= R) k = k/R, u = super[u];
   for(int i = 0; i<k; i++) u = par[u];
   return 0;
}

now there are a few problems, namely how ot find super[] and what is R, If we set R to be sqrt(n), O(k/R + R) is minimized. (hopefully the intuition makes sense), in fact picking R like this is so common its even got a name: "SQRT decomp". and to find super, you can for each u, loop up R times to find the parent R steps up. you can do this even faster, but im too lazy to cover that.

be sure you understand all of this since the conept of a k_up function will come up a lot later in this blog.

now onto the actual lca part. so consider a rooted tree and any two nodes u and v that are on the same level or have the same distance from the root. if we just marched from each node taking 1 step from each at the same time, the first node where they are the same is their lca. (note this only works if u and v start on the same level). so below is an implementation of the idea

int lca(int u, int v){ //remember that they have the same depth
  while(u != v){ 
    u = par[u], v = par[v];
  }
  return u;
}

so whats the complexity of this code? its O(d) where d is the difference of depth from the lca to node u (or v). this at worst case an be O(n) where n is the number of nodes in the tree (imagine a chain). so what can we do to speed it up? let us refer to the super array again. so if super[u] == super[v] then we know that the lca of u and v has to be super[u] or further down the tree. since if it was further up, we'd just take super[u] instead since super[u] is an ancestor of u and super[v] is an ancestor of v (and they are the same :O). so now (remember nodes u and v have the same depth) we can just loop over the super[u] and super[v] while they are different, and when they are the same, we'll loop over the parent array. below is the code for this idea.

int lca(int u, int v){ //remember that they have the same depth
  while(super[u] != super[v]){ 
    u = super[u], v = super[v];
  }
  while(u != v){
    u = par[u], v = par[v];
  }
  return u;
}