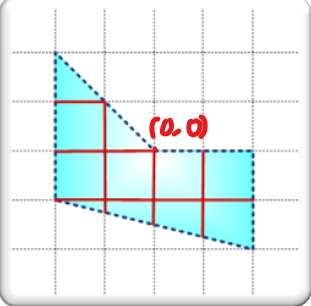
Given a polygon $$$n (n \leq 10 ^ 5) $$$ vertices on a 2D Descartes plane. $$$(|x_i|,|y_i| \leq 5. 10^8)$$$. This polygon is not self-intersecting, 2 consecutive edges have only 1 common point (which is the vertex). Find the sum of all segments of the 2D plane lie completely inside the polygon. (can be a real number).
Input:
5
0 0
-2 2
-2 -1
2 -2
2 0
Output: 12.5
Explain: The answer is the sum of all the red segments. The middle point is $$$(0,0)$$$.