| # | User | Rating |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 158 |
| 5 | atcoder_official | 157 |
| 6 | Qingyu | 156 |
| 7 | djm03178 | 151 |
| 7 | adamant | 151 |
| 9 | luogu_official | 150 |
| 10 | awoo | 147 |
UPD note that the score distribution has changed
UPD2: LHiC found a bug in the author solution of div1-F. We are working on the situation.
UPD3: we found a correct solution for div1-F and both submissions made during the contest pass all the tests against the correct solution. The round remains rated.
Hi, everybody,
Codeforces round 488 for both divisions will take place on Jun/16/2018 19:35 (Moscow time). The round will be 2.5 hours long (which is 30 minutes longer than usual).
The contest is created by NEAR and its friends. NEAR is working on teaching machines to compete in programming competitions. Read our blog post to learn more about the state of the art in the program synthesis today, our vision, and how you can help us bring this vision to reality.
The contest will feature 6 problems for each division, with 4 problems shared across them.
The problems for the contest are from the test rounds hosted on a system JavaBlitz last year. If you participated in any of the JavaBlitz rounds, you shall not participate in this round.
The score distribution in the first division is 500-1000-1000-1500-2250-3000
In the second -- 500-1000-1500-2000-2000-2500
The round is rated for both divisions.
All problems are initially created by myself, Alexander "AlexSkidanov" Skidanov, and by Nikita "FalseMirror" Bosov. David "pieguy" Stolp, Alexander "AlexFetisov" Fetisko, Marcelo "mnaeraxr" Fornet, Nikolay "KAN" Kalinin and Mikhail "cerealguy" Kever helped tremendously ensuring the high quality of the problems.
As a closing note, we are constantly looking for people to help us label competitive programming data for research. Read more here.
Congratulations to winners!
Div. 1:
Div. 2:
The editorial is published here. Thanks for your participation!
Hi,
Three days ago I wrote a big blog post about how we trying to teach machines to code (and in doing so bring the Singularity closer, since, you know, It's Near).
In this post I want to remind you that we pay people who help us annotate data from competitive programming archives, on average $12/hour.
If you are interested, the platform is here:
This is super convenient for people who practice for ICPC and can't have a full-time job.
Want to help in some other way? May be you know some competitive programming websites on which the solutions are public, like on CodeForces? Please share them with us.
Or may be you were actively solving problems on one of the sites with solutions kept private, and would not mind sharing your account with us? That would also help tremendously!
Let's bring the Singularity closer together!
Hi, all,
I with few other folks at NEAR work on teaching machines to program. A particularly exciting sub-project of that is teaching machines to solve competitive programming problems.
In this post I would like to give a quick overview of where the state of the art is today, what the major challenges are, why this is not a popular area of research, and how the CodeForces community can help to address some of the issues the program synthesis community is facing today.
We also have a certain budged allocated for this project, and we are paying to the CodeForces members who help us with some data annotation challenges. We have paid more than $10k in our first two annotation projects, and are launching three more projects today. Scroll to the end if you are interested.
Competitive programming as a benchmark
With the emergence of deep learning, neural networks started performing almost at a human level in many tasks: visual object recognition, translation between languages, speech recognition, and many other. One area where they haven't shown anything exciting yet is programming. I will talk about state of the art below, but overall neural networks are nowhere close today to doing actual coding.
But what would it even mean to solve programming? What would be a good benchmark and milestones to recognize? One such milestone is solving competitive programming. We are not talking here about building a bot that would perform at a tourist level, but at least solving A and B Division two would be super impressive. Even this is actually very hard for computers, and I will talk about why below in the Open Challenges section.
State of the art
The area of research that is tasked with automated program generation is called Program Synthesis. The two most common sub-areas of it are programming from examples (synthesizing a program from few input/output examples of what it should do) and programming from description (synthesizing a program from an English description).
Programming from examples has a long history. One known example that you can run in your browser is Magic Haskeller, which is a very sophisticated system that synthesizes rather nontrivial Haskell programs from just one example.
There were some applications of program synthesis from example in commercial products. Modern distributions of Excel come with a feature called FlashFill. If you have a column of names, and a column of last names, and enter an email in the third column in a form of "[email protected]", FlashFill will immediately synthesize a program that concatenates the first letter of the first name with a dot, the last name and the "@gmail.com" and suggest to auto-fill the rest of the column. This looks like magic, and took more than a year of work for a very strong team of program synthesis experts at Microsoft Research to deliver it.
Ultimately the lab that created FlashFill created a general purpose framework PROSE in which one can create services like FlashFill by describing a domain-specific language and writing few C# functions.
A separate epic paper from a different lab at MSR called TerpreT serves as a great review and comparison of different approaches to programming from examples. It compares using SMT solvers, linear programming and neural networks, and shows that as of today using more traditional approaches such as SMT solvers still noticeably outperforms deep learning approaches.
An early attempt to apply programming by example to solving competitive programming is a paper from the same lab called Deep Coder. It can synthesize short programs for very simple problems by seeing just a few examples, and uses a combination of both deep learning and several traditional approaches.

Another great inspiring example of applying program synthesis from examples is a paper called Chlorophyll, in which the technique is applied to optimizing assembly programs. It does it in the following way:
- Given a short program that needs to be optimized and a few tests (possibly zero), synthesize the shortest program that is consistent with the existing tests.
- Using an SMT solver, try to prove that the synthesized and the given programs produce the same output on all possible tests. If proven, the synthesized program is an optimized version of the given program. If disproved, the SMT solver would find a test on which the two programs produce different output. Add the test to the set of tests and go to (1).
Mindblowingly, not only this works, it generally converges for short programs in under 10 iterations!
Programming from description is a more recent area of research. Until the emergence of Deep Learning few years ago there was no sufficiently general way of extracting information from natural language. Arguably, even with the modern Deep Learning approaches natural language understanding is still at a pretty early stages, which is one of the major limitations.
There were papers that attempt to solve synthesis of SQL, BASH and Java from description, but they all face the challenges described below. To my best knowledge no application of synthesis from description appears in any commercial product today.
Who works on Program Synthesis?
Number of labs that work on program synthesis is actually rather small. Besides NEAR, here are several well-known ones:
MIT lab lad by Armando Solar-Lezama
ETH Zurich lab (notably Veselin Raychev and Martin Vechev), which ultimately incorporated into DeepCode.ai
Microsoft Research has a long history of working on program synthesis. Here are two good publication aggregates: one and two.
Open Challenges
When we talk about programming from description, there are several large challenges, all remaining mostly unsolved as of today.
1. Lack of data
This might sound crazy -- GitHub has so much code that even just crawling all of it is a non-trivial task, how could the data be lacking? But as a matter of fact, the data that is readily available, such as GitHub or StackOverflow, is not immediately usable because it is very noisy. Here are some datasets that we considered, and what challenges they come with:
Small commits that fix a simple bug, and the text of the associated issue. The person who fixes a bug has a lot of context about how the code operates. This context varies drastically between projects, and without it even an experienced human expert would not be able to predict the change in the code given the issue text.
Commit messages and the code. Besides commits also depending significantly on the context (i.e. a human expert often won't be able to predict the code in the commit given a well-formed commit message), this dataset also has a lot of noise. People often provide incorrect commit messages, squash multiple features and fixes into one commit describing only one feature, or generally writing something like "Fixing a bug we found yesterday".
Docstrings and function bodies. This one was very promising, but has two issues: a) docstring describes how a function shall be used, not how it is implemented, and predicting code from the usage pattern is a harder task than predicting code from a task description; and b) even in very good codebases quality docstrings are usually only provided for the public APIs, and the internal code is generally way less documented.
On the other hand, there's also competitive programming archives. Competitive programming as a dataset has several advantages:
The code is short and self-contained.
No context besides the problem statement is needed to write it.
The dataset of statements and accepted solutions is very clean -- accepted solutions almost certainly solve the problem from the statement.
There are however some challenges:
While the number of solutions is very high (CodeForces alone has dozens of millions), the number of different problems is somewhat low. Our estimate suggests that the total number of different competitive programming problems in existence is somewhere between 200k and 500k, with ~50k being attainable with solutions when a reasonable effort is made. Only 1/3 of those problems are easy problems, so we are looking at having ~17k problems available for training.
The statements contain a lot of fluff. Alice and Bob walking on a street and finding a palindrome laying around is something I had in my nightmares on multiple occasions. This unnecessary fluff paired with relatively low number of problem statements further complicates training the models.
The lack of data is also the primary reason why program synthesis is not a popular area of research, since researchers prefer to work on existing datasets rather than figuring out where to get data from. One anecdotal evidence is the fact that after MetaMind published the WikiSQL dataset, multiple papers were immediately submitted to the coming conferences, creating a minor spike in program synthesis popularity, despite the fact that the quality of the dataset is very low.
Having said that, annotating the competitive programming dataset to a usable state would increase the popularity of the field, bringing closer the moment when we are competing against bots, and not just humans.
2. External Knowledge
Consider the following problem that was recently given on CodeForces: given an array of numbers of size 5000, how many triplets of numbers are there in the array such that the XOR of the three numbers is zero, and the three numbers can be the sides of a non-degenerate triangle.
This is Div1 A/B level, with most people with experience solving it easily. However from a machine perspective it is extremely hard. Consider the following challenges:
The model would need to realize that it doesn't need to fix all three numbers, it is sufficient to fix two numbers, and check if their XOR exists in the array. (this is besides the fact that the model would need to understand that fixing three numbers would not fit into timelimit)
The model would need to somehow know what does it mean for three numbers to be sides of a non-degenerate triangle.
Out of 50k problems that we have collected, only few had used that particular property of XOR in a similar way, and only a few dozen were in some way referring to the property of the sides of the triangle. To make a machine learning model be able to solve such a problem, one of the three things will need to happen:
We will find a way to learn from few examples. One-shot learning is a hot topic of research, with some recent breakthroughs, but no existing approach would be immediately applicable here.
We will find a way to provide the model with some external knowledge. This is an area that hasn't been researched much, and even figuring out how that knowledge shall be represented is a challenging research task.
We will find a way to augment the dataset in such a way that a single concept that occurs only a few times in the dataset instead appears in a variety of contexts.
All three of those are open challenges. Until they are solved, we can consider an easier task: solving a competitive programming problem that is (either initially, or by the means of rewriting) very close to the solution, e.g:
"Given an array of numbers, are there two numbers a and b in that array such that c = a XOR b also appears in the array, and the largest number among a, b and c is smaller than the sum of the remaining two?"
Can we solve it? With the modern technology not yet, and it makes sense to learn how to solve such problems before we even get to the more complex one-shot learning part.
3. Inherent uncertainty in Deep Learning models
Deep Learning models by design are probabilistic. Each prediction they make has some certainty associated with it, and therefore they generally keep having some chance of making a mistake even when trained well. If a model predicts code one token at a time, and a code snipped comprises 200 tokens, the model with 99% per-token accuracy would mess up at least one token with probability 87%. In natural language translation this is acceptable, but in Program Synthesis messing up one token most likely leads to a completely wrong program.
Notably, more traditional approaches from code synthesis (used primarily for programming by examples) don't suffer from the same problem. Marrying classic programming languages approaches with deep learning approaches is very desirable, but at this time very little success was achieved.
Is it NEAR?
At NEAR, we are attempting to address many of the above problems. Here I will shortly cover our efforts that are relevant to solving competitive programming.
Data
As I mentioned above, even though competitive programming data is rather clean, it has some unnecessary fluff in the statements that we'd love to get rid of. For that we asked the community to rewrite problem statements in such a way that only a very formal and dry description of what exactly needs to be done is left.
We also used help of the community to collect a dataset of statement-solution pairs in which no external knowledge (such as properties of XOR or triangles) is needed to write the solution given the statement. We plan to release a large part of this dataset during NAMPI 2018, so stay tuned.
This dataset is a set of problems with statement super close to the solution. Such problems are easier for a machine than even the simplest real problems on a real contest, but this dataset not only serves as the first milestone (being able to solve it is a prerequisite to solving more complex problems), it is also a good curriculum learning step -- a model that was taught to solve such problems is expected to pick up solving more complex problems more easily than a model that was not.
Data augmentation
To augment the dataset above, we created an algorithm that gets a solution as an input, and produces a very low level statement (very close to the solution) as an output. The generator is built in such a way that the statements generated are close in terms of certain metrics to what people have written. Training on such generated dataset achieves a non-zero accuracy on the human generated dataset, and the closer we get the generated statements to what people write in terms of the measurable metrics (such as BLEU score), the better the accuracy of the trained model on the human-generated set is.
"Non-zero accuracy" might not sound very impressive, but if you consider the fact that it effectively means that the model manages to learn how to solve some (albeit very simple) human-generated problems by only being trained on a synthetic data, it is actually very promising, and is a huge step towards solving more complex problems, and ultimately solving actual contest problems on a live competition.
Fixing the uncertainty of Deep Learning models
At the core of our approaches are deep learning models that read in text and produce code as either a sequence of tokens, or an AST tree. Either way, as mentioned above, even a very well trained model has a very high chance of messing up at least one token.
Trying to address this problem is on its own very close to what competitive programmers do. We explore quite a few approaches. We presented one such approach in our ICLR workshop paper -- the idea is to perform a beam search on AST trees until we find an AST of a program that passes sample tests. By the time we were publishing that paper we didn't have a good human-annotated dataset yet, so all the results were presented on a semi-synthetic dataset, but the model itself was not changed much since then, and we still use it on the human-annotated data today.
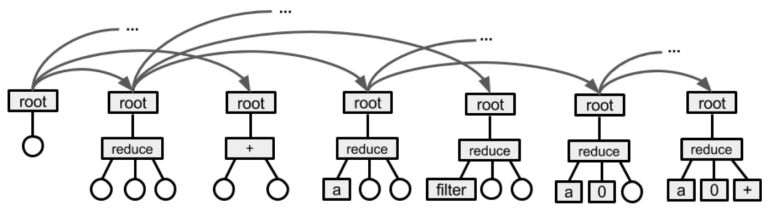
Running beam-search in the tree space is pretty slow and memory-consuming, and requires some tricky optimizations, such as using persistent trees, precomputing results on the go and others. Anyone knows a good place where I can find people who are good at writing complex algorithms on trees and who'd like to join a Silicon Valley-based VC-funded company that teaches machines to write code?
Another approach we researched is letting another (or the same) deep learning model to fix the program if the first program that was generated doesn't pass the samples. The high level idea is to train a model that takes as an input a problem statement and a program from the previous iteration alongside with some feedback on why the program is wrong, and generates a new program (either from scratch, or by producing a diff). We have a publication that reports some early results that was also accepted as a workshop paper at ICLR 2018.
To get to some more interesting ideas, let's consider us asking the model to implement a binary search. Imagine that it mistakenly swaps lines left = middle and right = middle. If you then feed the code back to the model, spotting this bug would be extremely hard. Even for humans it is a non-trivial task. So is the original source code the best medium to feed back to the model? One option we have been exploring is feeding an execution trace instead. If the model made the mistake above, the execution trace would always converge to one of the ends of the range instead of some value in the middle, which would provide way more information to the model than just the code itself. The challenge, however, is that execution traces of real programs are rather long, and condensing them to only show information that is likely to be relevant is an open and interesting challenge.
How can community help
If you find the concept interesting, and would like to help, there are (at least) two ways you can do it:
1. Help us annotate more data (and get paid for that!)
We run a labeling platform at
Where we ask people to help us rewrite statements or annotate solutions. We have paid out more than $10k in the last few months, and are launching three new tasks there today. The invitation code to register is NEAR.
You need to have sufficient written English skill to write statements that are understandable by English speakers to participate.
2. Help us get more solutions
If you were solving problems on informatics.mccme.ru, and would be willing to share your account with me to crawl it, that would provide a lot of value. The website has great intro level problems, and presently we have no solutions for them.
We also look for accounts on Timus, SPOJ, acmp.ru and main.edu.pl / szkopul.edu.pl.
Hi,
Wanted to remind the community that we host a project
Where we pay people for rewriting problem statements from online judges into short concise form. Most of the people who participate in the project today average between $10 and $12 per hour.
We use those rewritten statements to teach machines solve competitive programming problems.
We especially need people who can read Japanese or Romanian!
There's another way you can help tremendously with our effort. We need as many solutions from websites that do not make the submissions public. If you can share with us your account on Timus, SPOJ, e-olymp, acmp.ru, COJ, or any other website on which solutions can be seen after logging in, that would help a lot with our research (in case of COJ you can just download all your solutions on the website in one click and share the downloaded archive).
So far around 20 CodeForces users shared with us their accounts, thanks a lot to all of them!
Hi,
Myself together with a small team of researchers are trying to teach machines solve competitive programming problems.
For that we need a large dataset of problems and solutions.
We have already crawled practically all websites that have public solutions, and are now trying to crawl solutions that are not public.
If you were solving problems from Timus, UVa or any other platform with private submissions, and are open to giving us access to your account to crawl the solutions, please send your credentials to me via a personal message. It will help us a lot with our research. The language in which you were solving problems doesn't matter.
We won't publish your code anywhere, and won't use the credentials in any way except for crawling the solutions.
Besides that a reminder that we have a labeling platform where we are trying to rewrite competitive programming problem statements in a short concise way. We pay for doing it, and many people who are presently helping us are making $12/hour. The link to the platform is
It is a very nice way to get extra income for people who can't have a full-time job due to practicing for the upcoming competitions or studying.
Does anyone know someone from TOJ?
Trying to get in touch with them, but the email on the website is no longer valid.
UPDATE: the contest is over, the problems are available for upsolving. If you participated, please tell us how usable and responsive the interface was, and whether everything went well.
Hi, Everybody!
We would like to invite you all to help us test a new competitive programming platform called JavaBlitz.
JavaBlitz rounds are short (up to 2hr 30m) contests with ACM ICPC rules with the only difference that the penalty for an incorrect submission is 4 minutes instead of 20.
The platform only supports Java as the programming language, and, similar to TopCoder, requires participants to implement a method in the given class that receives the input as arguments and returns the result. There's no reading from- and writing to files.
The beta round will take place today, June 8th, at 20:30 Moscow Time / 17:30 UTC / 10:30 AM PDT.
The Beta Round will be 1hr 40min long and will feature three problems. No Div1 D/E level problems will be featured on this round.
The platform is located here: http://javablitz.com, and besides the coming Beta Round has two warmup problems to play around with the arena.
The probability of the system going down during the contest is very high, keep it in mind if you participate :)
Hi everyone,
Today we are going to show few demos of Sequence to Sequence models for code completion.
But before diving into details, we, as usual, want to ask you to participate in collecting data for the future models in our labeling platform here:
There are real money rewards associated with all the tasks in the platform.
The Demo
In the first demo we trained a seq2seq model, more on which below, on all the Accepted java solutions on CodeForces. The goal of the model is to predict the next token based on all the tokens seen so far. We then plug the output of the model into a code editor (the arena on the video is an unfinished project I will write about separately) to see how it behaves when one actually solves a competitive programming problem. Here we are solving problem A from Codeforces Round 407:
Notice how early on the model nearly perfectly predicts all the tokens, which is not surprising, since most of the Java solutions begin with rather standard imports, and the solution class definition. Later it perfectly predicts the entire line that reads n, but doesn’t do that well predicting reading k, which is not surprising, since it is a rather rare name for the second variable to be read.
There are several interesting moments in the video. First, note how after int n = it predicts sc, understanding that n will probably be read from the scanner (and while not shown in the video, if the scanner name was in, the model would have properly predicted in after int n =), however when the line starts with int ans =, it then properly predicts 0, since ans is rarely read from the input.
The second interesting moment is what happens when we are printing the answer. At first when the line contains System.out.println(ans it predicts a semicolon (mistakenly) and the closing parenthesis as possible next tokens, but not - 1, however when we introduce the second parenthesis System.out.println((ans, it then properly predicts -1, closing parenthesis, and the division by two.
You can also notice a noticeable pause before the for loop is written. This is due to the fact that using such artificial intelligence suggestions completely turns off the natural intelligence the operator of the machine possesses :)
One concern with such autocomplete is that in the majority of cases most of the tokens are faster to type than to select from the list. To address it, in the second demo we introduce beam search that searches for the most likely sequences of tokens. Here’s what it looks like:
Here there are more rough edges, but notice how early on the model can correctly predict entire lines of code.
Currently we do not condition the predictions on the task. Partially because number of tasks available on the Internet is too small for a machine learning model to predict anything reasonable (so, please help us fix it by participating here: https://r-nn.com). Once we have a working model that is conditioned on the statement, we expect it to be able to predict variable names, snippets to read and write data and computing some basic logic.
Let’s review Seq2Seq models in the next section.
Sequence to sequence models
Sequence to Sequence (Seq2Seq for short) has been a ground-breaking architecture in Deep Learning. Originally published by Sutskever, Vinyals and Le, this family of models achieved state-of-the-art results in Machine Translation, Parsing, Summarization, Text to Speech and other applications.
Generally Seq2Seq is an extension of regular Recurrent Neural Networks (we have mentioned them before in http://codeforces.net/blog/entry/52305), where model first encodes input tokens and then tries to produce set of output tokens by decoding on token at a time.
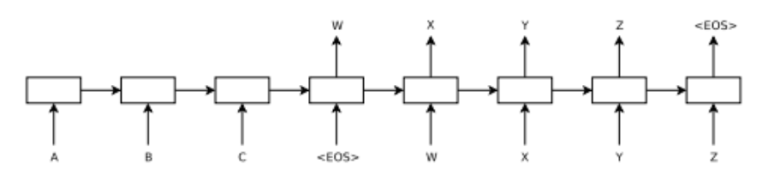
For example on this picture the model is first fed three inputs A, B and C and then it is given <EOS> token to indicate that it should start predicting output sequence [W, X, Y, Z]. Here each token is represented as a continuous vector [embedding] that is learned jointly with parameters of the RNN model.
At training time, model is fed with correct output tokens shifted by one, so it can learn dependencies in the data. The signal comes from maximizing the log probability of a correct output given the source sequence.
Once training is complete this model can be used to produce most probable output sequences. Usually to search for most likely decodings a simple left-to-right beam search is applied. Beam search is a greedy algorithm of keeping a small number B of partial hypotheses to find the most likely decoding. At each step we extend these hypotheses by every possible token in the vocabulary and then discard all but B most likely hypotheses according to model’s probability. As soon as “” (End of Sequence) symbol is appended to hypothesis, it is removed from the beam and is added to a set of complete hypotheses.
The model that we use right now is not a seq2seq per se, since there’s no input sequence given to it, so it only consists of the decoder part of the seq2seq. After being trained on the entire set of CodeForces java solutions, it achieved 68% accuracy of predicting the next token correctly, and 86% of predicting it among top 5 predictions. If the first character of the token is already known, the prediction reaches 94%. It is unlikely that a vanilla seq2seq will achieve a performance sufficient to be usable in practice, but it establishes a good baseline to compare the future models against.
Hi, everyone,
As I mentioned in the last post, myself and a friend of mine got very interested in how close we can get machines to writing software, and whether modern advances in Deep Learning can help us build tools that considerably improve the way people write, review and debug code.
I want to start a series of posts discussing some interesting advances in using machine learning for both writing and executing code.
This particular post is about a machine learning model proposed early last year by Scott Reed from University of Michigan, then an intern at Google DeepMind, called Neural Programmer-Interpreters.
But before I go into the details, I would like to start with an ask. CodeForces and similar websites today host a vast amount of data that we would love to use to train our machine learning models. A particular challenge is that problem statements historically contain a lot of unnecessary information in an attempt to entertain competitors. Machine Learning models do not get entertained, but rather get very confused. We want to rewrite all the statements of all the problems available on the Internet in a very concise manner, so that a machine learning model has a chance of making sense of them. Thanks to people who volunteered after the last post, we now have more or less tested our labeling platform, and would like to invite everybody to help us create that dataset.
The platform is located here:
There's a monetary reward associated with labeling the solutions. Based on my own performance, and performance of those people who helped us with testing, after some practice it takes on average 2 to 4 minutes to write one short statement, which ends up paying around $6/hour. Something reasonable to consider for those who practice for upcoming competitions and don't have time for a full time job. On top of that, participating in the project is a great way to contribute to pushing science forward.
Now, back to the actual topic of the article.
Neural Programmer-Interpreters
Neural programmer-interpreter, or NPI for short, is a machine learning model that learns to execute programs given their execution traces. This is different from some other models, such as Neural Turing Machines, that learn to execute programs only given example input-output pairs.
Internally NPI is a recurrent neural network. If you are unfamiliar with recurrent neural networks, I highly recommend reading this article by Andrej Karpathy, that shows some very impressive results of very simple recurrent neural networks: The Unreasonable Effectiveness of Recurrent Neural Networks.
The setting in which NPI operates consists of an environment in which a certain task needs to be executed, and some low level operations that can be performed in such environment. For example, a setting might comprise:
- An environment as a grid in which each cell can contain a digit; and a cursor in each row of the grid pointing to one of the cells;
- A task of adding up two multidigit numbers;
- Low-level operations including "move cursor in one of the rows" and "write a digit":

Given an environment and low-level operations, one can define high level operations, similar to how we define methods in our programs. A high level operation is a sequence of both low-level and high level operations, where the choice of each operation depends on the state of the environment. While internally such high level operations might have branches and loops, those are not known to the NPI. NPI is only given the execution traces of the program. For example, consider a maze environment, in which a robot is trying to find an exit, and uses low-level operations LOOK_FORWARD, TURN_LEFT, TURN_RIGHT and GO_STRAIGHT. A high level operation make_step can be of a form:
has_wall = LOOK_FORWARD
if (has_wall)
with 50% chance: TURN_RIGHT
else: TURN_LEFT
else: GO_STRAIGHTIf NPI was then to learn another high level operation that just continuously calls to make_step, the data that is fed to it would be some arbitrary rollout of the execution, such as
make_step
LOOK_FORWARD
TURN_RIGHT
make_step
LOOK_FORWARD
GO_STRAIGHT
make_step
LOOK_FORWARD
GO_STRAIGHT
make_step
LOOK_FORWARD
TURN_LEFT
make_step
LOOK_FORWARD
GO_STRAIGHTIn other words, NPI knows what high level operations call to what low/high level operations, but doesn't know how those high level operations choose what to call in which setting. We want NPI by observing those execution traces to learn to execute programs in new unseen settings of the environment.
Importantly, we do not expect NPI to produce the original program that was used to generate execution traces with all the branches and loops. Rather, we want NPI to execute programs directly, but producing traces that have the same structure as the traces that were shown to NPI during training. For example, look at the far right block on the image above, where NPI emits high level operations for addition. It emits the same high level operations that the original program would have emitted, and then the same low level operations for each of them, but it is unknown how exactly it decides what operation to emit when, the actual program is not produced.
How is NPI trained?
An NPI is a recurrent neural network. A recurrent neural network is a model that learns an approximation of a function that gets a sequence of varying length as an input, and produces a sequence of the same length as an output. In its simplest form a single step of a recurrent neural network is defined as a function:
def step(X, H):
Y_out = tanh(A1 * (X + H) + b1)
H_out = tanh(A2 * (X + H) + b2)
return Y_out, H_outHere X is the input at the corresponding timestep, and H is the value of H_out from the previous step. Before the first timestamp H is initialized to some default value, such as all zeros. Y_out is the value computed for the current time step. It is important to notice that Y at a particular step only depends on Xs up to that timestep, and that the function that computes Y is differentiable with respect to all As and bs, so those parameters can be learned with back propagation.
Such a simple recurrent neural network has many shortcomings, one most important one is that the gradient of Y with respect to parameters goes to zero very quickly as we go back across timestamps, and as such long term dependencies cannot be learned in any reasonable time. This problem is solved by more sophisticated step functions, two most widely used are LSTM (long-short term memory) and GRU (gated recurrent units). Importantly, while the actual way Y_out and H_out are computed in LSTMs and GRUs differ from the above step function, conceptually they are the same in the sense that they take the current X and the previous hidden state H as input, and produce Y and the new value of H as an output.
NPI, in particular, uses LSTM cells to avoid the vanishing gradient problem. The input to the NPI's LSTM at each timestamp is the observation of the environment (such as the full state of the grid with all the cursor positions for the addition problem), as well as some representation of the high level operation that is being executed. The output is either a low-level operation to be executed, a high-level operation to be executed, or an indication to stop. If it's a low-level operation, it is immediately executed in the environment, and the NPI moves to the next timestamp, feeding the new state of the environment as the input. If it's an indication to stop, the execution of the current high level operation is terminated.
If LSTM, however, has emitted a high level operation, the execution is more complex. First, NPI remembers the value of the hidden state H after the current timestamp was evaluated, let's call it h_last. Then a brand new LSTM is initialized, and is fed h_last as its initial value of H. This LSTM is then used to recursively execute the emitted high level operation. When the newly created LSTM finally terminates, its final hidden state value is discarded, the original LSTM is resumed again, and executes it's next timestamp, receiving h_last as the hidden state.
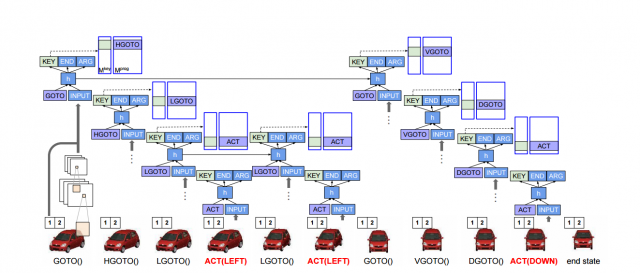
The overall architecture is shown in this picture:
When the NPI is trained, the emitted low-level or high-level operation is compared to that produced by the actual program to be learned, and if they do not match, the NPI is penalized. Whenever NPI fails to properly predict the operation to be executed during training, there's a question whether we should execute in the environment the correct operation from the actual execution trace we are feeding, or the operation that the NPI predicted. The motivation behind executing the correct operation is that if we feed predicted operations (which early on during training are mostly meaningless), the error in the environment accumulates, and the NPI has no chance of predicting consecutive operations correctly. The motivation behind feeding the predicted operations is that after the NPI is trained, during evaluation it will always be fed the predicted operations (since the correct ones are not known), and so feeding the correct ones during training makes the model to be trained in a setting that is different from the setting in which it will be evaluated. While there's a good technique that addresses this issue called Scheduled Sampling, NPI doesn't use it, and always executes the correct operation in the environment during training, disregarding the predicted one.
In the original paper the NPIs are tested on several toy tasks, including the addition described above, as well as a car rotation problem where the input to the neural network is an image of a car, and the network needs to bring it into a specific state via a sequence of rotate and shift operations:

With both toy tasks NPI achieves nearly perfect success rate. However, NPIs are rather impractical, since one needs the execution traces to train them, meaning that one needs to write the program himself before being able to learn it. Other models such as Neural Turing Machines are more interesting from this perspective, since they can be trained from input-output pairs, so one doesn't need to have an already working program. I will talk about Neural Turing Machines, and their more advanced version Neural Differentiable Computer, in one of the next posts in this series.
Provably correct NPIs and Recursion
One of the problems with NPIs is that we can only measure the generalization by running the trained NPI on various environments and observing the results. We can't, however, prove that the trained NPI perfectly generalizes even if we observe 100% generalization on some sample environments.
For example, in the case of multidigit addition the NPI might internally learn to execute a loop and add corresponding digits, however over time a small error in its hidden state can accumulate and result in errors after many thousands of digits.
A new paper that was presented on ICLR 2017 called Making Neural Programming Architecture Generalize Via Recursion addresses this issue by replacing loops in the programs used to generate execution traces with recursion. Fundamentally nothing in the NPI architecture prevents one from using recursion -- during the execution of a high level operation A the LSTM can theoretically emit the same high level operation, or some other high level operation B that in turn emits A. In other words, the model used in the 2017 paper is identical to the model used in the original Scott Reed's paper, the difference is only in the programs used to generate the execution traces. Since in the new paper the execution traces are generated by programs that contain no loops, execution of any high level operation under perfect generalization should yield a bounded number of steps, which means that we can prove that the trained NPI has generalized perfectly by induction if we can show that it emits correct low level commands for all the base cases, and emits correct bounded sequences of high and low level commands for all possible states of relevant part of the environment.
For example, in the example of multidigit addition, it is sufficient to show that the NPI properly terminates when no more digits are available (the environment has no digits under cursors and CARRY is zero), and that the NPI correctly adds up two numbers and recurses to itself for any pair of digits under cursor and state of the CARRY. Authors of the paper show that for recursive addition algorithm an NPI trained only on examples up to five digits long provably generalizes for arbitrarily long numbers.
Hope it was interesting. In the next post I will switch from learning how to execute programs to learning how to write them, and will show a nice demo of a recurrent neural network that tries to predict next few tokens as the programmer writes a program.
Hi, everybody,
A friend of mine and myself are working on a pet project that is attempting to train neural networks that can make sense of code and assist people with writing, reviewing and debugging it.
While there's a lot of data available on the Internet, such as huge open source projects, or all the solutions on Codeforces, there's also a lot of data missing, such as good alignment of code and what it does. We would like to get help from the community in labeling some of the missing data.
We allocated a certain budget to make some annotations to all CodeForces problems, as well as problems from other platforms, and are seeking people who are interested in spending some time on completing competitive-programming-related tasks for small compensation.
At this stage we are testing the labeling platform, so we would like to find 5-10 people with decent English writing skills who can allocate 30-60 minutes on 3-4 evenings this week to label some data (it will already be paid). If you are interested to participate, DM me or send me an email at [email protected].
Hi, everybody,
Drew Paroski, one of the creators of HHVM (JIT for PHP), who's currently working on MemSQL query compiler, will be giving a talk on August 19th in San Francisco on how to write compilers in modern C++.
Since many people are currently on internships in the Silicon Valley, I figured the event might be interesting to many people here, especially those who do systems programming.
The link to the event:
Round1
Problem B
The critical observation in this problem is that the points will be at the corners or very close to the corners. After that one simple solution would be to generate a set of all the points that are within 4 cells from some corner, and consider all quadruplets of points from that set.
Problem C
When the magician reveals the card, he has 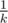 chance to reveal the same exact card that you have chosen. With the remaining
chance to reveal the same exact card that you have chosen. With the remaining 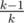 chance he will reveal some other card. Since all the cards in all m decks are equally likely to be in the n cards that he uses to perform the trick, he is equally likely to reveal any card among the n × m - 1 cards (-1 for the card that you have chosen, which we assume he has not revealed). There are only m - 1 cards that can be revealed that have the same value as the card you chose but are not the card you chose. Thus, the resulting probability is
chance he will reveal some other card. Since all the cards in all m decks are equally likely to be in the n cards that he uses to perform the trick, he is equally likely to reveal any card among the n × m - 1 cards (-1 for the card that you have chosen, which we assume he has not revealed). There are only m - 1 cards that can be revealed that have the same value as the card you chose but are not the card you chose. Thus, the resulting probability is 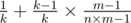
Problem D
One way to solve this problem is to maintain three deques, one per machine type, each one containing moments of time when the machines of this type will be available in increasing order. Originally each deck has as many zeroes, as many machines of that type are available. For each piece of laundry, see the earliest moment of time when each of the three machines will be available, and chose the time to put it in a washer in such a way, that there will be no delay when you move it to the dryer and to the folder. Remove the first elements from each of the deques, and push back moments of time when the piece of laundry you are processing is washed, dried and folded correspondingly. It can be shown that by doing that you will maintain all the deques sorted.
Problem E
This problem requires one to use one of the datastructures, such as suffix array, suffix tree or suffix automata. The easiest solution uses a compressed suffix tree. Build one suffix tree on all three strings. For simplicity add some non-alphabetic character at the end of each string. For every node in the tree store how many times the corresponding suffix occurs in each string. Then traverse the tree once. If the tree had no shortcuts, for every node that is a characters away from the root you would have increased the answer for a by the product of numbers of occurrences of the suffix in each of the strings. Since you do have shortcuts, you need to update the answer for all the lengths from a to b, where a and b are the distances of two ends of the shortcut from the root. One way to do it with constant time updates and linear time to print all the answers is the following. If the array of answers is v, then instead of computing v we can compute the array of differences p, such that pi = vi - vi - 1. This way when you traverse the shortcut, rather than adding some value at all the positions from a to b, you only need to add that value at position a, and subtract it at position b. When p is computed, it is easy to restore v in one pass.
Problem F
There are at least two different ways to solve this problem
First way is to notice that almost all the permutations have such numbers a and b. Consider solving the opposite problem: given n, build a permutation such that no subsequence of length 3 forms an arithmetic progression. One way to do that is to solve similar problem recursively for odd and even elements and concatenate the answer, i.e. solve it for  , and then form the answer for n as all the elements of the solution for
, and then form the answer for n as all the elements of the solution for  multiplied by two, followed by those elements multiplied by two minus one. This way we first place all the even numbers of the sequence, and then all the odd or vice versa.
multiplied by two, followed by those elements multiplied by two minus one. This way we first place all the even numbers of the sequence, and then all the odd or vice versa.
Now one observation that can be made is that all the permutations that don’t have a subsequence of length 3 that is an arithmetic progression are similar, with may be several elements in the middle being mixed up. As a matter of fact, it can be proven that the farthest distance an odd number can have from the odd half (or even number can have from the even part) is 6. With this knowledge we can build simple divide and conquer solution. If n < = 20, use brute force solution, otherwise, if the first and the last elements have the same remainder after division by two, then the answer is YES, otherwise, assuming without loss of generality that the first element is odd, if the distance from the first even element to the last odd element is more than 12, then the answer is YES, otherwise one can just recursively check all the odd elements separately, all the even elements separately, and then consider triplets of numbers, where one number is either in the odd or even part, and two numbers are among the at most 12 elements in the middle. This solution works in nlog(n) time. Another approach, that does not rely on the observation above, is to consider elements one by one, from left to right, maintaining a bitmask of all the numbers we’ve seen so far. If the current element we are considering is a, then for every element a - k that we saw, if we didn’t see a + k (assuming both a - k and a + k are between 0 and n - 1), then the answer is YES. Note that a - k was seen and a + k was not seen for some k if and only if the bitmask is not a palindrome with a center at a. To verify if it is a palindrome or not one can use polynomial hashes, making the complexity to be n × log(n).
Round 2
Problem A
The important observation one needs to make is that qn = qn - 1 + qn - 2, which means that we can replace two consecutive ‘1’ digits with one higher significance digit without changing the value. Note that sometimes the next digit may become more than ‘1’, but that doesn’t affect the solution.
There are two different kinds of solutions for this problem
The first kind of solution involves normalizing both numbers first. The normalization itself can be done in two ways — from the least significant digit or from the highest significant one using the replacement operation mentioned above. In either we will need O(n) operations for each number and we then just need to compare them lexicographically.
Other kind of solutions compare numbers digit by digit. We can start from the highest digit of the numbers, and propagate them to the lower digits. On each step we can do the following:
If both numbers have ones in the highest bit, then we can replace both ones with zeroes, and move on to the next highest bit.
Now only one number has one in the highest bit. Without loss of generality let’s say it’s the first number. We subtract one from the highest bit, and add it to the next two highest bits. Now the next two bits of the first number are at least as big as the first two bits of the second number. Let’s subtract the values of these two bits of the second number from both first and second number. By doing so we will make the next two bits of the second numbers become 0. If first number has at least one two, then it is most certainly bigger (because the sum of all the qi for i from 0 to n is smaller than twice qn + 1). Otherwise we still have only $0$s and $1$s, and can move on to the next highest bit, back to step (1). Since the ordinal of the highest bit is now smaller, and we only spent constant amount of time, the complexity of the algorithm is linear.
Problem B
One of the optimal strategies in this problem is to locate a node a with the most rows, then move all the data from the cluster a does not belong to onto a, and then for every other node b in the cluster that a belongs to either move all the data from b onto a, or move all the rows from the other cluster into b, whichever is cheaper.
Problem C
First let’s consider a subproblem in which we know how many votes we will have at the end, and we want to figure out how much money we will spend. To solve this problem, one first needs to buy the cheapest votes from all the candidates who have as many or more votes. If after that we still don’t have enough votes, we buy the cheapest votes overall from the remaining pool of votes until we have enough votes. Both can be done in linear time, if we maintain proper sorted lists of votes. This approach itself leads to an O(n2) solution. There are two ways of improving it. One is to come up with a way of computing the answer for k + 1 votes based on the answer for k votes. If for each number of votes we have a list of candidates, who have at least that many votes, and we also maintain a set of all the votes that are available for sale, then to move from k to k + 1 we first need to return the k-th most expensive vote for each candidate that has at least k votes (we had to buy them before, but now we do not have to anymore) back into the pool, and then get that many plus one votes from the pool (that many to cover votes we just returned, plus one because now we need k + 1 votes, not k). This solution has nlogn complexity, if we use a priority queue to maintain the pool of the cheapest votes. In fact, with certain tweaks one can reduce the complexity of moving from k to k + 1 to amortized constant, but the overall complexity will not improve, since one still needs to sort all the candidates at the beginning.
Another approach is to notice that the answer for the problem first strictly decreases with the number of votes we want to buy, and then strictly increases, so one can use ternary search to find the number of votes that minimizes the cost.
Problem D
The score function of a board in the problem is 2x, where x is number of rows and columns fully covered. Since 2x is the number of all the subsets of a set of size x (including both a full set and an empty set), the score function is essentially the number of ways to select a set of fully covered rows and columns on the board. The problem reduces to computing the expected number of such sets. For a given set of rows R and a given set of columns C we define pR, C as a probability that those rows and columns are fully covered. Then the answer is 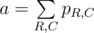 . For two sets of rows of the same size r and two sets of columns of the same size c the value of pR, C will be the same, let’s call it qr, c. With that observation the answer can be computed as
. For two sets of rows of the same size r and two sets of columns of the same size c the value of pR, C will be the same, let’s call it qr, c. With that observation the answer can be computed as 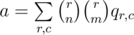 . qr, c in turn is just the probability that n(r + c) - rc numbers on the board are chosen from the k numbers that were called, and the remaining (n - c)(n - r) numbers on the board are chosen from the remaining m - (n(r + c) - rc) numbers available.
. qr, c in turn is just the probability that n(r + c) - rc numbers on the board are chosen from the k numbers that were called, and the remaining (n - c)(n - r) numbers on the board are chosen from the remaining m - (n(r + c) - rc) numbers available.
Problem E
Let’s begin by considering an arbitrary cycle in the given graph (if one exists). We could add some amount of flow to each edge in the cycle, and doing so must result in an equivalent or worse cost (otherwise the intern’s solution would clearly be non-optimal). Thus if we consider the function c(x) = sum(w_i * (f_i + x)^2), it should be minimized at x=0. Since this function is continuous, a necessary condition is c’(0) = 0. This implies sum(w_i * f_i) = 0 for any cycle.
Let us denote w_i * f_i as the “potential” of an edge. We can define the potential between two vertices in the same connected component as the sum of the potentials of the edges along any path between them. If the potential is not well defined, then the intern’s solution is not optimal. Additionally, the potential from node 1 to any other node must be positive (It cannot be zero because the original graph is biconnected), and similarly the potential from any node to node N must be positive. Furthermore no potential can exceed or equal the potential between node 1 and node N (if they are connected). These conditions can be verified in linear time using a dfs, allowing us to binary search the answer in O(N log N). Alternatively, the union-find algorithm can be modified to track potentials as well as components.
The true nature of the problem is revealed by making the following replacements:
weight -> resistance
bandwidth -> current
cost -> power
potential -> voltage
The problem asks you to determine if the given currents in a resistor network are optimal.
Problem F
The solution for this problem is a dynamic programming on a tree with O(n) complexity.
In this editorial “even tree” means a tree in which players will make an even number of turns, while “odd tree” is the tree in which players will make an odd number of turns.
We will be solving a slightly modified problem: one in which all the numbers on the leaves are $0$s and $1$s. Once this problem is solved, the general problem can be solved by doing a binary search on the answer, and then marking all the leaves with higher or equal value as $1$s, and all other values as $0$s.
If the tree is an odd tree, then the first player makes the last turn, and it is enough that at that moment only one of the two children of the root is 1. If the tree is an even tree, then the second player makes the last turn, so for the first player it is critical that by that time both children of the tree are 1 if he wants to win.
One simple case is the case when the tree is an odd tree, and both its immediate subtrees are even trees (by an immediate subtree, or just “subtree‘ of a node, here we will mean a subtree rooted at one of the nodes' immediate children).
In this case we can recursively solve each of the immediate subtrees, and if the first player wins any of them, he wins the entire tree. He does that by making his first turn into the tree that he can win, and then every time the second player makes a turn in that tree, responding with a corresponding optimal move, and every time the second player makes a turn in the other tree, making a random move there.
If both immediate subtrees are odd trees, however, a similar logic will not work. If the second player sees that the first player can win one of the trees, and the first player already made a turn in that tree, the second player can force the first player to play in the other tree, in which the second player will make the last turn, after which the first player will be forced to make a turn in the first tree, effectively making himself do two consecutive turns there. So to win the game the first player needs to be able to win a tree even if the second player has an option to skip one turn.
So we will need a second dimension to the dynamic programming solution that will indicate whether one of the players can skip one turn or not (we call the two states “canskip” if one can skip a turn and “noskip‘ if such an option does not exist). It can be easily shown, that we don’t need to store how many turns can be skipped, since if two turns can be skipped, and it benefits one player to skip a turn, another player will immediately use another skip, effectively making skips useless.
To make the terminology easier, we will use a term “we” to describe the first player, and “he” to describe the second player. “we can win a subtree” means that we can win it, if we go first there, “he can win a subtree” means that he can win it if he goes first (so “if one goes first” is always assumed and omitted). If we want to say that “we can win going second”, we will instead say “he cannot win [going first]” or “he loses [going first]”, which has the same meaning
Now we need to consider six cases (three possible parities of children multiplied by whether one can skip a turn or not). In all cases we assume that both children have at least two turns in them left. Cases when a child has no turns left (it is a leaf node), or when it has only one turn left (it is a node whose both children are leaves) are both corner cases and need to be handled separately. It is also important to note, that when one starts handling those corner cases, he will encounter an extra state, when the players have to skip a turn, even if it is not beneficial for whomever will be forced to do that. We call such state “forceskip”. In the case when both subtrees have more than one turn left, forceskip and canskip are the same, since players can always agree to play in such a way, that the skip, if available, is used, without changing the outcome. Below we only describe canskip and noskip cases, in terms of transitions from canskip and noskip states. One will need, however, to introduce forceskip state when he handles corner cases, which we do not describe in this editorial. The answer for forceskip will be the same as the answer for skip in general case, but different for corner cases.
even-even-noskip: the easiest case, described above, it is enough if we win any of the subtrees with no skip.
even-even-canskip: this case is similar to a case when there’s one odd subtree and one even subtree, and there’s no skip (the skip can be just considered as an extra turn attached to one of the trees), so the transition is similar to the one for odd-even-noskip case described below. We win iff we can win one tree with canskip, and he cannot win the other with noskip.
odd-even-noskip: if we can win the odd tree without a skip, and he cannot win the even tree without a skip, then we make a turn into the odd tree, and bring it into the even-even-noskip case, where he loses both trees, so we win. The other, less trivial, condition under which we win is If we can win the even tree with canskip, and he can’t win the odd tree with canskip. A motivation for this case is that odd subtree with a skip is similar to an even subtree, so by making a turn into the even case, we bring our opponent to an odd-odd case, where he loses both threes with a skip, which means that no matter which tree he makes a turn into, we will be responding to that tree, and even if he uses another tree to make a skip, he will still lose the tree into which he made his first turn. Since we make the last move, we win.
odd-even-skip: this is a simple case. We can consider the skip as an extra turn in the odd subtree, so as long as we can win even subtree with no skip, or odd subtree with a skip, we win.
odd-odd-noskip: we need to win either of the subtrees with a skip to win.
odd-odd-skip: to handle this case we can first consider immediately skipping: if he loses noskip case for the current subtree, then we win. Otherwise we win iff we can win one of trees with a skip, and he can’t win the other without a skip.
The more detailed motivation for each of the cases is left as an exercise.
Hello everyone!
The second round of MemSQL Start[c]UP 2.0 will take place today, August, 10th, 10:00am PDT. There will be two contests running simultaneously, one for people who participate onsite, and one for everybody else who advanced to the round two. Both rounds share the problemset and are rated based on the combined scoreboard.
Onsite participants will have special prizes for first three places. All onsite participants as well as the top 100 in the online contest will receive a start[c]up t-shirt.
People who have not advanced to the round two can participate in the round unofficially. Unofficial participation will be rated.
The contest will be 3 hours long, and will feature 6 problems. The score distribution is 1000-1000-1500-2000-2500-3000.
Good luck and happy coding!
UPDATE: final results will be delayed.
MemSQL is excited to announce Start[c]UP 2.0 – the second annual programming competition hosted by Codeforces with an onsite at MemSQL HQ in San Francisco, California.
Start[c]UP 2.0 consists of two rounds. Round 1 is online and takes place on July 27th at 10:00 AM PST. Round 1 follows regular Codeforces rules and consists of 5 problems. For this round, the complexity of the problems will be comparable to a regular Codeforces round. There are no eligibility restrictions to participate in the round. The round will be 2.5 hours long, and will be rated.
Round 2 takes place on August 10th at 10:00 AM PST, consists of 6 problems, and uses regular Codeforces rules. The complexity of the problems is higher than a regular Codeforces round, the round will be 3 hours long, and will be rated. Only people who finished in the top 500 in Round 1 can participate. The top 100 in round 2 will receive a Start[c]UP 2.0 T-shirt.
For Silicon Valley residents, MemSQL will be hosting up to 25 people on-site during the second round. The winner of the on-site round will be awarded a special prize.
UPDATE: first round will feature 6 problems, not five as it was announced earlier.
Hello everyone!
The second round of MemSQL start[c]up will take place on August, 3rd, 10:00am PDT. There will be two contests running simultaneously, one for people who participate onsite, and one for everybody else who advanced to the round two. Both rounds share the problemset and are rated based on the combined scoreboard.
Onsite participants will have special prizes for first three places. All onsite participants as well as the top 100 in the online contest will receive a start[c]up t-shirt.
People who have not advanced to the round two can participate in the round unofficially. Unofficial participation will be rated.
The contest will be 3 hours long, and will feature 6 problems. The score distribution is 500-1000-1000-2000-2500-3000.
The problem set has been developed by MemSQL engineers pieguy, nika, exod40, SkidanovAlex and dolphinigle.
Good luck and happy coding!
UPDATE: Editorial is up!
Author: AlexSkidanov
What happens if the rectangles form an N × N square? Then these two conditions are necessary.
1) The area must be exactly N × N.
2) The length of its sides must be N. That means, the difference between the right side of the rightmost rectangle — the left side of the leftmost rectangle is N. Same for topmost and bottommost rectangles.
We claim that, since the rectangles do not intersect, those two conditions are also sufficient.
This is since if there are only N × N space inside the box bounded by the leftmost, rightmost, topmost, and bottommost rectangles.
Thus if the sum of the area is exactly N × N, all space must be filled -- which forms a square.
Author: nika
Suppose the "divide-by-two" stage happens exactly D times, and the round robin happens with M people.
Then, the number of games held is: 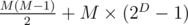
We would like that 
This is an equation with two variables -- to solve it, we can enumerate the value of one of the variables and calculate the value of the other one. We cannot enumerate the possible values of M, since M can vary from 1 to 10^9. However, we can enumerate D, since the number scales exponentially with D -- that is, we should only enumerate 0 ≤ D ≤ 62.
Thus, the equation is reduced to 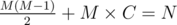
Since this function is increasing, this can be solved via binary search on M.
Author: AlexSkidanov
First part of the problem is to find minimum number of diamonds one can achieve by starting with a given monster. To do so, we will be using Dijkstra algorithm. Originally we don't know the minimum for any monster. For every rule we will maintain how many monsters with unknown minimums it has (let's call it ki for the i-th rule). Let's take every rule that has only diamonds in it (i.e. which has ki = 0), and assign number of diamonds in that rule as a tentative minimum for the monster (if a monster has several diamonds-only rules, take the smallest one). Then take the monster, that has the smallest tentative minimum currently assigned. For that monster the tentative value is the actual minimum due to the same reasoning we use when we prove correctness of Dijkstra algorithm. Now, since we know the minimum for that monster, for every rule i that has that monster in its result subtract 1 from ki for every occurrence of the monster in the result of that rule. If for any rule the value of ki becomes zero, update the tentative minimum for the monster that rule belongs to with the sum of minimum values for each monster that rule generates plus the number of diamonds that rule generates. Then from all the monsters for which we don't known the minimum yet, but for which we know the tentative minimum, pick the one with the smallest tentative minimum, and continue on.
At the end we will end up in a state, when each monster either has an actual minimum value assigned, or has no tentative value assigned. The latter monsters will have - 1 - 1 as their answer. For the former monsters we know the minimum, but don't know the maximum yet.
The second part of the problem is to find all the rules, after applying which we are guaranteed to never get rid of all the monsters. We will call such a rule bad. It is easy to show, that the rule bad if and only if it generates at least one monster with minimum value of -1. Remove all the bad rules from the set of rules.
When bad rules are removed, finding maximums is trivial. Starting from every node for which maximum is not assigned yet, we traverse all the monsters in a DFS order. For a given monster, we consider every rule. For a given rule, for each monster it generates, we call DFS to find its maximum value, and then sum them up, add number of diamonds for the rule, and check if this rule gives bigger max value than the one currently known for the monster. If we ever call DFS for a monster, for which we already have a DFS call on the stack, that means that that monster has some way of producing itself (directly or indirectly) and some non-zero number of diamonds (this is why problem statement has a constraint that every rule generates at least one diamond), so the answer for the monster is -2. If, processing any rule, we encounter a monster with max value -2, we immediately assign -2 as a max value for the monster the rule belongs to and return from the DFS.
As an exercise, think of a solution for the same problem, if rules are not guarantee to have at least one diamond in them.
Author: dolphinigle
Assume there's an extra sea cells on a row above the topmost row, and a row below the bottom most row. Hence, we can assume that the top and bottom row consists entirely of sea.
We claim that: There does not exist a sea route if and only if there exists a sequence of land cells that circumfere the planet (2 cells are adjacent if they share at least one point).
The "sufficient" part of the proof is easy -- since there exists such a sequence, it separates the sea into the northern and southern hemisphere and this forms a barrier disallowing passage between the two.
The "necessary" part. Suppose there does not exist such route. Then, if you perform a flood fill from any of the sea cell in the top row, you obtain a set of sea cells.
Trace the southern boundary of these set of cells, and you obtain the sequence of land circumfering the planet.
Thus, the algorithm works by simulating the reclamations one by one. Each time a land is going to be reclamated, we check if it would create a circumefering sequence. We will show that there's a way to do this check very quickly -- thus the algorithm should work within the time limit.
Stick two copies of the grid together side-by-side, forming a Rx(2*C) grid. The leftmost and rightmost cells of any row in this new grid are also adjacent, similar to the given grid.
Each time we're going to reclamate a land in row r and column c, we check if by doing so we would create a path going from (r, c) to (r, c + C). If it would, then we cancel the reclamation. Otherwise, we perform it, and add a land in cell (r, c) and (r, c+C).
This "is there a path from node X to node Y" queries can be answered very very quickly using union find -- we check whether is it possible to go from one of the 8 neighbors of (r, c) to one of the 8 neighbors of (r, c+C).
Correctness follows from the following: There exists a circumefering sequence IFF there exists a path from (r, c) to (r, c+C). Sufficient is easy. Suppose there exist a path from (r, c) to (r, c+C). We can form our circumfering sequence by overlapping the path from (r, c) to (r, c+C) with the same path, but going from (r, c+C) to (r, c) (we can do this since the grid is a two copies of the same grid sticked together).
Necessary. Suppose there exists a circumfering sequence. We claim that there must exist a path to go from (r, c) to (r, c+C). Consider the concatenation of an infinite number of our initial grid, forming an Rx(infinite * C) grid. If there exists a circumfering sequence, we claim that within this grid, there exists a path from (r, c) to (r, c+C).
Suppose there does not exist such a path. Since there exists a circumfering sequence, it must be possible to go from (r, c) to (r, c+ t * C), where t is an integer >= 2. Now, you should overlap all the paths taken to go from (r, c) to (r, c+t*C) in the grid (r', c' + C) (the grid immediately to the right of the grid where (r, c) is located). There must be a path from (r, c) to (r, c+C) in this new overlapped path.
Proofing the final part is difficult without interactive illustration -- basically since t >= 2, there exists a path that goes from the left side to the right side of the grid (r', c' + C). This path must intersect with one of the overlapping paths, and that path must be connected to (r, c+C). The details are left as... exercise :p.
Author: nika
In this part of editorial, all numbers we speak are in modulo N. So, if I say 10, it actually means 10 modulo N.
First, observe that this problem asks us to find a cycle that visits each node exactly once, i.e., a hamiltonian cycle. Thus, for each node X, there exists one other node that we used to go to node X, and one node that we visit after node X. We call them bef(X) and aft(X) (shorthand for before and after).
First we will show that if N is odd, then the answer is - 1.
Proof...? Consider node 0. What nodes points to node 0? Such node H must satisfy either of the following conditions:
2H = 0
2H + 1 = 0
The first condition is satisfied only by H = 0. The second condition is satisfied only by one value of H: floor(N / 2).
So, since we need a hamiltonian cycle, pre[0] must be floor(N/2), and aft[floor(N/2)] = 0
Now, consider node N - 1. What nodes points to node N - 1?
2H = N - 1
2H + 1 = N - 1
The second condition is satisfied only by H = N - 1. The first condition is satisfied only by H = floor(N / 2)
But we need a hamiltonian cycle, so aft[floor(N/2)] must be N - 1. This is a contradiction with that aft[floor(N/2)] must be 0.
Now, N is even. This case is much more interesting.
Consider a node X. It is connected to 2X and 2X + 1. Consider the node X + N / 2. It is connected to 2X + N and 2X + 1 + N, which reduces to 2X and 2X + 1.
So, apparently node X and node X + N / 2 are connected to the same set of values.
Now, notice that each node X will have exactly two nodes pointing to it. This is since such node H must satisfy
2H = X
2H + 1 = X
modulo N, each of those two equations have exactly one solution.
So, this combined with that node X and X + N / 2 have the same set of connected nodes means that the only way to go to node 2X or 2X + 1 is from nodes X and X + N / 2.
Thus, if you choose to go from node X to node 2X, you HAVE to go from node X + N / 2 to node 2X + 1 (or vice versa).
Now, try to follow the rule above and generate any such configuration. This configuration will consists of cycles, possibly more than 1. Can we join them into a single large cycle, visiting all nodes?
Yes we can, since those cycles are special.
Weird theorem: If there are 2 + cycles, then there must exist X and such node X and node X + N / 2 are in different cycles.
Proof: Suppose not. We show that there must exist one cycle in that case. Since node X and X + N / 2 are in the same cycle, they must also be in the same cycle as node 2X and 2X + 1. In particular, node X and 2X and 2X + 1 are all in the same cycle. It is possible to go from any node X to any node Y by following this pattern (left as exercise). Now, consider the X such that node X and node X + N / 2 are in different cycles. Suppose we go from node X to node 2X + A, and from X + N / 2 to 2X + B (such that A + B = 1). Switch the route -- we go from node X to 2X + B and X + N / 2 to 2X + A instead. This will merge the two cycles -- very similar to how we merge two cycles when finding an eulerian path. Thus, we can keep doing this to obtain our cycle!
...It's not entirely obvious to do that in O(N) time. An example solution: use DFS. DFS from node 0. For each node X:
if it has been visited, return
if X + N / 2 has been visited, go to either 2X or 2X + 1 and recurse, depending on which route used by node X + N / 2
otherwise, we go to node 2X and recurse. Then, check if X + N / 2 was visited in the recursion. If it was not, then the two of them forms two different cycles. We merge them by switching our route to 2X + 1 instead, and recurse again.
Hello everyone!
The first round of start[c]up is upon us. It is open to all participants. Registration works as a normal CodeForces round, and will close five minutes before the start of the contest.
The contest uses normal Codeforces rules, and will be rated. The score distribution is 500-1000-2000-2000-2500.
The problem set has been developed by MemSQL engineers pieguy, nika, exod40, SkidanovAlex and dolphinigle.
Top 500 competitors will advance to the second round, with the top 25 Silicon Valley residents invited to participate on-site, where there will be special prizes.
Good luck and happy coding!
UPDATE: Please note that the score distribution has changed.
UPDATE: Editorial is up now!
MemSQL is happy to announce start[c]up -- a programming competition, hosted by Codeforces and MemSQL HQ located in San Francisco, California. start[c]up consists of two rounds.
All rounds will be prepared by MemSQL engineers: pieguy, nika, exod40, SkidanovAlex and dolphinigle.
Round 1 is online and takes place on July 13. Round 1 follows regular Codeforces rules and consists of 5 problems. For this round, the complexity of the problems will be comparable to a regular Codeforces round. There are no eligibility restrictions to participate in the round.
Round 2 takes place on August 3, consists of 5 problems, and uses regular Codeforces rules. The complexity of the problems is higher than a regular Codeforces round. Only people who finished in the top 500 in Round 1 can participate. The top 100 in round 2 will receive a start[c]up T-shirt.
For the Silicon Valley residents, MemSQL will be hosting up to 25 people on-site during the second round. The winner of the on-site round will be awarded a special prize.
MemSQL is building an in-memory database that powers many well-known companies, such as Morgan Stanley and Zynga. Nearly half of our engineers are TopCoder Open Algorithm finalists in recent years, and we have more IOI and ICPC medals than we have engineers.
The reason for such a skew towards topcoders is that only very good engineers can build a database. Even though topcoders might not have skills necessary to build a database, they are known to be very smart. We’ve seen that smart coders can quickly acquire necessary skills, but average coders, regardless of experience, cannot learn to be smart.
We have lots of exciting problems for topcoders. For example SQL Query optimizer, cluster management for the distributed system, lockfree storage engine were all written by topcoders in here. If you are looking for an internship or for a full-time position and want to work on exciting stuff with people who are as smart as yourself, send your resume to [email protected].
| Name |
|---|










