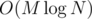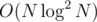Всем привет!
Сейчас решал задачу и тут понадобилось реализовать копирование декартова дерева, в частности у меня есть дерево T и его нужно скопировать и смержить в конец двух других деревьев. Возможно ли это сделать без обхода всего дерева?
UPD Пишу на указателях.











 , 2014
, 2014 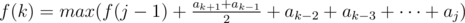 , если последний отрезочек —
, если последний отрезочек — 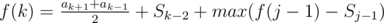 , где
, где