Editorial Round 1 of Yandex.Algorithm 2018

#	User	Rating
1	tourist	4009
2	jiangly	3823
3	Benq	3738
4	Radewoosh	3633
5	jqdai0815	3620
6	orzdevinwang	3529
7	ecnerwala	3446
8	Um_nik	3396
9	ksun48	3390
10	gamegame	3386

#	User	Contrib.
1	cry	167
2	Um_nik	163
3	maomao90	162
3	atcoder_official	162
5	adamant	159
6	-is-this-fft-	158
7	awoo	157
8	TheScrasse	154
9	Dominater069	153
9	nor	153

Police Patrol

Alphabetic Subsequence

We can check that this is equivalent to counting the number of permutations of 0, 1, 2, ..., 9 that appear in s.

There are two solutions:

solution 1

solution 2

Infinite Graph Game

Consider at each step, instead of adding our score to a global counter, we incremented the score at a particular vertex. So, we only need to simulate one round, and can multiply by an appropriate constant to get the limit value. We can also check the infinite case here (the contribution of a node is nonzero and it never gets chosen so its value never gets reduced).

The problem is that this approach takes O(nk) time in the worst case. Let's look at each edge individually. If node a appears f_a times, and node b appears f_b times in our sequence, we can get the contribution of this edge onto each node's values in O(f_a + f_b) time. We can also further reduce this to O(min(f_a, f_b) * log(max(f_a, f_b))) time by iterating through the explicit occurences of the node that appears fewer times, and using some data structures to count the number of occurences of the other node between any two explicit occurences.

With this reduction, this brings our running time to O(n * sqrt(n) * log(n)) (for example, see this problem for analysis: http://codeforces.net/problemset/problem/804/D)

c++ code

#include <cstdio>
#include <cassert>
#include <cstdlib>
#include <vector>
using namespace std;

const int MOD = 1000 * 1000 * 1000 + 7;

inline int add(int a, int b) {
    if ((a += b) >= MOD) {
        a -= MOD;
    }
    return a;
}

typedef long long llong;

inline int mul(int a, int b) {
    return ((llong)a) * b % MOD;
}

inline int sub(int a, int b) {
    if ((a -= b) < 0) {
        a += MOD;
    }
    return a;
}

int powmod(int a, int b) {
    int res = 1;
    while (b > 0) {
        if (b & 1) {
            res = mul(res, a);
        }
        a = mul(a, a);
        b >>= 1;
    }
    return res;
}

int inv(int x) {
    return powmod(x, MOD - 2);
}

const int N = 100500;

int V[N];

vector<int> history[N];

int AF[N];

void die() {
    puts("-1");
    exit(0);
}

int pw2[N];

int main() {
    int n, m, k;
    scanf("%d %d %d", &n, &m, &k);
    for (int i = 0; i < n; i++) {
        scanf("%d", &V[i]);
    }
    for (int i = 0; i < k; i++) {
        int s;
        scanf("%d", &s);
        --s;
        history[s].push_back(i);
    }
    pw2[0] = 1;
    for (int i = 0; i < k; i++) {
        pw2[i + 1] = (pw2[i] % 2 == 0) ? pw2[i] / 2 : (pw2[i] + MOD) / 2;
    }

    for (int i = 0; i < m; i++) {
        int a, b;
        scanf("%d %d", &a, &b);
        --a, --b;
        if (history[a].size() > history[b].size()) {
            swap(a, b);
        }
        if (history[b].empty()) {
            continue;
        } else if (history[a].empty()) {
            if (V[a] == 0) {
                continue;
            } else {
                die();
            }
        } else {
            int prv = 0;
            for (int i = 0; i < (int)history[a].size(); i++) {
                int x = history[a][i];
                int p = lower_bound(history[b].begin(), history[b].end(), x) - history[b].begin();
                AF[b] = add(AF[b], pw2[p]);
                AF[a] = add(AF[a], mul(p - prv, pw2[i]));
                prv = p;
            }
            AF[a] = add(AF[a], mul((int)history[b].size() - prv, pw2[(int)history[a].size()]));
        }
    }

    int ans = 0;

    for (int i = 0; i < n; i++) {
        if (AF[i] != 0) {
            assert(!history[i].empty());
        }
        int k = pw2[(int)history[i].size()];
        int num = mul(AF[i], V[i]);
        int den = sub(1, k);
        ans = add(ans, mul(num, inv(den)));
    }
    printf("%d\n", ans);
}

java code

import java.io.OutputStream;
import java.io.IOException;
import java.io.InputStream;
import java.io.OutputStream;
import java.io.PrintWriter;
import java.util.stream.Stream;
import java.io.BufferedWriter;
import java.io.Writer;
import java.io.OutputStreamWriter;
import java.util.InputMismatchException;
import java.io.IOException;
import java.util.Collections;
import java.util.ArrayList;
import java.io.InputStream;

/**
 * Built using CHelper plug-in
 * Actual solution is at the top
 */
public class Main {
    public static void main(String[] args) {
        InputStream inputStream = System.in;
        OutputStream outputStream = System.out;
        InputReader in = new InputReader(inputStream);
        OutputWriter out = new OutputWriter(outputStream);
        InfiniteGraphGame solver = new InfiniteGraphGame();
        solver.solve(1, in, out);
        out.close();
    }

    static class InfiniteGraphGame {
        public int mod = 1000000007;
        int[] cc;
        int[] sz;
        ArrayList<Integer>[] pos;

        public void solve(int testNumber, InputReader in, OutputWriter out) {
            int n = in.nextInt(), m = in.nextInt(), k = in.nextInt();
            int[] v = in.readIntArray(n);
            int[] s = in.readIntArray(k);
            for (int i = 0; i < k; i++) s[i]--;
            pos = Stream.generate(ArrayList::new).limit(n).toArray(ArrayList[]::new);
            for (int i = 0; i < n; i++) pos[i].add(0);
            cc = new int[k + 1];
            sz = new int[n];
            for (int i = 1; i <= k; i++) {
                cc[i] = pos[s[i - 1]].size();
                pos[s[i - 1]].add(i);
                sz[s[i - 1]]++;
            }

            long[] div2 = new long[k + 1];
            div2[0] = 1;
            long mult = Utils.inv(2, mod);
            for (int i = 1; i < div2.length; i++) {
                div2[i] = div2[i - 1] * mult % mod;
            }

            long ans = 0;
            for (int i = 0; i < m; i++) {
                int a = in.nextInt() - 1, b = in.nextInt() - 1;
                if (sz[a] > sz[b]) {
                    int t = a;
                    a = b;
                    b = t;
                }
                if (sz[b] > 0 && sz[a] == 0 && v[a] > 0) {
                    out.println(-1);
                    return;
                }

                long sa = 0, sb = 0;
                int da = 0, db = 0;
                int lastw = 0;
                for (int q : pos[a]) {
                    if (q == 0) continue;
                    int curw = cc[pos[b].get(-Collections.binarySearch(pos[b], q) - 2)];
                    long w = curw - lastw;
                    lastw = curw;

                    sa = (sa + 1L * w * v[a] % mod * div2[da]) % mod;
                    db += w;
                    sb = (sb + v[b] * div2[db]) % mod;
                    da++;
                }
                {
                    long w = sz[b] - lastw;
                    sa = (sa + 1L * w * v[a] % mod * div2[da]) % mod;
                    db += w;
                }

                sa = sa * Utils.inv(1 - div2[da] + mod, mod) % mod;
                sb = sb * Utils.inv(1 - div2[db] + mod, mod) % mod;
                ans = (ans + sa + sb) % mod;
            }
            out.println(ans);
        }

    }

    static class OutputWriter {
        private final PrintWriter writer;

        public OutputWriter(OutputStream outputStream) {
            writer = new PrintWriter(new BufferedWriter(new OutputStreamWriter(outputStream)));
        }

        public OutputWriter(Writer writer) {
            this.writer = new PrintWriter(writer);
        }

        public void close() {
            writer.close();
        }

        public void println(long i) {
            writer.println(i);
        }

        public void println(int i) {
            writer.println(i);
        }

    }

    static class InputReader {
        private InputStream stream;
        private byte[] buf = new byte[1 << 16];
        private int curChar;
        private int numChars;

        public InputReader(InputStream stream) {
            this.stream = stream;
        }

        public int[] readIntArray(int tokens) {
            int[] ret = new int[tokens];
            for (int i = 0; i < tokens; i++) {
                ret[i] = nextInt();
            }
            return ret;
        }

        public int read() {
            if (this.numChars == -1) {
                throw new InputMismatchException();
            } else {
                if (this.curChar >= this.numChars) {
                    this.curChar = 0;

                    try {
                        this.numChars = this.stream.read(this.buf);
                    } catch (IOException var2) {
                        throw new InputMismatchException();
                    }

                    if (this.numChars <= 0) {
                        return -1;
                    }
                }

                return this.buf[this.curChar++];
            }
        }

        public int nextInt() {
            int c;
            for (c = this.read(); isSpaceChar(c); c = this.read()) {
                ;
            }

            byte sgn = 1;
            if (c == 45) {
                sgn = -1;
                c = this.read();
            }

            int res = 0;

            while (c >= 48 && c <= 57) {
                res *= 10;
                res += c - 48;
                c = this.read();
                if (isSpaceChar(c)) {
                    return res * sgn;
                }
            }

            throw new InputMismatchException();
        }

        public static boolean isSpaceChar(int c) {
            return c == 32 || c == 10 || c == 13 || c == 9 || c == -1;
        }

    }

    static class Utils {
        public static long inv(long N, long M) {
            long x = 0, lastx = 1, y = 1, lasty = 0, q, t, a = N, b = M;
            while (b != 0) {
                q = a / b;
                t = a % b;
                a = b;
                b = t;
                t = x;
                x = lastx - q * x;
                lastx = t;
                t = y;
                y = lasty - q * y;
                lasty = t;
            }
            return (lastx + M) % M;
        }

    }
}

Stamp Stamp Stamp

The bounds might look a bit strange, and it was a bit hard to find good bounds for this. Originally, I wanted to set bounds higher so only O(n³·logn) solutions could pass, but it seems the constant factor for that solution is too high. So, I set bounds low enough so a O(n⁴) solution could pass as well.

O(n^4)

O(n^3 log n)

For an O(n³·logn) solution, consider all occurences of t in s (these can be found in O(|s| + |t|) time). Then, consider extending a region as far as we can left by prepending a prefix of t, and extending a region as far as we can to the right by appending a suffix of t. This can be done with a stack or segment trees. Then, we have a set of intervals, and we want to check it covers 1, ..., n. This can also be done in time after sorting. Note, there is some tricky case in that if there can be gaps between the intervals, but these gaps need to consist of substrings of t. This can also be checked in linear time using suffix automaton.

code

import java.io.OutputStream;
import java.io.IOException;
import java.io.InputStream;
import java.io.OutputStream;
import java.io.PrintWriter;
import java.util.Arrays;
import java.io.BufferedWriter;
import java.util.InputMismatchException;
import java.io.IOException;
import java.util.ArrayList;
import java.util.HashSet;
import java.util.List;
import java.io.Writer;
import java.io.OutputStreamWriter;
import java.util.Collections;
import java.io.InputStream;

/**
 * Built using CHelper plug-in
 * Actual solution is at the top
 */
public class Main2 {
    public static void main(String[] args) {
        InputStream inputStream = System.in;
        OutputStream outputStream = System.out;
        InputReader in = new InputReader(inputStream);
        OutputWriter out = new OutputWriter(outputStream);
        StampStampStamp solver = new StampStampStamp();
        solver.solve(1, in, out);
        out.close();
    }

    static class StampStampStamp {
        String s;
        SegmentTreeFast st;
        int[] r1;
        int[] r2;
        int[] left;
        int[] right;
        Pair<Integer, Integer>[] pp;

        public void solve(int testNumber, InputReader in, OutputWriter out) {
            s = in.next();
            int n = s.length();
            r1 = new int[n];
            r2 = new int[n];
            left = new int[n];
            right = new int[n];
            st = new SegmentTreeFast(n);
            pp = new Pair[n];
            HashSet<String> ss = new HashSet<>();
            HashSet<String> t = new HashSet<>();
            for (int i = 0; i < n; i++) {
                for (int j = i; j < n; j++) {
                    String test = s.substring(i, j + 1);
                    if (t.add(test) && ok(test, s)) {
                        ss.add(test);
                    }
                }
            }
            ArrayList<String> ans = new ArrayList<>(ss);
            Collections.sort(ans);
            for (String x : ans) out.println(x);
        }

        boolean ok(String sub, String all) {
            if (sub.charAt(0) != all.charAt(0) || sub.charAt(sub.length() - 1) != all.charAt(all.length() - 1))
                return false;
            HashSet<Character> tt = new HashSet<>();
            for (char k : sub.toCharArray()) tt.add(k);
            for (char k : all.toCharArray()) if (!tt.contains(k)) return false;
            char[] c1 = (sub + "*" + all).toCharArray();
            int[] z1 = ZAlgorithm.zAlgorithm(c1);
            char[] c2 = (new StringBuffer(sub).reverse().toString() + "*" +
                    new StringBuffer(all).reverse().toString()).toCharArray();
            int[] z2 = ZAlgorithm.zAlgorithm(c2);

            int m = sub.length();
            int n = all.length();
            st.clear();
            for (int i = n - 1; i >= 0; i--) {
                int z = z1[i + m + 1];
                if (z == 0) {
                    r1[i] = -1;
                } else {
                    r1[i] = Math.max(i + z - 1, st.query(i + 1, i + z));
                }
                st.modify(i, i, r1[i]);
                pp[i] = new Pair(-r1[i], i);
            }
            Arrays.sort(pp);
            int idx = 0;
            int min = n;
            for (int i = n - 1; i >= 0; i--) {
                while (idx < n && -pp[idx].u >= i) {
                    min = Math.min(min, pp[idx].v);
                    idx++;
                }
                left[i] = Math.min(min, i + 1);
            }

            st.clear();
            int[] right = new int[n];
            for (int i = 0; i < n; i++) {
                int z = z2[n - i - 1 + m + 1];
                if (z == 0) {
                    r2[i] = n + 1;
                } else {
                    r2[i] = Math.min(i - z + 1, -st.query(i - z, i - 1));
                }
                st.modify(i, i, -r2[i]);
                pp[i] = new Pair(r2[i], i);
            }
            Arrays.sort(pp);
            idx = 0;
            int max = -1;
            for (int i = 0; i < n; i++) {
                while (idx < n && pp[idx].u <= i) {
                    max = Math.max(max, pp[idx].v);
                    idx++;
                }
                right[i] = Math.max(i - 1, max);
            }

            ArrayList<Integer> evts = new ArrayList<>();

            for (int i = 0; i < n; i++) {
                if (z1[i + m + 1] == m) {
                    evts.add((i == 0 ? 0 : left[i - 1]) * 2 + 0);
                    evts.add(right[i] * 2 + 1);
                }
            }
            Collections.sort(evts);
            SuffixAutomaton.State[] automaton = SuffixAutomaton.buildSuffixAutomaton(sub);
            int psum = 0;
            for (int i = 0; i + 1 < evts.size(); i++) {
                int k = evts.get(i);
                if (k % 2 == 0) psum++;
                else psum--;
                if (psum == 0) {
                    int cur = k / 2 + 1;
                    int nxt = evts.get(i + 1) / 2;
                    int node = 0;
                    for (int j = cur; j < nxt; j++) {
                        int next = automaton[node].next[all.charAt(j)];
                        if (next == -1) return false;
                        node = next;
                    }
                }
            }
            return evts.get(0) / 2 == 0 && evts.get(evts.size() - 1) / 2 == n - 1;
        }

    }

    static class ZAlgorithm {
        public static int[] zAlgorithm(char[] let) {
            int N = let.length;
            int[] z = new int[N];
            int L = 0, R = 0;
            for (int i = 1; i < N; i++) {
                if (i > R) {
                    L = R = i;
                    while (R < N && let[R - L] == let[R])
                        R++;
                    z[i] = R - L;
                    R--;
                } else {
                    int k = i - L;
                    if (z[k] < R - i + 1)
                        z[i] = z[k];
                    else {
                        L = i;
                        while (R < N && let[R - L] == let[R])
                            R++;
                        z[i] = R - L;
                        R--;
                    }
                }
            }
            z[0] = N;
            return z;
        }

    }

    static class OutputWriter {
        private final PrintWriter writer;

        public OutputWriter(OutputStream outputStream) {
            writer = new PrintWriter(new BufferedWriter(new OutputStreamWriter(outputStream)));
        }

        public OutputWriter(Writer writer) {
            this.writer = new PrintWriter(writer);
        }

        public void print(Object... objects) {
            for (int i = 0; i < objects.length; i++) {
                if (i != 0) {
                    writer.print(' ');
                }
                writer.print(objects[i]);
            }
        }

        public void println(Object... objects) {
            print(objects);
            writer.println();
        }

        public void close() {
            writer.close();
        }

    }

    static class SuffixAutomaton {
        public static SuffixAutomaton.State[] buildSuffixAutomaton(CharSequence s) {
            int n = s.length();
            SuffixAutomaton.State[] st = new SuffixAutomaton.State[Math.max(2, 2 * n - 1)];
            st[0] = new SuffixAutomaton.State();
            st[0].suffLink = -1;
            int last = 0;
            int size = 1;
            for (int i = 0; i < s.length(); i++) {
                char c = s.charAt(i);
                int cur = size++;
                st[cur] = new SuffixAutomaton.State();
                st[cur].length = i + 1;
                st[cur].firstPos = i;
                int p = last;
                for (; p != -1 && st[p].next[c] == -1; p = st[p].suffLink) {
                    st[p].next[c] = cur;
                }
                if (p == -1) {
                    st[cur].suffLink = 0;
                } else {
                    int q = st[p].next[c];
                    if (st[p].length + 1 == st[q].length) {
                        st[cur].suffLink = q;
                    } else {
                        int clone = size++;
                        st[clone] = new SuffixAutomaton.State();
                        st[clone].length = st[p].length + 1;
                        System.arraycopy(st[q].next, 0, st[clone].next, 0, st[q].next.length);
                        st[clone].suffLink = st[q].suffLink;
                        for (; p != -1 && st[p].next[c] == q; p = st[p].suffLink) {
                            st[p].next[c] = clone;
                        }
                        st[q].suffLink = clone;
                        st[cur].suffLink = clone;
                    }
                }
                last = cur;
            }
            for (int i = 1; i < size; i++) {
                st[st[i].suffLink].invSuffLinks.add(i);
            }
            return Arrays.copyOf(st, size);
        }

        public static class State {
            public int length;
            public int suffLink;
            public List<Integer> invSuffLinks = new ArrayList<>(0);
            public int firstPos = -1;
            public int[] next = new int[128];

            {
                Arrays.fill(next, -1);
            }
        }

    }

    static class InputReader {
        private InputStream stream;
        private byte[] buf = new byte[1 << 16];
        private int curChar;
        private int numChars;

        public InputReader(InputStream stream) {
            this.stream = stream;
        }

        public int read() {
            if (this.numChars == -1) {
                throw new InputMismatchException();
            } else {
                if (this.curChar >= this.numChars) {
                    this.curChar = 0;

                    try {
                        this.numChars = this.stream.read(this.buf);
                    } catch (IOException var2) {
                        throw new InputMismatchException();
                    }

                    if (this.numChars <= 0) {
                        return -1;
                    }
                }

                return this.buf[this.curChar++];
            }
        }

        public String next() {
            int c;
            while (isSpaceChar(c = this.read())) {
                ;
            }

            StringBuilder result = new StringBuilder();
            result.appendCodePoint(c);

            while (!isSpaceChar(c = this.read())) {
                result.appendCodePoint(c);
            }

            return result.toString();
        }

        public static boolean isSpaceChar(int c) {
            return c == 32 || c == 10 || c == 13 || c == 9 || c == -1;
        }

    }

    static class SegmentTreeFast {
        int[] value;
        int[] delta;

        public SegmentTreeFast(int n) {
            value = new int[2 * n];
            for (int i = 0; i < n; i++) {
                value[i + n] = getInitValue();
            }
            for (int i = 2 * n - 1; i > 1; i -= 2) {
                value[i >> 1] = queryOperation(value[i], value[i ^ 1]);
            }
            delta = new int[2 * n];
            Arrays.fill(delta, getNeutralDelta());
        }

        public void clear() {
            int n = value.length / 2;
            for (int i = 0; i < n; i++) {
                value[i + n] = getInitValue();
            }
            for (int i = 2 * n - 1; i > 1; i -= 2) {
                value[i >> 1] = queryOperation(value[i], value[i ^ 1]);
            }
            Arrays.fill(delta, getNeutralDelta());
        }

        int modifyOperation(int x, int y) {
            return Math.max(x, y);
        }

        int queryOperation(int leftValue, int rightValue) {
            return Math.max(leftValue, rightValue);
        }

        int deltaEffectOnSegment(int delta, int segmentLength) {
            if (delta == getNeutralDelta()) return getNeutralDelta();
            // Here you must write a fast equivalent of following slow code:
            // int result = delta;
            // for (int i = 1; i < segmentLength; i++) result = queryOperation(result, delta);
            // return result;
            return delta;
//        return delta * segmentLength;
        }

        int getNeutralDelta() {
            return -(1 << 29);
        }

        int getInitValue() {
            return -(1 << 29);
        }

        int joinValueWithDelta(int value, int delta) {
            if (delta == getNeutralDelta()) return value;
            return modifyOperation(value, delta);
        }

        int joinDeltas(int delta1, int delta2) {
            if (delta1 == getNeutralDelta()) return delta2;
            if (delta2 == getNeutralDelta()) return delta1;
            return modifyOperation(delta1, delta2);
        }

        void pushDelta(int i) {
            int d = 0;
            for (; (i >> d) > 0; d++) {
            }
            for (d -= 2; d >= 0; d--) {
                int x = i >> d;
                value[x >> 1] = joinNodeValueWithDelta(x >> 1, 1 << (d + 1));
                delta[x] = joinDeltas(delta[x], delta[x >> 1]);
                delta[x ^ 1] = joinDeltas(delta[x ^ 1], delta[x >> 1]);
                delta[x >> 1] = getNeutralDelta();
            }
        }

        int joinNodeValueWithDelta(int i, int len) {
            return joinValueWithDelta(value[i], deltaEffectOnSegment(delta[i], len));
        }

        public int query(int from, int to) {
            to = Math.min(to, value.length / 2 - 1);
            from = Math.max(from, 0);
            if (to < from) return getInitValue();
            from += value.length >> 1;
            to += value.length >> 1;
            pushDelta(from);
            pushDelta(to);
            int res = 0;
            boolean found = false;
            for (int len = 1; from <= to; from = (from + 1) >> 1, to = (to - 1) >> 1, len <<= 1) {
                if ((from & 1) != 0) {
                    res = found ? queryOperation(res, joinNodeValueWithDelta(from, len)) : joinNodeValueWithDelta(from, len);
                    found = true;
                }
                if ((to & 1) == 0) {
                    res = found ? queryOperation(res, joinNodeValueWithDelta(to, len)) : joinNodeValueWithDelta(to, len);
                    found = true;
                }
            }
            if (!found) throw new RuntimeException();
            return res;
        }

        public void modify(int from, int to, int delta) {
            if (from > to) return;
            from += value.length >> 1;
            to += value.length >> 1;
            pushDelta(from);
            pushDelta(to);
            int a = from;
            int b = to;
            for (; from <= to; from = (from + 1) >> 1, to = (to - 1) >> 1) {
                if ((from & 1) != 0) {
                    this.delta[from] = joinDeltas(this.delta[from], delta);
                }
                if ((to & 1) == 0) {
                    this.delta[to] = joinDeltas(this.delta[to], delta);
                }
            }
            for (int i = a, len = 1; i > 1; i >>= 1, len <<= 1) {
                value[i >> 1] = queryOperation(joinNodeValueWithDelta(i, len), joinNodeValueWithDelta(i ^ 1, len));
            }
            for (int i = b, len = 1; i > 1; i >>= 1, len <<= 1) {
                value[i >> 1] = queryOperation(joinNodeValueWithDelta(i, len), joinNodeValueWithDelta(i ^ 1, len));
            }
        }

    }

    static class Pair<U extends Comparable<U>, V extends Comparable<V>> implements Comparable<Pair<U, V>> {
        public final U u;
        public final V v;

        public Pair(U u, V v) {
            this.u = u;
            this.v = v;
        }

        public int hashCode() {
            return (u == null ? 0 : u.hashCode() * 31) + (v == null ? 0 : v.hashCode());
        }

        public boolean equals(Object o) {
            if (this == o)
                return true;
            if (o == null || getClass() != o.getClass())
                return false;
            Pair<U, V> p = (Pair<U, V>) o;
            return (u == null ? p.u == null : u.equals(p.u)) && (v == null ? p.v == null : v.equals(p.v));
        }

        public int compareTo(Pair<U, V> b) {
            int cmpU = u.compareTo(b.u);
            return cmpU != 0 ? cmpU : v.compareTo(b.v);
        }

        public String toString() {
            return String.format("[Pair = (%s, %s)", u.toString(), v.toString());
        }

    }
}

Increasing Sequence

Be careful, it is not true in general that the set of valid k forms an interval. For example, consider this case [6, 4, 4, 6]. k = 7 works, by turning the array into [1, 3, 4, 6]. k = 9 works by turning the array into [3, 4, 5, 6]. But, k = 8 doesn't work since the middle two elements will stay the same.

Our solution will eliminate intervals of k that are bad if we choose to flip or not flip certain elements. Let F(i) be the set of intervals that is bad if we flip element i, and let T(i) be the set of intervals that is bad if we don't flip element i.

For each individual element, if we choose to flip it, and this adds the inequality x_i ≤ k, so this adds the bad interval [0, x_i - 1] to F(i).

For a pair of adjacent indices x_i, x_i + 1, we can check we can check what inequalities it imposes on k if we decide to flip or not flip certain elements (you can see the code for the exact cases).

After getting these bad intervals, it suffices to try to find some point such that this point is not in F(i) or not in T(i) for all i. This can be done with a line sweep.

code

#include <cstdio>
#include <algorithm>
#include <cstdlib>
#include <vector>
#include <cassert>
using namespace std;

const int N = 200500;

int B[N];

int W[N];

int bad = 0;

int getbad(int i) {
    return (W[2 * i] > 0 && W[2 * i + 1] > 0) ? 1 : 0;
}

void add(int i, int w) {
    bad -= getbad(i / 2);
    W[i] += w;
    bad += getbad(i / 2);
}

struct ev {
    int t;
    int i;
    int d;
    friend bool operator <(const ev& a, const ev& b) {
        return a.t < b.t;
    }
};

vector<ev> evts;

const int INF = 2e9 + 42;

void add(int l, int r, int i) {
    evts.emplace_back(ev{l, i, 1});
    evts.emplace_back(ev{r + 1, i, -1});
}

int A[N];

void die() {
    puts("-1");
    exit(0);
}

int T(int x) {
    return 2 * x + 1;
}

int F(int x) {
    return 2 * x;
}

int main() {
    int n;
    scanf("%d", &n);
    for (int i = 0; i < n; i++) {
        scanf("%d", &A[i]);
    }

    for (int i = 0; i < n; i++) {
        add(0, A[i] - 1, F(i));
    }
    bool f = false;
    for (int i = 0; i < n - 1; i++) {
        int a = A[i];
        int b = A[i + 1];
        int s = a + b;
        if (a == b) {
            add(0, s, F(i + 1));
            add(0, s, T(i));
            add(s, INF, F(i));
            add(s, INF, T(i + 1));
        } else if (a > b) {
            add(0, s, T(i));
            add(s, INF, T(i + 1));
        } else {
            add(0, s, F(i + 1));
            add(s, INF, F(i));
        }
    }

    add(0, -1, 0); // touch

    sort(evts.begin(), evts.end());

    int goodk = -1;

    for (int l = 0, r = 0; l < (int)evts.size(); l = r) {
        if (evts[l].t >= INF - 2) {
            break;
        }
        while (r < (int)evts.size() && evts[r].t == evts[l].t) {
            r++;
        }
        for (int i = l; i < r; i++) {
            add(evts[i].i, evts[i].d);
        }
        if (bad == 0) {
            goodk = evts[l].t;
            break;
        }
    }
    printf("%d\n", goodk);
    if (goodk != -1) {
        assert(W[2 * n] == 0 || W[2 * n + 1] == 0);
        for (int i = 0; i < n; i++) {
            assert(W[2 * i] == 0 || W[2 * i + 1] == 0);
            printf("%d ", (B[i] = ((W[2 * i] > 0) ? A[i] : goodk - A[i])));
        }
        printf("\n");
        for (int i = 0; i < n - 1; i++) {
            assert(B[i] < B[i + 1]);
        }
        for (int i = 0; i < n; i++) {
            assert(B[i] >= 0);
        }
    }
}

Yet Another Binary Matrix

There may be some exponential time solutions, which is why bounds are set a bit low, but you can also solve this in polynomial time with the matroid intersection algorithm in O(n^4). It might also be possible to solve this with some hill climbing algorithms, the idea is to try to maximize rank(W(A, B + X)) + rank(W(R - A, C - B - X)). I'll describe the matroid intersection algorithm.

The matroids here in this case are M₁ = set of columns X such W(A, X) is linearly independent, and M₂ = set of columns Y such that the rank of W(R - A, C - Y) is at least |R| - |A| (here, the rank is the maximum size of a subset of rows that is linearly independent).

The algorithm is similar to bipartite matching (in fact, bipartite matching is a special case of the matroid intersection algorithm). The rough steps are as follows. Let S be some set of elements that is in $\text{[math]}$ . Initially S is empty. To increase the size of S, make a directed graph as follows:

Make a node for every column in the graph. Also make a node for a "source" and a "sink".
For simplicity, I'll refer to a node not in S as x and a node in S as y.
For two nodes x, y, draw a directed edge from x to y if S + x - y belongs in M₁.
For two nodes x, y, draw a directed edge from x to y if S + x - y belongs in M₂.
Connect the source to x if S + x belongs in M₁.
Connect x to the sink if S + x belongs in M₂.

We then find an "augmenting" path from the source to the sink, and we can xor this with our original set to get a set with one size larger (i.e. if it was in S remove it, otherwise add it).

The proof isn't too easy though, but you can google some papers about the algorithm for proof/more details (here and here).

Of course, this only deals with the unweighted case, so to add back B into consideration, we can give columns in B weight 1 and other columns with weight 0. We can adapt the algorithm above to find the maximum weight instead, and check it contains all elements of B.

code

import java.io.OutputStream;
import java.io.IOException;
import java.io.InputStream;
import java.io.OutputStream;
import java.io.PrintWriter;
import java.util.Arrays;
import java.io.BufferedWriter;
import java.util.InputMismatchException;
import java.io.IOException;
import java.util.TreeSet;
import java.util.ArrayList;
import java.util.List;
import java.util.stream.Stream;
import java.io.Writer;
import java.io.OutputStreamWriter;
import java.util.Comparator;
import java.io.InputStream;

/**
 * Built using CHelper plug-in
 * Actual solution is at the top
 */
public class Main {
    public static void main(String[] args) {
        InputStream inputStream = System.in;
        OutputStream outputStream = System.out;
        InputReader in = new InputReader(inputStream);
        OutputWriter out = new OutputWriter(outputStream);
        YetAnotherBinaryMatrix solver = new YetAnotherBinaryMatrix();
        solver.solve(1, in, out);
        out.close();
    }

    static class YetAnotherBinaryMatrix {
        int n;
        int na;
        int nb;
        int[][] mat;
        int[] a;
        int[] b;
        long[] A;
        long[] nA;
        boolean[] ba;
        boolean[] bb;

        public void solve(int testNumber, InputReader in, OutputWriter out) {
            n = in.nextInt();
            na = in.nextInt();
            nb = in.nextInt();
            a = in.readIntArray(na);
            b = in.readIntArray(nb);
            ba = new boolean[n];
            for (int x : a) ba[x - 1] = true;
            bb = new boolean[n];
            for (int x : b) bb[x - 1] = true;
            mat = new int[n][n];
            for (int i = 0; i < n; i++) {
                char[] c = in.next().toCharArray();
                for (int j = 0; j < n; j++)
                    mat[i][j] = c[j] - '0';
            }
            A = new long[n];
            nA = new long[n];
            for (int i = 0; i < n; i++) {
                for (int j = 0; j < n; j++) {
                    if (ba[j]) A[i] = A[i] * 2 + mat[j][i];
                    else nA[i] = nA[i] * 2 + mat[j][i];
                }
            }
            Basis bs = new Basis();
            for (int i = 0; i < n; i++) bs.add(nA[i]);
            if (bs.size < n - na) {
                out.println(-1);
                return;
            }
            boolean[] ss = new boolean[n];
            while (true) {
                int[] x = findPath(ss);
                if (x == null) break;
                for (int j : x) {
                    ss[j] = !ss[j];
                }
            }
            int count = 0;
            for (boolean w : ss) if (w) count++;
            if (count != na) {
                out.println(-1);
                return;
            }
            count = 0;
            for (int i = 0; i < n; i++) {
                if (bb[i] && !ss[i]) {
                    out.println(-1);
                    return;
                } else if (ss[i] && !bb[i]) {
                    count++;
                }
            }

            out.println(count);
            int[] ret = new int[count];
            int idx = 0;
            for (int i = 0; i < n; i++) if (ss[i] && !bb[i]) ret[idx++] = i + 1;
            out.println(ret);
        }

        public boolean ok1(boolean[] ss) {
            Basis bs = new Basis();
            for (int j = 0; j < n; j++) {
                if (ss[j]) {
                    if (!bs.add(A[j]))
                        return false;
                }
            }
            return true;
        }

        public boolean ok2(boolean[] ss) {
            Basis bs = new Basis();
            for (int j = 0; j < n; j++) {
                if (!ss[j]) {
                    bs.add(nA[j]);
                }
            }
            return bs.size >= n - na;
        }

        public int[] findPath(boolean[] ss) {
            int nnodes = n + 2;
            List<Integer>[] graph = Stream.generate(ArrayList::new).limit(nnodes).toArray(List[]::new);
            for (int i = 0; i < n; i++) {
                for (int j = 0; j < n; j++) {
                    if (!ss[i] && ss[j]) {
                        ss[i] = true;
                        ss[j] = false;
                        if (ok1(ss)) graph[i].add(j);
                        if (ok2(ss)) graph[j].add(i);
                        ss[i] = false;
                        ss[j] = true;
                    }
                }
            }

            for (int i = 0; i < n; i++) {
                if (!ss[i]) {
                    ss[i] = true;
                    if (ok2(ss)) graph[nnodes - 1].add(i);
                    if (ok1(ss)) graph[i].add(nnodes - 2);
                    ss[i] = false;
                }
            }


            int[] prev = new int[nnodes];
            int[] dist = new int[nnodes];
            Arrays.fill(prev, -1);
            Arrays.fill(dist, 1 << 25);
            TreeSet<Integer> ts = new TreeSet<>(Comparator.comparingInt(x -> dist[x] * (n + 10) + x));
            dist[nnodes - 1] = 0;
            ts.add(nnodes - 1);
            while (ts.size() > 0) {
                int f = ts.pollFirst();
                for (int nxt : graph[f]) {
                    int weight = (nxt < n ? 100 * (bb[nxt] ? -1 : 1) * (ss[nxt] ? -1 : 1) : 0) + 1;
                    if (dist[f] + weight < dist[nxt]) {
                        ts.remove(nxt);
                        dist[nxt] = dist[f] + weight;
                        prev[nxt] = f;
                        ts.add(nxt);
                    }
                }
            }
            if (prev[nnodes - 2] == -1) return null;
            int[] p = new int[nnodes];
            int cur = prev[nnodes - 2];
            int id = 0;
            do {
                p[id++] = cur;
                cur = prev[cur];
            } while (cur != nnodes - 1);

            return Arrays.copyOf(p, id);
        }

    }

    static class InputReader {
        private InputStream stream;
        private byte[] buf = new byte[1 << 16];
        private int curChar;
        private int numChars;

        public InputReader(InputStream stream) {
            this.stream = stream;
        }

        public int[] readIntArray(int tokens) {
            int[] ret = new int[tokens];
            for (int i = 0; i < tokens; i++) {
                ret[i] = nextInt();
            }
            return ret;
        }

        public int read() {
            if (this.numChars == -1) {
                throw new InputMismatchException();
            } else {
                if (this.curChar >= this.numChars) {
                    this.curChar = 0;

                    try {
                        this.numChars = this.stream.read(this.buf);
                    } catch (IOException var2) {
                        throw new InputMismatchException();
                    }

                    if (this.numChars <= 0) {
                        return -1;
                    }
                }

                return this.buf[this.curChar++];
            }
        }

        public int nextInt() {
            int c;
            for (c = this.read(); isSpaceChar(c); c = this.read()) {
                ;
            }

            byte sgn = 1;
            if (c == 45) {
                sgn = -1;
                c = this.read();
            }

            int res = 0;

            while (c >= 48 && c <= 57) {
                res *= 10;
                res += c - 48;
                c = this.read();
                if (isSpaceChar(c)) {
                    return res * sgn;
                }
            }

            throw new InputMismatchException();
        }

        public String next() {
            int c;
            while (isSpaceChar(c = this.read())) {
                ;
            }

            StringBuilder result = new StringBuilder();
            result.appendCodePoint(c);

            while (!isSpaceChar(c = this.read())) {
                result.appendCodePoint(c);
            }

            return result.toString();
        }

        public static boolean isSpaceChar(int c) {
            return c == 32 || c == 10 || c == 13 || c == 9 || c == -1;
        }

    }

    static class OutputWriter {
        private final PrintWriter writer;

        public OutputWriter(OutputStream outputStream) {
            writer = new PrintWriter(new BufferedWriter(new OutputStreamWriter(outputStream)));
        }

        public OutputWriter(Writer writer) {
            this.writer = new PrintWriter(writer);
        }

        public void print(int[] array) {
            for (int i = 0; i < array.length; i++) {
                if (i != 0) {
                    writer.print(' ');
                }
                writer.print(array[i]);
            }
        }

        public void println(int[] array) {
            print(array);
            writer.println();
        }

        public void close() {
            writer.close();
        }

        public void println(int i) {
            writer.println(i);
        }

    }

    static class Basis {
        public int size;
        public long[] basis;

        public Basis() {
            basis = new long[100];
            size = 0;
        }

        public boolean add(long x) {
            for (int i = size - 1; i >= 0; i--) {
                x = Math.min(x, x ^ basis[i]);
            }
            if (x == 0) return false;
            basis[size++] = x;
            for (int i = size - 2; i >= 0; i--) {
                if (basis[i] > basis[i + 1]) {
                    long t = basis[i + 1];
                    basis[i + 1] = basis[i];
                    basis[i] = t;
                }
            }
            return true;
        }

    }
}

Comments (18)

Write comment?

the_art_of_war

7 years ago, # |

+13

When opened the author's solution for C and got that v_i can be zero :(

→ Reply

bmerry

For problem C it seems that an O(nk) solution works. I didn't submit it during the contest because I assumed it would be too slow, but I submitted it after the contest (mostly to check that I'd gotten the corner cases right before trying a smarter version) and it passed.

dragoon

7 years ago, # ^ |

And on the other part of the world, there was me, who got TLE on O(nk) solution.

Did you have any mods in your inner loop? My inner loop avoided them.

← Rev. 2 →

Yes. I have a modinv inside outer loop. May be avoiding that would have done the trick.

https://pastebin.com/QXp88ZeK

Xellos

+18

This part of your code

    for (int i = 1; i <= k; i++) {
        int u = s[i];
        for (int v : V[u]) {
            G[v].push_back(cnt[v]);
        }
        cnt[u]++;
    }

is like saying "I can't decide if I want to get TLE or MLE, but I'll make sure to get at least one of them". If the input is a star, you're doing O(KN) push_backs...

Here's my code that runs in just over 1s. The O(nk) part is simply adding v[x] for all neighbours of a vertex in a 64-bit accumulator, so it has low constant factor — but still ought to have timed out given the right test case.

https://pastebin.com/WnMphk9Q

C: I thought O(n * sqrt(n) * log(n)) is not intended to pass.

It can be solved in O(N * sqrt(N) + k ) , where N = n + m.

My solution:

I calculated the value of vertex just before it divided by two. Then sum up all the values after first phase. Calculate the second time the same value but for the second phase and then multiplies it by constant. To get N * sqrt(N) solution, just need to split vertices in big and small by amount of edges.

Code, but code-style is bad

Eryx

Agreed, it looks like it should not pass. Actually my O(n * sqrt(n) * log(n)) solution passes in 2.433 s. I think the constraints have been set a bit too high.

chemthan

I think it is trivial to reduce to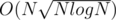 $\text{[math]}$ .

pllk

+35

In D, also a simple greedy way to check a substring worked: repeatedly find a place where you can put a stamp and cover some new characters, and see if you can cover the whole string. This is O(n^5) but only took about 200 ms on the server; I don't know if we could find a test to break it.

Errichto

← Rev. 4 →

+28

C in O(n^1.5)

Let's call a vertex heavy if its degree is at least sqrt(n). Otherwise, it's light.

For every vertex, we linearly compute the initial sum of values of its light neighbors. Then we process changes. When we change a light vertex, we iterate over its neighbors and change their "sums of values of light neighbours". When we change a heavy vertex we just update its own value. When we answer a query, we know "sum of values of light neighbours", and we must additionally iterate over heavy neighbours. It's fast because there are at most O(sqrt(n)) heavy vertices in the graph.

(in fact, we should change n to m in some formulas above, whatever)

quite simple code: https://pastebin.com/aLuidVN4

pleasant

This idea is very succinctly described here by Burunduk1 (Problem 1)

Morphy

another variant: heavy is when the node appears more than sqrt(k) times in the sequence

code: https://pastebin.ubuntu.com/p/nHqSydZZhQ/

+26

D in O(N³):

Let's try all k. For one k, let's look at all substrings with this length, group them by identity (using hashing) and look at each group.

If we're covering with a substring (stamp) w and it occurs at indices id₁ through id_n, we should find for each index id_j the maximum length of a substring [l, r) surrounding it which can be constructed in the following way:

start with [l, r) = [id_j, id_j + k)
while there is a prefix of w which covers [l - d, r) (d is the length of this prefix), extend l to l - d
the same for a suffix of w which covers [l, r + d), extending r to r + d

Each substring [l, r) can obviously be covered with w. If there is a substring u of S that doesn't occur in either of those substrings, two situations can occur:

u is a prefix or suffix of S — there's no way to cover S with w
u is between two substrings [l, r) — iff u is a substring of w, then it's possible to cover S with w

Why? The situations where it's possible to cover S are clear. Otherwise, let's look at the last application of the stamp which covered some character in u. In this operation, we couldn't have covered a proper prefix or proper suffix of u, since that would mean we could either extend one of the strings [l, r) or (when u is a prefix/suffix of S) this prefix/suffix is also a prefix/suffix of S and we'd have one more index among id_1..n. We couldn't have covered an inner substring of u, since we'd also have one more index among id_1..n. The only remaining possibility is that u is fully covered in this one operation, which corresponds to it being an inner substring of w. (Which isn't an option if u is a prefix/suffix of S.)

The above process can be simulated quickly if we precompute the LCP of each pair of suffixes of S (straightforward, O(N³)). There are only O(N²) indices id in total. For each of them, we can keep extending the string by trying all possible values of d until we find one that fits (each can be checked in O(1) using the precomputed LCPs), where we stop and try again. This way, we spend O(N) steps on failing to extend or x steps on extending by x, and we can only extend by O(N) in total. Checking if u is a substring of w can also be done in O(N) by iterating over all suffixes of w and using precomputed LCPs. This way, we take O(N) time per each id.

zemen

I came up with the same solution but with hashes instead of LCP's. I think(but not sure) it can be modified to O(N²). For each fixed l we can precompute maximum prefix at which substring can be extended for each r simultaneously in linear time. The rest part of the solution remains the same.

xuanquang1999

Can anyone elaborate the line sweep that will "find some point such that this point is not in F(i) or not in T(i) for all i" in problem E?

+10

My solution for E:

It's clear that the flipped subsequence has to be decreasing and the non-flipped subsequence increasing. Some prefix of the flipped substring will then consist of elements that decreased when flipped (K - x < x) and the remaining suffix will consist of elements that increased when flipped.

Let's look at any prefix 1..p (possibly empty, the following is irrelevant for p < 2) containing no elements that increased. This prefix follows a simple rule: if x_p - 1 < x_p, then x_p - 1 shouldn't be flipped; otherwise it should. (The latter holds since x_p can't be any smaller; the former because element p is either non-flipped, where x_p - 1 should be greedily maximised, or because it is flipped, in which case flipping x_p - 1 wouldn't make the final sequence increasing.)

For each prefix and each state of its last element, we can now compute an interval of valid K in case it doesn't contain increased elements — we already know the states (flipped/non-flipped) of all previous elements, so this is straightforward O(N) DP.

A similar DP can be done for each suffix in case it doesn't contain decreased elements. Now we can check all cases "prefix 1..i is of the first type, suffix i + 1..N of the second type", try all (up to 4) options for the states of the last element of the prefix and the first element of the suffix (if they exist), compute an additional constraint on K, combine this with the intervals of valid K for the prefix and suffix, and if there's some valid K as a result, construct the solution greedily using it.

Also, my solution for B:

Meet in the middle. For each sequence of 5 numbers, compute the shortest prefix and longest suffix containing it, then check for each sequence in O(1) if it can be constructed. Time complexity O(10·9·8·7·6·|S| + 10!).

Lewin's blog