Let's discuss problems.
How to solve the geography problem?
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 158 |
| 5 | atcoder_official | 157 |
| 6 | Qingyu | 156 |
| 7 | djm03178 | 151 |
| 7 | adamant | 151 |
| 9 | luogu_official | 150 |
| 10 | awoo | 147 |
Let's discuss problems.
How to solve the geography problem?
Hey guys! Hello IOI 2018 contestants. How's everything at Japan?
Let's use this thread to get updates and discuss problems. Day 1 contest is a few hours away. Anyone who has a mirror link / live ranklist link please post in comments.
Hope everyone has a wonderful time!
We all have been waiting for this, a clean readable text version of Looking for a Challenge! My man Bar-B-Q informed me of it being finally out.
So without further adieu, here goes the link: https://www.nras.org.uk/data/events%20flyer%20front%20and%20back.pdf
Enjoy and leave a thanks for my man Bar-B-Q here. ^_^
Link: https://toph.co/p/breaking-math
The task is simple. Given n, k you gotta print
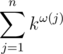
where ω(j) is the number of distinct prime factors of j.
Constraints: 1 ≤ k ≤ 10, 1 ≤ n ≤ 1011.
TL is fuckin' big, 15 seconds. Wut do?
Problem: 351E - Джефф и перестановка
Abridged statement: given n ≤ 2000 integers, we can multiply some of them by - 1. Goal is to minimize number of inversions (pairs (i, j) such that i < j and ai > aj). Print the minimum number of inversions.
Solution: 30244905
This solution replaces all numbers with its absolute value first. Then for each index i this solution adds min(L, R) to answer where L = number of smaller elements to left, R = number of smaller elements to right. Why does it work?
Why don't the IOI committee publish shortlisted problems and solutions like IMO does? It would be a great source of practice and countries could use the problems in their selection tests.
| Name |
|---|


