Hi everybody!
Hope you liked our Revolution of Colors and Titles. Maybe you even have took part in a contest in new status. The last round have set an incredible record: 8000 participants! And I'm glad to tell you that there was no single technical issue during the round time! Consider the 15-minute delay as a part of our evil plan for setting up a new record :)
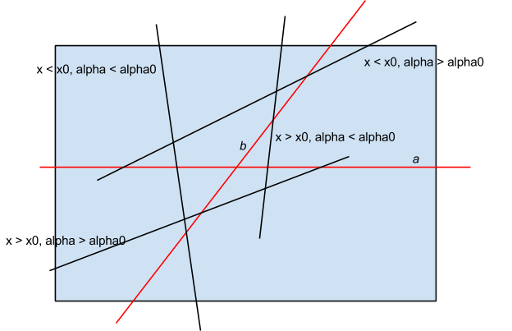
I'm glad to tell that Codeforces team is able not only to tune colors and formulas, but also to work on new features for you. You may see on contests page that there is a list of authors for each of the rounds! Moreover, in profile of a person there is now an entry called "problemsetting" that allows you to see the list of all contests in whose preparation a person took a part.
Endagorion looks like this.









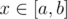 in the tree the function
in the tree the function  runs of gradient calculation we almost solved the problem. Let's understand where exactly the answer is located. Note that the global optimum will most probably be located inside some edge. It is easy to see that the optimum vertex will be one of the vertices incident to that edge, or more specifically, one of the last two considered vertices by our algorithms. Which exactly can be determined by calculating the exact answer for them and choosing the most optimal among them.
runs of gradient calculation we almost solved the problem. Let's understand where exactly the answer is located. Note that the global optimum will most probably be located inside some edge. It is easy to see that the optimum vertex will be one of the vertices incident to that edge, or more specifically, one of the last two considered vertices by our algorithms. Which exactly can be determined by calculating the exact answer for them and choosing the most optimal among them. .
.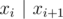 for (
for (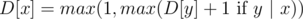 for all
for all 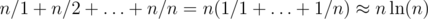 transitions.
transitions.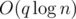 .
. 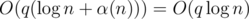 time.
time.




 and get a virtual medal!
and get a virtual medal!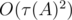 where
where 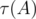 is the number of divisors of
is the number of divisors of 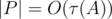 ). So, overall complexity of the solution is
). So, overall complexity of the solution is 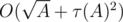 .
.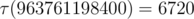 . Nice estimate that is not an exact asymptotic, though, is that
. Nice estimate that is not an exact asymptotic, though, is that 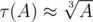 )
)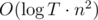 and then to
and then to 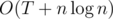


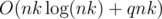 or
or 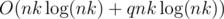 . For each possible value
. For each possible value 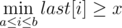 . That means that we can keep the values
. That means that we can keep the values 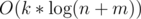 .
.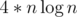 running time. But unfortunately the statement contained wrong constraints, so we reduced input size during the tour. Nevertheless, we will add the harder version of this task and you will be able to submit it shortly.
running time. But unfortunately the statement contained wrong constraints, so we reduced input size during the tour. Nevertheless, we will add the harder version of this task and you will be able to submit it shortly.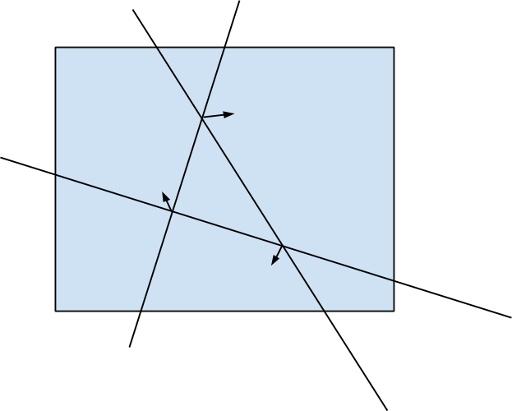
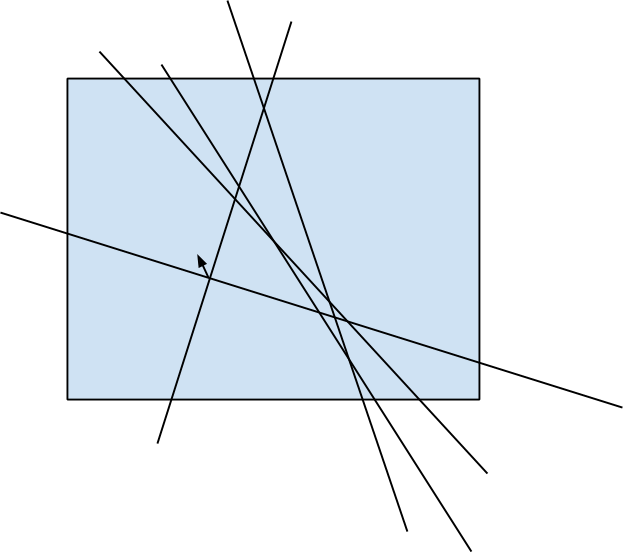
 by fixing the first side of the angle and then adding lines in ascending order of polar angle, and then by keeping the number of lines that intersect the base line to the left and that intersect the base line to the right. Key idea is that the exact of four angles formed by the pair of lines
by fixing the first side of the angle and then adding lines in ascending order of polar angle, and then by keeping the number of lines that intersect the base line to the left and that intersect the base line to the right. Key idea is that the exact of four angles formed by the pair of lines