Thank you for participating in this round! Problems A and G are authored by Cocoly1990 and the rest by me.
Currently, I'm not sure if the editorials are fine enough. Please feel free to tell me where I can improve.
| A | B | C | D | E | F | G | H | I | |
|---|---|---|---|---|---|---|---|---|---|
| _istil | 800 | 1200 | 1400 | 1700 | 1900 | 2500 | [2800, 3300] | 3200 | [800, 3000] |
| Cocoly1990 | 800 | 1300 | 3000 | ||||||
| TheScrasse | 800 | 1200 | ? | 1800 | 2500 | 3000 | 3000 | 3500 | |
| LMydd0225 | 800 | 1300 | 1600 | 1900 | 2100 | 2400 | 2800 | 2900 | [2500, 3200] |
| Error_Yuan | 900 | 1200 | 1400 | 2000 | 2100 | 2500 | 3000 | 3200 | |
| Caylex | 800 | 1300 | 1500 | 1900 | 2200 | 2600 | [2500, 3100] | ||
| tzl_Dedicatus545 | 800 | 1000 | 1100 | 1400 | 2300 | ||||
| PaciukZvichainyi | 800 | 1200 | 1500 | 1800 | 2100 | 2500 | |||
| doujinshi_master | 800 | 1200 | 1500 | 1800 | |||||
| juan_123 | 800 | [800, 1100] | 1000 | 1700 | 2400 | 2800 | [2700, 3500] | ||
| StarSilk | 800 | 1300 | 1400 | 1700 | 2500 | 3100 | 2700 | ||
| SkyWave2022 | 800 | 1200 | 1600 | [1600, 1900] | |||||
| ABitVeryScaredOfWomen | 800 | 1200 | 1500 | 1800 | 2100 | ||||
| FFTotoro | 800 | 1200 | 1400 | 1900 | 1900 | 2400 | 2900 |
Can you find a partition that is always valid?
Suppose you are given a set $$$S$$$. How do you judge whether $$$S$$$ is stable in $$$\mathcal O(\lvert S\rvert)$$$?
Are sets that are very large really necessary?
Note that: we always have a partition like $$$[a_1], [a_2], \dots, [a_n]$$$, since $$$(x, x, x)$$$ always forms a non-degenerate (equilateral) triangle.
We focus on the second partition scheme in which not all continuous subsegments have a length of $$$1$$$. One can also note that if a set $$$S$$$ is stable then for all $$$T \subsetneq S$$$ ($$$T \neq \varnothing$$$), $$$T$$$ is also stable.
- Short proof: If $$$\exists u, v, w \in T$$$ such that $$$(u, v, w)$$$ doesn't form a non-degenerate triangle, therefore $$$u, v, w \in S$$$ so it is concluded that $$$S$$$ is not stable. Contradiction!
If such a partition exists, we can always split long continuous subsegments into shorter parts, while the partition remains valid. Therefore, it's enough to check the case in which there is one subsegment of length $$$2$$$ and the rest of length $$$1$$$. So, we should output NO if and only if for all $$$1 \leq i < n$$$, $$$2\min(a_i, a_{i+1}) \leq \max(a_i, a_{i+1})$$$.
#include <bits/stdc++.h>
#define MAXN 1001
int a[MAXN];
void solve() {
int n; std::cin >> n;
for (int i = 1; i <= n; ++i) std::cin >> a[i];
for (int i = 1; i < n; ++i) if (2 * std::min(a[i], a[i + 1]) > std::max(a[i], a[i + 1]))
{ std::cout << "YES\n"; return; }
std::cout << "NO\n";
}
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr), std::cout.tie(nullptr);
int t; std::cin >> t; while (t--) solve(); return 0;
}
2053B - Outstanding Impressionist
What if for all $$$1 \leq i \leq n$$$, $$$l_i \ne r_i$$$ holds? How do you prove it?
Use prefix sums or similar to optimize your solution.
For each $$$1 \leq i \leq n$$$, for each $$$l_i \leq x \leq r_i$$$, we want to check if it is okay for impression $$$i$$$ being unique at the value of $$$x$$$. Note that: for each $$$j \neq i$$$, we can always switch $$$w_j$$$ to a value different from $$$x$$$ if $$$l_j \neq r_j$$$, since there are at least two options. Therefore, it is impossible if and only if there exists a $$$1 \leq j \leq n$$$ with $$$j \neq i$$$ such that $$$l_j = r_j = x$$$.
Let's record $$$a_i$$$ as the number of different $$$k$$$ satisfying $$$1 \leq k \leq n$$$ and $$$l_k = r_k = i$$$. If $$$l_i \neq r_i$$$, then we say impression $$$i$$$ cannot be made unique if and only if for all $$$l_i \leq k \leq r_i$$$, $$$a_k \geq 1$$$; otherwise ($$$l_i = r_i$$$), it cannot be unique if and only if $$$a_{l_i} \geq 2$$$.
This can all be checked quickly within a prefix sum, so the overall time complexity is $$$\mathcal O(\sum n)$$$.
#include <bits/stdc++.h>
#define MAXN 400001
int l[MAXN], r[MAXN], sum[MAXN], cnt[MAXN];
void solve() {
int n; std::cin >> n;
for (int i = 1; i <= 2 * n; ++i) sum[i] = cnt[i] = 0;
for (int i = 1; i <= n; ++i) {
std::cin >> l[i] >> r[i];
if (l[i] == r[i]) sum[l[i]] = 1, ++cnt[l[i]];
}
for (int i = 2; i <= 2 * n; ++i) sum[i] += sum[i - 1];
for (int i = 1; i <= n; ++i)
std::cout << ((l[i] == r[i] ? cnt[l[i]] <= 1 : sum[r[i]] - sum[l[i] - 1] < r[i] - l[i] + 1) ? "1" : "0");
std::cout << '\n';
}
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr), std::cout.tie(nullptr);
int t; std::cin >> t; while (t--) solve(); return 0;
}
Process many segments simultaneously. What kind of segments do we process at a time?
The length.
The point that must be noted is: that if we call the process of splitting a large segment into two smaller segments a round, then all segments are of the same length when the $$$i$$$-th round of the observation is conducted; and, the number of rounds does not exceed $$$\mathcal O(\log n)$$$. The $$$k$$$ restriction is equivalent to specifying that only a certain prefix of rounds is computed.
Here are some different approaches:
- (Most succinctly) Note that the distribution of segments after round 1 is centrally symmetric; Also, $$$x$$$ and $$$y$$$ being centrally symmetric implies that $$$x + y = n + 1$$$, so it is simple to calculate by simulating the number of segments and the length directly.
- If a segment $$$[l, r]$$$ is split into $$$[l, m - 1]$$$ and $$$[m + 1, r]$$$, its left endpoint sum changes from $$$l$$$ to $$$2l + \frac{r - l}{2} + 1$$$, and since $$$(r - l)$$$ is fixed, the sum of the left endpoints of all segments can be maintained similarly.
- The following recursive method also works: the answer to $$$n$$$ can be recovered by the answer to $$$\lfloor \frac{n}{2} \rfloor$$$. The time complexity is $$$\mathcal O(t\log n)$$$.
This is written by _TernaryTree_.
#include <bits/stdc++.h>
#define int long long
using namespace std;
int T;
int n, k;
signed main() {
cin >> T;
while (T--) {
cin >> n >> k;
int mul = n + 1, sum = 0, cur = 1;
while (n >= k) {
if (n & 1) sum += cur;
n >>= 1;
cur <<= 1;
}
cout << mul * sum / 2 << endl;
}
return 0;
}
2053D - Refined Product Optimality
What if $$$q = 0$$$?
How do you keep the array sorted?
The problem makes no difference when both $$$a$$$ and $$$b$$$ can be rearranged. Let the rearranged arrays of $$$a$$$ and $$$b$$$ be $$$c$$$ and $$$d$$$ respectively.
If $$$q = 0$$$, we can write $$$c$$$ as $$$\operatorname{SORTED}(a_1, a_2 \ldots, a_n)$$$ and $$$d$$$ as $$$\operatorname{SORTED}(b_1, b_2 \ldots, b_n)$$$. It can be proved that this reaches the maximum value: if not so, then
- There must be some pair $$$(i, j)$$$ such that $$$c_i < c_j, d_i > d_j$$$.
- Since $$$\min(c_i, d_i) \cdot \min(c_j, d_j) = c_i \cdot \min(c_j, d_j) \leq c_i \cdot \min(c_j, d_i) = \min(c_i, d_j) \cdot \min(c_j, d_i)$$$, we can swap $$$d_i$$$ and $$$d_j$$$, and the product does not decrease.
Consider the modification, which is a single element increment by $$$1$$$. Without loss of generality, let $$$c_x$$$ be increased by $$$1$$$ (and the processing method for $$$d$$$ is the same). If $$$c_x < c_{x+1}$$$, then after the modification $$$c_x \leq c_{x+1}$$$, which would be fine. Otherwise, we can modify the array $$$c$$$ in the form of a single round of "Insertion Sort": We continuously swap $$$c_x$$$ and $$$c_{x+1}$$$, $$$x \gets x + 1$$$, until $$$c_x < c_{x+1}$$$ (or $$$x = n$$$), and thus the array remains sorted after the increment.
In fact, the swap operation does nothing in the above process: in these cases, $$$c_x = c_{x+1}$$$ holds! So we can just set $$$x'$$$ as the maximum $$$k$$$ such that $$$c_k = c_x$$$, and then increase $$$c_{x'}$$$ by $$$1$$$, after which $$$c$$$ is still sorted. The $$$k$$$ can be found with a naive binary search, so the problem is solved in $$$\mathcal O(n\log n + q(\log p + \log n))$$$ per test case.
#include <bits/stdc++.h>
constexpr int MOD = 998244353;
int qpow(int a, int x = MOD - 2) {
int res = 1;
for (; x; x >>= 1, a = 1ll * a * a % MOD) if (x & 1) res = 1ll * res * a % MOD;
return res;
}
#define MAXN 200001
int a[MAXN], b[MAXN], c[MAXN], d[MAXN];
void solve() {
int n, q, res = 1; std::cin >> n >> q;
for (int i = 1; i <= n; ++i) std::cin >> a[i], c[i] = a[i];
for (int i = 1; i <= n; ++i) std::cin >> b[i], d[i] = b[i];
std::sort(c + 1, c + n + 1), std::sort(d + 1, d + n + 1);
for (int i = 1; i <= n; ++i) res = 1ll * res * std::min(c[i], d[i]) % MOD;
std::cout << res << " \n"[q == 0];
for (int i = 1, op, x; i <= q; ++i) {
std::cin >> op >> x;
if (op == 1) {
int p = std::upper_bound(c + 1, c + n + 1, a[x]) - c - 1;
if (c[p] < d[p]) res = 1ll * res * qpow(c[p]) % MOD * (c[p] + 1) % MOD;
++a[x], ++c[p];
} else {
int p = std::upper_bound(d + 1, d + n + 1, b[x]) - d - 1;
if (d[p] < c[p]) res = 1ll * res * qpow(d[p]) % MOD * (d[p] + 1) % MOD;
++b[x], ++d[p];
}
std::cout << res << " \n"[i == q];
}
}
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr), std::cout.tie(nullptr);
int t; std::cin >> t; while (t--) solve(); return 0;
}
2053E - Resourceful Caterpillar Sequence
Suppose somebody wins. In which round does he or she win?
A player can always undo what his opponent did in the previous turn.
Can you find the necessary and sufficient condition for $$$(p, q)$$$ to be a caterpillar that makes Aron win?
Denote Nora's first move as round $$$1$$$, Aron's first move as round $$$2$$$, and so on. Suppose a player does not have a winning strategy in the $$$k$$$-th round, but he or she has a winning strategy in the $$$(k + 2)$$$-th round — it can be shown impossible because the other player can always withdraw the last move of another player so that the status is the same as it was before the $$$k$$$-th round.
Therefore: if a player wins in the $$$k$$$-th round, we claim that $$$k \leq 2$$$.
Given $$$p, q$$$, let's determine who will eventually win the game.
- If both $$$p$$$ and $$$q$$$ are leaves, the result is a tie.
- If $$$p$$$ is a leaf while $$$q$$$ is not, Nora wins.
- If $$$q$$$ is a leaf while $$$p$$$ is not, Aron wins.
- If neither $$$p$$$ nor $$$q$$$ is a leaf:
- Can $$$k = 1$$$? Nora wins if and only if $$$p$$$ is adjacent to a leaf.
- Can $$$k = 2$$$? Aron wins if and only if $$$p$$$ is not adjacent to a leaf, and $$$f(p, q)$$$ is adjacent to a leaf.
- Otherwise, the result is a tie.
The counting part can also be solved easily in $$$\mathcal O(n)$$$. Denote $$$c$$$ as the number of leaves. The initial answer would be $$$c \cdot (n - c)$$$, considering the third case. For the fourth case, we can enumerate $$$m = f(p, q)$$$, which is adjacent to at least one leaf. Given $$$m$$$, $$$q$$$ must be a non-leaf neighbor of $$$m$$$, and let the number of different $$$q$$$ be $$$k$$$. For each of the potential $$$p$$$, which is a non-leaf node whose neighbors are all non-leaf nodes too, it is computed exactly $$$k - 1$$$ times for all the $$$k$$$ candidates of $$$q$$$ (since $$$m$$$ must be on the simple path from $$$p$$$ to $$$q$$$), so the extra contributions are easy to calculate. (If you do not think that much, you can use some simple DP, which I will not elaborate here.)
#include <bits/stdc++.h>
#define MAXN 200001
std::vector<int> g[MAXN];
inline int deg(int u) { return g[u].size(); }
int d[MAXN];
void solve() {
int n; std::cin >> n; long long ans = 0;
for (int i = 1, u, v; i < n; ++i) {
std::cin >> u >> v;
g[u].push_back(v), g[v].push_back(u);
}
int c1 = 0, c2 = 0;
for (int i = 1; i <= n; ++i) c1 += (deg(i) == 1);
ans += 1ll * c1 * (n - c1);
for (int i = 1; i <= n; ++i) if (deg(i) > 1) {
for (int v : g[i]) d[i] += (deg(v) > 1);
c2 += (d[i] == deg(i));
}
for (int m = 1; m <= n; ++m) if (deg(m) > 1 && d[m] != deg(m))
ans += 1ll * c2 * (d[m] - 1);
std::cout << ans << '\n';
for (int i = 1; i <= n; ++i)
(std::vector<int>()).swap(g[i]), d[i] = 0;
}
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr), std::cout.tie(nullptr);
int t; std::cin >> t; while (t--) solve(); return 0;
}
2053F - Earnest Matrix Complement
Special thanks to LMydd0225 for implementing a correct MCS ahead of me, and Error_Yuan for generating the test data for this problem.
What are we going to fill into the matrix? In other words, is there any relationship between the filed numbers?
Try to come up with a naive DP solution that works in large time complexity, such as $$$\mathcal O(nk^2)$$$.
For many different numbers between two consecutive rows, however, the transition is almost the same.
If $$$x' = \max(a, x + b)$$$ and $$$x'' = \max(c, x' + d)$$$, then $$$x'' = \max(\max(a + d, c), x + b + d)$$$.
Conclusion: For each row, an optimal solution exists, such that the newly filled-in numbers are the same.
- Proof: Consider fixing the rows $$$i - 1$$$ and $$$i + 1$$$, and observe all the newly filled-in numbers at row $$$i$$$. Then a new number $$$u$$$ brings a contribution of $$$c_{u, i-1} + c_{u, i+1}$$$, and it is clear that there exists a scheme that takes the maximum value such that all the $$$u$$$ filled in are equal. Adjusting for each row leads to the above conclusion.
Consider dp. Let $$$f_{i,j}$$$ denote the maximum contribution that can be achieved between the first $$$i$$$ rows (ignoring the initial contribution) when the empty elements in the $$$i$$$-th row are filled with $$$j$$$. Let $$$c_i$$$ be the number of $$$-1$$$ numbers in the $$$i$$$-th row, and $$$d_{i,j}$$$ denote the number of elements $$$j$$$ in the $$$i$$$-th row initially.
The transfer should be as follows:
In addition to being able to optimize the above transition to $$$\mathcal O(nk)$$$, the present problem in a matrix has a good property. Specifically, for the same $$$i$$$, there are only $$$\mathcal O(m)$$$ values of $$$j$$$ such that $$$d_{i,j} \neq 0$$$!
If $$$d_{i,j} = 0$$$ and $$$d_{i-1, j} = 0$$$, the original transfer can be viewed as
This can be seen as a global modification in the form of $$$x \gets \max(a, x + b)$$$. The tags are composable in $$$\mathcal O(1)$$$; Otherwise, we can brutely update the new $$$dp_j$$$ for $$$\mathcal O(m)$$$ positions.
Therefore, this problem is solved in $$$\mathcal O(nm)$$$. We decided to let every segment tree solution pass comfortably, so that we set small constraints and large TL.
Bonus Hint for implementation: always use $$$\max(a, dp_j + b)$$$ to get the real value.
#include <bits/stdc++.h>
namespace FastIO {
char buf[1 << 21], *p1 = buf, *p2 = buf;
#define getchar() (p1 == p2 && (p1 = buf, p2 = (p1 + fread(buf, 1, 1 << 21, stdin))) == p1 ? EOF : *p1++)
template <typename T> inline T read() { T x = 0, w = 0; char ch = getchar(); while (ch < '0' || ch > '9') w |= (ch == '-'), ch = getchar(); while ('0' <= ch && ch <= '9') x = x * 10 + (ch ^ '0'), ch = getchar(); return w ? -x : x; }
template <typename T> inline void write(T x) { if (!x) return; write<T>(x / 10), putchar((x % 10) ^ '0'); }
template <typename T> inline void print(T x) { if (x > 0) write<T>(x); else if (x < 0) putchar('-'), write<T>(-x); else putchar('0'); }
template <typename T> inline void print(T x, char en) { print<T>(x), putchar(en); }
#undef getchar
}; using namespace FastIO;
using ll = long long;
void solve() {
int n = read<int>(), m = read<int>(), k = read<int>(); ll cntP = 0, cntQ = 0;
std::vector<int> vep(m), veq(m), cntp(k + 1), cntq(k + 1), vis(k + 1);
std::vector<ll> dp(k + 1); ll a = 0, b = 0, v = 0, ext = 0; // max(a, x + b).
cntp[0] = cntq[0] = m;
auto get = [&](int x) -> int { return (~x) ? x : 0; };
auto read_q = [&]() -> void {
for (int i = 0; i < m; ++i) --cntq[get(veq[i])];
for (int i = 0; i < m; ++i) ++cntq[get(veq[i] = read<int>())];
cntQ = cntq[0];
};
auto roll = [&]() -> void { std::swap(vep, veq), std::swap(cntp, cntq), std::swap(cntP, cntQ); };
auto chkmax = [&](ll &a, ll b) -> void { a = std::max(a, b); };
read_q(), roll();
for (int i = 2; i <= n; ++i) {
read_q();
ll max_dp = std::max(a, v + b);
for (int k : vep) if (~k) chkmax(max_dp, std::max(a, dp[k] + b) + cntP * cntq[k]);
for (int k : veq) if (~k) chkmax(max_dp, std::max(a, dp[k] + b) + cntP * cntq[k]);
for (int k : vep) if ((~k) && vis[k] != i) {
vis[k] = i, ext += 1ll * cntp[k] * cntq[k];
dp[k] = std::max(a, dp[k] + b) + cntP * cntq[k] + cntQ * cntp[k] - b;
chkmax(dp[k], max_dp + cntp[k] * cntQ - b - cntP * cntQ);
chkmax(v, dp[k]);
} for (int k : veq) if ((~k) && vis[k] != i) {
vis[k] = i;
dp[k] = std::max(a, dp[k] + b) + cntP * cntq[k] + cntQ * cntp[k] - b;
chkmax(dp[k], max_dp + cntp[k] * cntQ - b - cntP * cntQ);
chkmax(v, dp[k]);
} a = std::max(max_dp, a + cntP * cntQ), b += cntP * cntQ;
roll();
} print<ll>(std::max(a, v + b) + ext, '\n');
}
int main() { int T = read<int>(); while (T--) solve(); return 0; }
Special thanks to LMydd0225 for generating the test data for this problem, and TheScrasse for providing an alternative solution.
And thanks to Caylex for implementing a really correct MCS and rewriting the editorial, and crazy_sea for offering a suggestion.
(If we do not have to be deterministic) We do not need any hard string algorithm.
In what cases won't greed work? Why?
Is your brute forces actually faster (maybe you can explain it by harmonic series)?
Let's call the prefix $$$s_1$$$ the short string and the suffix $$$s_2$$$ the long string. If $$$\lvert s_1\rvert\gt \lvert s_2\rvert$$$, swapping the order doesn't affect the answer.
Consider a greedy approach. We first match a few short strings until we can't match anymore. If we can't match, we try discarding a few short strings and placing one long string. We enumerate how many short strings to discard. Find the first position where we can place a long string. We call this placing once a "matching process." The starting position of each "matching process" is the next position after the previous "matching process."
However, this approach has a flaw. Below, I will explain the situation where this flaw occurs.
It's not difficult to view the long string as several short strings concatenated with a "tail" at the end.
Why only find the first position? Why wouldn't it be better to backtrack and discard a few more $$$s_1$$$'s before placing the long string?
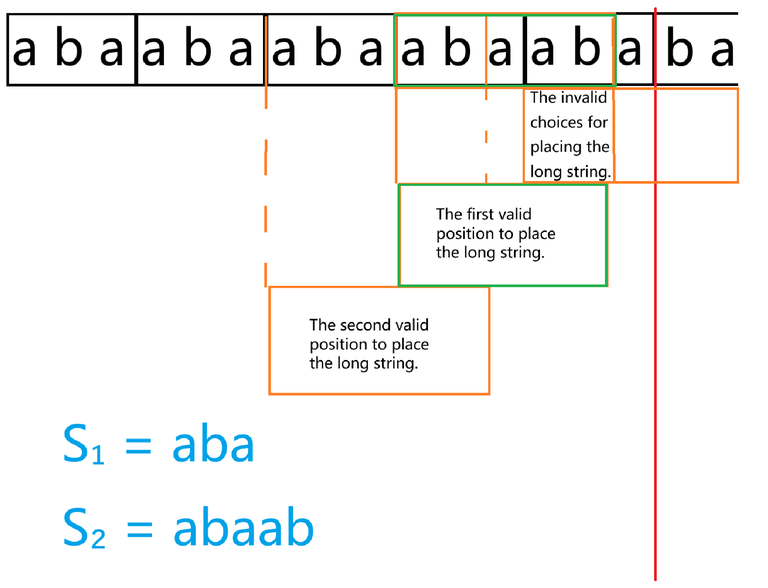
The diagram above is an example. The red line indicates the cutoff position for matching $$$s_1$$$. The three orange boxes represent the possible choices for attempting to match the long string.
The last one is invalid, so skip it. Replace it with the "The first valid position to place the long string." box. This box is correct.
The difference between choosing the second box and the first box is that when we end the matching and proceed to the next round, the content we need to match is that a suffix of $$$s_1$$$ has been moved to the beginning of $s_1$。
As shown in the diagram.
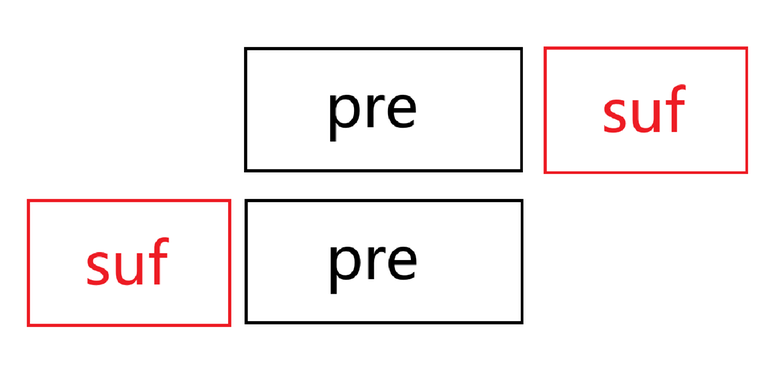
The alignment results in the following diagram.
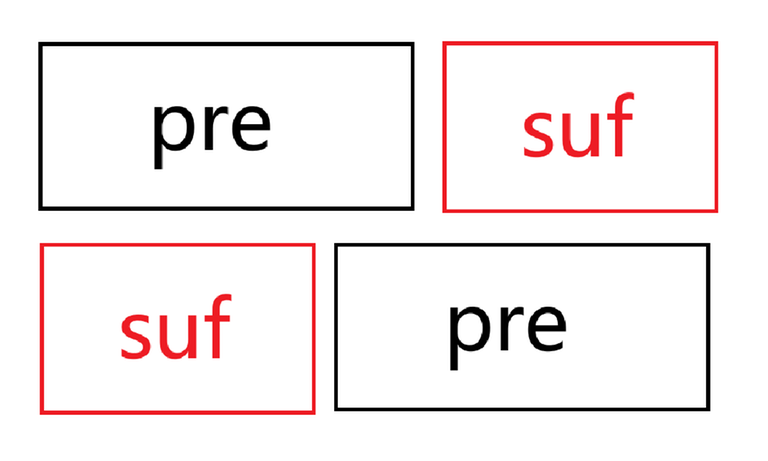
In the diagram, the case where $$$\lvert pre\rvert \gt \lvert suf\rvert$$$ is shown. The other case follows similarly.
$$$pre+suf=suf+pre$$$, and as can be seen from the diagram, here $$$pre+suf$$$ needs to be "misaligned but equal." This means that $$$s_1$$$ must have a periodic cycle, and the "tail" must also be able to be formed through this cycle. Additionally, the $$$\lvert s_1 \rvert$$$ characters at the beginning of $$$s_2$$$ must still be able to be formed by the periodic cycle.
In summary, it is equivalent to $$$s_1$$$ and $$$s_2$$$ having a common periodic cycle.
In other words, backtracking twice can lead to a solution, but backtracking once may not always work. It is necessary for $$$s_1$$$ and $$$s_2$$$ to have a common periodic cycle.
Having a common periodic cycle is too specific. First, the common periodic cycle of these two strings must indeed be the periodic cycle of string $$$s$$$. By finding this cycle in advance, it essentially becomes a problem of solving an equation. Let $$$a=\lvert s_1\rvert $$$ and $$$b=\lvert s_2\rvert$$$, and we need to check whether there are non-negative integer solutions $$$x$$$ and $$$y$$$ that satisfy the equation $$$xa+yb=\lvert s \rvert$$$.
This equation-solving part is just for show. We enumerate $$$y$$$, and for each value of $$$y$$$, we compute the enumeration $$$\mathcal O\left(\frac{m}{n}\right)$$$ times. At most, we do this $$$n$$$ times, so the overall complexity is $$$\mathcal O(m)$$$.
If we directly implement this, the worst-case complexity is related to the harmonic series. Consider a case like $$$s_1 = \texttt{a}, s_2 = \texttt{aaaaaaaab}$$$, and $$$t = \texttt{aaaaaaaaaaaaaaaaaaaaaaaaab}$$$. In this case, we would need to attempt $$$\mathcal O\left(\frac{m}{\lvert s_1\rvert }\right)$$$ steps to finish matching the short string. Each time we backtrack, it requires at most $$$\mathcal O\left(\frac{m}{\lvert s_2\rvert }\right)$$$ steps, and each of those takes $$$\mathcal O\left(\frac{\lvert s_2\rvert }{\lvert s_1\rvert }\right)$$$.
Thanks to orzdevinwang and crazy_sea for pointing out it!
Yes, this problem can indeed be solved in linear time.
First, let the prefix of the long string contain $$$c$$$ short strings. Then, the first "valid position to place the long string" we backtrack to can only be obtained by either backtracking $$$c$$$ short strings or $$$c+1$$$ short strings.
This is easy to understand. Backtracking $$$c$$$ short strings means considering the prefix of the long string, then adding the "tail" of the long string. Backtracking $$$c + 1$$$ short strings only happens when the "tail" part of the long string is a prefix of the short string. For example, the hack in the CF comment section:
https://codeforces.net/blog/entry/136455?#comment-1234262
1
8 8
abaabaab
abaababa
The correct output should be:
0010000
When $$$k = 3$$$, $$$s_1 = \texttt{aba}$$$, $$$s_2 = \texttt{abaab}$$$, we first filled in 2 short strings, but if we backtrack $$$c = 1$$$ short string, it will be judged as unsolvable. This is how the error in std occurs. This situation only arises when the "tail" part of $$$s_2$$$ is a prefix of $$$s_1$$$.
So, each time we calculate, we first use binary search to find this $$$c$$$, and the complexity is $$$\mathcal O\left(\sum\limits_{i=1}^n\log(\frac n i)\right)=\mathcal O(n)$$$. After that, backtracking only requires two checks. The backtracking process becomes linear.
Next, let's accelerate the process of filling in short strings. The hack for brute-force filling has already been given above. If we directly use the method that everyone initially thought was correct, which is the "binary search for the number of short string occurrences" method, Then it can be accelerated by this set of hacks to achieve a $$$\log$$$ complexity.
1
2 5000000
ab
abababab....abababab
crazy_sea points out an alternative solution.
Similar to block division, let $$$B = \frac{n}{\lvert s_1\rvert}$$$. We first try to match $$$B$$$ occurrences of $$$s_1$$$, meaning that each match can move forward by $$$n$$$ positions. After that, the remaining part will not exceed $$$B$$$ occurrences, and we binary search to find how many are left. For the part where we moved forward by $$$B$$$ occurrences, we can backtrack at most once, and then the binary search will take $$$\mathcal O(\log B)$$$. Each time, we can at least fill in $$$\lvert s_2\rvert $$$ occurrences. The time complexity for calculating the answer becomes $$$\mathcal O\left(\frac{m}{\lvert s_2\rvert }\log B\right)$$$, and the total complexity, due to $$$\mathcal O\left(\sum\limits_{i=1}^n \log(\frac{n}{i})\right) = \mathcal O(n)$$$, is $$$\mathcal O(m)$$$.
Thus, the problem is solved in linear time.
During testing, we found that jqdai0815's solution is actually more violent than we thought (We have also received something similar in contest).
He specially handled the case in which $$$X$$$ and $$$T$$$ share a common shortest period, and for the rest $$$i$$$, he just used two queues to optimize the BFS progress (actually changing it to std::priority_queue<int> or similar also works), and it passed just seeming to have a larger constant time complexity.
I'm curious if anybody can (hack it or) prove that it is correct. Thanks in advance!
This is written by Caylex.
#include <bits/stdc++.h>
using namespace std;
template <int P>
class mod_int
{
using Z = mod_int;
private:
static int mo(int x) { return x < 0 ? x + P : x; }
public:
int x;
int val() const { return x; }
mod_int() : x(0) {}
template <class T>
mod_int(const T &x_) : x(x_ >= 0 && x_ < P ? static_cast<int>(x_) : mo(static_cast<int>(x_ % P))) {}
bool operator==(const Z &rhs) const { return x == rhs.x; }
bool operator!=(const Z &rhs) const { return x != rhs.x; }
Z operator-() const { return Z(x ? P - x : 0); }
Z pow(long long k) const
{
Z res = 1, t = *this;
while (k)
{
if (k & 1)
res *= t;
if (k >>= 1)
t *= t;
}
return res;
}
Z &operator++()
{
x < P - 1 ? ++x : x = 0;
return *this;
}
Z &operator--()
{
x ? --x : x = P - 1;
return *this;
}
Z operator++(int)
{
Z ret = x;
x < P - 1 ? ++x : x = 0;
return ret;
}
Z operator--(int)
{
Z ret = x;
x ? --x : x = P - 1;
return ret;
}
Z inv() const { return pow(P - 2); }
Z &operator+=(const Z &rhs)
{
(x += rhs.x) >= P && (x -= P);
return *this;
}
Z &operator-=(const Z &rhs)
{
(x -= rhs.x) < 0 && (x += P);
return *this;
}
Z operator-() { return -x; }
Z &operator*=(const Z &rhs)
{
x = 1ULL * x * rhs.x % P;
return *this;
}
Z &operator/=(const Z &rhs) { return *this *= rhs.inv(); }
#define setO(T, o) \
friend T operator o(const Z &lhs, const Z &rhs) \
{ \
Z res = lhs; \
return res o## = rhs; \
}
setO(Z, +) setO(Z, -) setO(Z, *) setO(Z, /)
#undef setO
friend istream &
operator>>(istream &is, mod_int &x)
{
long long tmp;
is >> tmp;
x = tmp;
return is;
}
friend ostream &operator<<(ostream &os, const mod_int &x)
{
os << x.val();
return os;
}
};
typedef long long ll;
typedef unsigned long long ull;
mt19937 rnd(chrono::system_clock::now().time_since_epoch().count());
constexpr int p = 993244853;
using Hash = mod_int<p>;
// using Hash = ull;
const Hash base = rnd() % 20091119 + 30;
string s, t;
Hash st;
int mnlen;
Hash S[5000020];
Hash T[5000020];
Hash pw[5000020];
inline Hash SUM(const int l, const int r, const Hash *s) { return s[r] - s[l - 1] * pw[r - l + 1]; }
int n, m;
inline bool check(const int l, const int r, const Hash x, const int len, const Hash *S) { return r - l + 1 >= len && SUM(l, l + len - 1, S) == x && SUM(l, r - len, S) == SUM(l + len, r, S); }
inline bool calc(const int L1, const int R1, const int L2, const int R2, const int l1, const int l2)
{
if (mnlen && check(L1, R1, st, mnlen, S) && check(L2, R2, st, mnlen, S))
{
if (check(1, m, st, mnlen, T))
{
for (int i = 0; i <= m; i += l2)
{
if (!((m - i) % l1))
return 1;
}
return 0;
}
}
const Hash s1 = SUM(L1, R1, S);
const Hash s2 = SUM(L2, R2, S);
// int l = 1, r = l2 / l1, okcnt = 0;
// while (l <= r)
// {
// int mid = l + r >> 1;
// if (check(L2, L2 + mid * l1 - 1, s1, l1, S))
// l = (okcnt = mid) + 1;
// else
// r = mid - 1;
// }
int ed = 0;
while (ed <= m)
{
int L = 1, R = (m - ed) / l1, cnt = 0;
while (L <= R)
{
int mid = L + R >> 1;
if (check(ed + 1, ed + mid * l1, s1, l1, T))
L = (cnt = mid) + 1;
else
R = mid - 1;
}
if (ed + cnt * l1 + 1 > m)
return 1;
// bool found = 0;
// int st = ed + (cnt - okcnt) * l1 + 1;
// if (st > ed && st + l2 - 1 <= m && SUM(st, st + l2 - 1, T) == s2)
// {
// ed = st + l2 - 1;
// found = 1;
// }
// if (!found)
// return 0;
bool found = 0;
for (int st = ed + cnt * l1 + 1; st > ed; st -= l1)
{
if (st + l2 - 1 <= m && SUM(st, st + l2 - 1, T) == s2)
{
ed = st + l2 - 1;
found = 1;
break;
}
}
if (!found)
return 0;
}
return 1;
}
void solve()
{
// build();
mnlen = 0;
cin >> n >> m >> s >> t;
s = ' ' + s;
t = ' ' + t;
for (int i = 1; i <= n; i++)
S[i] = S[i - 1] * base + Hash(s[i] - 'a' + 1);
for (int i = 1; i <= m; i++)
T[i] = T[i - 1] * base + Hash(t[i] - 'a' + 1);
for (int i = 1; i <= n; i++)
{
if (n % i == 0 && check(1, n, S[i], i, S))
{
st = S[i];
mnlen = i;
break;
}
}
for (int i = 1; i < n; i++)
putchar('0' ^ (i <= n - i ? calc(1, i, i + 1, n, i, n - i) : calc(i + 1, n, 1, i, n - i, i)));
putchar('\n');
}
int main()
{
pw[0] = Hash(1);
for (int i = 1; i <= 5'000'000; i++)
pw[i] = pw[i - 1] * base;
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
int t;
cin >> t;
while (t--)
solve();
return 0;
}
This is written by Caylex.
#include <bits/stdc++.h>
using namespace std;
template <int P>
class mod_int
{
using Z = mod_int;
private:
static int mo(int x) { return x < 0 ? x + P : x; }
public:
int x;
int val() const { return x; }
mod_int() : x(0) {}
template <class T>
mod_int(const T &x_) : x(x_ >= 0 && x_ < P ? static_cast<int>(x_) : mo(static_cast<int>(x_ % P))) {}
bool operator==(const Z &rhs) const { return x == rhs.x; }
bool operator!=(const Z &rhs) const { return x != rhs.x; }
Z operator-() const { return Z(x ? P - x : 0); }
Z pow(long long k) const
{
Z res = 1, t = *this;
while (k)
{
if (k & 1)
res *= t;
if (k >>= 1)
t *= t;
}
return res;
}
Z &operator++()
{
x < P - 1 ? ++x : x = 0;
return *this;
}
Z &operator--()
{
x ? --x : x = P - 1;
return *this;
}
Z operator++(int)
{
Z ret = x;
x < P - 1 ? ++x : x = 0;
return ret;
}
Z operator--(int)
{
Z ret = x;
x ? --x : x = P - 1;
return ret;
}
Z inv() const { return pow(P - 2); }
Z &operator+=(const Z &rhs)
{
(x += rhs.x) >= P && (x -= P);
return *this;
}
Z &operator-=(const Z &rhs)
{
(x -= rhs.x) < 0 && (x += P);
return *this;
}
Z operator-() { return -x; }
Z &operator*=(const Z &rhs)
{
x = 1ULL * x * rhs.x % P;
return *this;
}
Z &operator/=(const Z &rhs) { return *this *= rhs.inv(); }
#define setO(T, o) \
friend T operator o(const Z &lhs, const Z &rhs) \
{ \
Z res = lhs; \
return res o## = rhs; \
}
setO(Z, +) setO(Z, -) setO(Z, *) setO(Z, /)
#undef setO
friend istream &
operator>>(istream &is, mod_int &x)
{
long long tmp;
is >> tmp;
x = tmp;
return is;
}
friend ostream &operator<<(ostream &os, const mod_int &x)
{
os << x.val();
return os;
}
};
typedef long long ll;
typedef unsigned long long ull;
mt19937 rnd(chrono::system_clock::now().time_since_epoch().count());
constexpr int p = 993244853;
using Hash = mod_int<p>;
// using Hash = ull;
const Hash base = rnd() % 20091119 + 30;
string s, t;
Hash st;
int mnlen;
Hash S[5000020];
Hash T[5000020];
Hash pw[5000020];
// int doit;
inline Hash SUM(const int l, const int r, const Hash *s) { return s[r] - s[l - 1] * pw[r - l + 1]; }
int n, m;
inline bool check(const int l, const int r, const Hash x, const int len, const Hash *S)
{
// doit++;
return r - l + 1 >= len && SUM(l, l + len - 1, S) == x && SUM(l, r - len, S) == SUM(l + len, r, S);
}
inline bool calc(const int L1, const int R1, const int L2, const int R2, const int l1, const int l2)
{
if (mnlen && check(L1, R1, st, mnlen, S) && check(L2, R2, st, mnlen, S))
{
if (check(1, m, st, mnlen, T))
{
for (int i = 0; i <= m; i += l2)
{
if (!((m - i) % l1))
return 1;
}
return 0;
}
}
const Hash s1 = SUM(L1, R1, S);
const Hash s2 = SUM(L2, R2, S);
int l = 1, r = l2 / l1, okcnt = 0;
while (l <= r)
{
int mid = l + r >> 1;
if (check(L2, L2 + mid * l1 - 1, s1, l1, S))
l = (okcnt = mid) + 1;
else
r = mid - 1;
}
const int tt = (n / l1);
int ed = 0;
while (ed <= m)
{
int L = 1, R = (m - ed) / l1, cnt = 0;
int tcnt = 0;
while (tcnt + tt <= R && check(ed + 1, ed + (tcnt + tt) * l1, s1, l1, T))
tcnt += tt;
L = max(L, tcnt);
R = min(R, tcnt + tt - 1);
// cerr << ed << ' ' << L << ' ' << R << '\n';
while (L <= R)
{
int mid = L + R >> 1;
if (check(ed + 1, ed + mid * l1, s1, l1, T))
L = (cnt = mid) + 1;
else
R = mid - 1;
}
if (ed + cnt * l1 + 1 > m)
return 1;
// int st = ed + (cnt - okcnt) * l1 + 1;
// if (st > ed && st + l2 - 1 <= m && SUM(st, st + l2 - 1, T) == s2)
// {
// ed = st + l2 - 1;
// continue;
// }
// return 0;
bool found = 0;
for (int st = ed + (cnt - okcnt) * l1 + 1, cnt = 1; cnt <= 2 && st > ed; st -= l1, cnt++)
{
if (st + l2 - 1 <= m && SUM(st, st + l2 - 1, T) == s2)
{
ed = st + l2 - 1;
found = 1;
break;
}
}
if (!found)
return 0;
}
return 1;
}
void solve()
{
// build();
mnlen = 0;
cin >> n >> m >> s >> t;
s = ' ' + s;
t = ' ' + t;
for (int i = 1; i <= n; i++)
S[i] = S[i - 1] * base + Hash(s[i] - 'a' + 1);
for (int i = 1; i <= m; i++)
T[i] = T[i - 1] * base + Hash(t[i] - 'a' + 1);
for (int i = 1; i <= n; i++)
{
if (n % i == 0 && check(1, n, S[i], i, S))
{
st = S[i];
mnlen = i;
break;
}
}
for (int i = 1; i < n; i++)
putchar('0' ^ (i <= n - i ? calc(1, i, i + 1, n, i, n - i) : calc(i + 1, n, 1, i, n - i, i)));
putchar('\n');
// cerr << doit << '\n';
}
int main()
{
// freopen("out.txt", "r", stdin);
pw[0] = Hash(1);
for (int i = 1; i <= 5'000'000; i++)
pw[i] = pw[i - 1] * base;
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
int t;
cin >> t;
while (t--)
solve();
// cerr << fixed << setprecision(10) << 1.0 * clock() / CLOCKS_PER_SEC << '\n';
return 0;
}
2053H - Delicate Anti-monotonous Operations
Special thanks to LMydd0225 and N_z__ for developing this problem.
What if $$$w = 2$$$? Is it optimal to increase $$$\sum\limits_{i=0}^n [a_i \neq a_{i+1}]$$$ (suppose $$$a_0 = a_{n+1} = 2$$$)?
If $$$w \geq 3$$$, what's the answer to the first question?
If $$$a_i = a_{i+1}$$$, after the operation we can obtain $$$a_{i-1} = a_i$$$ or $$$a_{i+1} = a_{i+2}$$$ (and possibly, both).
Try to think of the whole process reversedly. If $$$w \geq 3$$$, $$$1 \leq a_i \leq w - 1$$$, can you solve the problem?
How many extra operations are required for each $$$1 \leq i \leq n$$$ if $$$a_i = w$$$, in the above scheme you use for $$$a_i \leq w - 1$$$?
Read the Hints.
- $$$w = 2$$$
After any operation, $$$k = \sum\limits_{i=0}^n [a_i \neq a_{i+1}]$$$ won't decrease (suppose $$$a_0 = a_{n+1} = 2$$$). For a fixed $$$k$$$, the maximal $$$\sum a_i = 2n - \frac{1}{2}k$$$ and can be reached by each time turning a $$$[2, 1, 1]$$$ into $$$[2, 2, 1]$$$ (or symmetrically, $$$[1, 1, 2] \rightarrow [1, 2, 2]$$$.
- $$$w \geq 3$$$
- No initial operations can be conducted, or $$$\min(a_i) = w$$$
This case is trivial.
- $$$w \geq 3$$$
- Some initial operations can be conducted
We claim that the answer to the first question is $$$nw - 1$$$. For the second question, let's study some rather easier cases below.
- $$$w \geq 3$$$
- Some initial operations can be conducted
- $$$a_i \neq w$$$
- Some initial operations can be conducted
We pretend that the final sequence is $$$[w, w, \dots, w, (w-1), w, w, \dots, w]$$$, then since $$$(a_i, a_{i+1})$$$ must be different after the operation, the last operation can only occur on $$$[w, (w-1)]$$$ (or $$$[(w-1), w]$$$). And since initially $$$a_i \neq w$$$, each position must have been operated on at least once.
This gives us states such as $$$[w, \dots, w, x, x, w, \dots, w]$$$, $$$[w, \dots, w, y, y, x, w, \dots, w]$$$, etc. To the leftmost positions, we get $$$a_1 = a_2$$$ (essentially based on Hint 3). Also, we get ...... $$$a_{n-1} = a_n$$$? This is if and only if the initial $$$[w, (w - 1)]$$$ is neither at the beginning nor at the end. If the initial $$$[w, (w - 1)]$$$ is at the beginning, we only need $$$a_{n-1} = a_n$$$ to achieve the goal, and symmetrically the same. Less is more. Obviously, we only need to satisfy either $$$a_1 = a_2$$$ or $$$a_{n-1} = a_n$$$, and then use $$$n - 1$$$ more operations to reach the target situation.
How do we get to $$$a_1 = a_2$$$ (symmetrically the same)? Based on Hint 3, we find the smallest $$$x$$$ that satisfies $$$a_x = a_{x+1}$$$, and then follow the example above, again using $$$x - 1$$$ operations to conduct the equality sign to $$$a_1 = a_2$$$.
Lemma 1: We can never choose an index $$$a_i = w$$$, fix it (i.e. avoid changing $$$a_i$$$ in the following operations), and then use some operations to reach $$$\sum a_i = nw - 1$$$ unless $$$[a_1, \ldots, a_i] = [w, \ldots, w]$$$ or $$$[a_i, \ldots, a_n] = [w, \ldots, w]$$$.
Proof: If not so, the array is split into two parts: $$$[a_1, \ldots, a_{i-1}]$$$ and $$$[a_{i+1}, \ldots, a_n]$$$. We have: after some operations, the maximum $$$\sum a_i$$$ we can get for each part are respectively $$$(i-1)w - 1, (n-i)w - 1$$$, and add them up and we get $$$nw - 2$$$, which is less than $$$nw - 1$$$, so it's never optimal.
Lemma 2: Look at the final array $$$a$$$, consisting of $$$n - 1$$$ element $$$w$$$ and $$$1$$$ element $$$(w - 1)$$$. Obtain an array $$$a'$$$ by keeping the elements with the value of $$$w$$$. Denote $$$t_i$$$ as the last round in which $$${a'}_i$$$ was changed to $$$w$$$ (and then become fixed). Then, there exists some $$$k$$$ such that $$$t_1 < t_2 < \dots < t_k > t_{k+1} > \dots > t_{n-1}$$$.
Proof: This follows from Lemma 1.
According to Lemma 2, we can see the pattern that we used above is optimal.
- $$$w \geq 3$$$
- Some initial operations can be conducted
- $$$a_1 \neq w, a_n \neq w$$$
- Some initial operations can be conducted
Basically, the idea remains to reach $$$a_1 = a_2$$$ in the same way first (symmetrically the same), and then to extend to all positions. However, at this point, in the second stage, some problems may arise as follows:
- $$$[\dots \underline{a_k}\ a_{k+1}\ w\ a_{k+3} \dots]$$$
- $$$[\dots \underline{\color{red}{a_{k+1}}\ a_{k+1}}\ w\ a_{k+3} \dots]$$$
- $$$[\dots \color{red}s\ \underline{\color{red}w\ w}\ a_{k+3} \dots]$$$
- $$$[\dots \color{red}{\underline{s\ s}}\ t\ a_{k+3} \dots]$$$
- $$$[\dots \color{red}w\ \underline{\color{red}t\ t}\ a_{k+3} \dots]$$$
- $$$[\dots \color{red}{w\ w}\ \underline{\color{red}{a_{k+3}}\ a_{k+3}} \dots]$$$
In which $$$s, t, w$$$ are three distinct integers in the range $$$[1, w]$$$ (This also explains why we need to specially deal with the $$$w = 2$$$ case). Since we cannot fix $$$a_{k+2} = w$$$ at the beginning (refer to the "Why is it optimal?" spoiler above), we have to first change $$$a_{k+2}$$$ into something not equal to $$$w$$$, and that cost at least $$$2$$$ extra operations, which is shown here.
Do we always need $$$2$$$ extra operations? One may note that if $$$a_i = a_{i+1} = w$$$, in which the two elements are both in the way of expansion, we can only use $$$1$$$ operation to vanish their existence. Formally, if there is a maximum continuous subsegment of $$$w$$$ in the way of expansion, let its length be $$$L$$$, then we will spend $$$\lceil \frac{L}{2} \rceil + [L = 1]$$$ extra operations.
Suppose in the first stage, we pick $$$a_x = a_{x+1}$$$ and keep operating on it until $$$a_1 = a_2$$$. Then after it, $$$\forall 3 \leq k \leq x + 1$$$, $$$a_k$$$ can be an arbitrary number which is different from the initial $$$a_{k-1}$$$, thus we can always force it to be $$$\neq w$$$.
In the above case, only elements $$$[a_{x+2}, \ldots, a_n]$$$ are considered 'in the way of expansion', and symmetrically the same.
- $$$w \geq 3$$$
- Some initial operations can be conducted
- No additional constraints
- Some initial operations can be conducted
It may come to you that if $$$a_1 = w$$$, we can ignore $$$a_1$$$; if $$$a_1 = a_2 = w$$$, we can ignore $$$a_2$$$. Symmetrically the same. And so on... Then we boil the problem down to the case above.
It is correct unless in some rare cases when we ignore all the prefixes and suffixes, there will be no remaining $$$a_i = a_{i+1}$$$; or if we pick any pair $$$a_i = a_{i+1}$$$ as the starting pair in the remaining array, it is not optimal compared to picking an $$$a_k = a_{k+1} = w (a_{k+2} \neq w)$$$ (symmetrically the same). So, we have to special handle the deleted prefix and suffix, once it has a length greater than $$$2$$$.
In summary, the problem can be solved in $$$\mathcal O(n)$$$.
#include <bits/stdc++.h>
#define MAXN 200005
int a[MAXN];
void solve() {
int N, w; scanf("%d%d", &N, &w);
for (int i = 1; i <= N; ++i) scanf("%d", a + i);
if (N == 1) return (void)printf("%d 0\n", a[1]);
if (*std::min_element(a + 1, a + N + 1) == w)
return (void)printf("%lld 0\n", 1ll * w * N);
if (w == 2) {
int ans = N * 2, pans = 0;
for (int i = 1, j = 1; i <= N; i = ++j) if (a[i] == 1) {
--ans; while (j < N && a[j + 1] == 1) ++j; pans += j - i;
}
return (void)printf("%d %d\n", ans, pans);
}
bool flag = true;
for (int i = 1; i < N; ++i) if (a[i] == a[i + 1]) flag = false;
if (flag) return (void)printf("%lld 0\n", std::accumulate(a + 1, a + N + 1, 0ll));
printf("%lld ", 1ll * w * N - 1);
if (std::accumulate(a + 1, a + N + 1, 0ll) == 1ll * w * N - 1) return (void)puts("0");
int ans = 0x3f3f3f3f, l = (a[1] == w ? 2 : 1), r = (a[N] == w ? N - 1 : N);
if ((a[1] == w && a[2] == w) || (a[N] == w && a[N - 1] == w)) {
int Lw = 0, Rw = N + 1;
while (a[Lw + 1] == w) ++Lw; while (a[Rw - 1] == w) --Rw;
int pans = Rw - Lw;
for (int i = Lw + 1, j = i; i < Rw; i = ++j) if (a[i] == w) {
while (j + 1 < Rw && a[j + 1] == w) ++j;
pans += (i == j ? 2 : ((j - i) >> 1) + 1);
}
ans = pans, l = Lw + 1, r = Rw - 1;
}
for (int d = 0; d < 2; std::reverse(a + l, a + r + 1), ++d)
for (int i = l - 1, pre = 0, len = 0; i + 2 <= r; ) {
if (a[i + 1] == a[i + 2])
ans = std::min(r - (i + 1) + r - l - 1 + pre - ((len == 1) && i + 2 < r && a[i + 3] != w ? 1 : 0), ans);
++i; if (a[i] == w) ++len, pre += (len == 1 ? 2 : len == 2 ? -1 : (len & 1)); else len = 0;
}
printf("%d\n", ans);
}
int main() { int T; scanf("%d", &T); while (T--) solve(); return 0; }
2053I1 - Affectionate Arrays (Easy Version)
What is the minimized LIS?
How do you prove that it is an achievable lower bound?
Go for a brute DP first.
We claim that the minimized LIS is $$$\sum a_i$$$. Let $$$p$$$ be $$$\sum a_i$$$.
Since it is required that $$$\operatorname{LIS}(b) = p$$$ while $$$\sum b_i = p$$$, we point out that it is equivalent to each of the prefix sums of the sequence being between $$$[0, p]$$$.
- Sufficiency: $$$\forall X \in [0, p], Y \in [0, p]$$$, $$$X - Y \leq p$$$. Also, we can pick $$$X = p, Y = 0$$$, so it can only be $$$= p$$$.
- Necessity: disproof. If a prefix sum is $$$< 0$$$, then choose the whole array except for this prefix; if a prefix sum is $$$> p$$$, then choose this prefix. Both derive a contradiction of the LIS being greater than $$$p$$$.
Consider dp. Let $$$f_{i,j}$$$ denote, after considering the first $$$i$$$ numbers, the minimum extra sequence length (i.e. the actual length minus $$$i$$$), when the current prefix sum is $$$j$$$. The initial states are $$$f_{0,j} = [j \neq 0]$$$. The transfer is simple too:
It is possible to optimize the transfer to $$$\mathcal O(np)$$$, since for each $$$j$$$, the contribution from at most one $$$k$$$ is special ($$$+0$$$). We can calculate the prefix and suffix $$$\min$$$ for $$$f_{i-1}$$$ and it will be fast to get the dp array in the new row. Then, let's focus on optimizing it to $$$\mathcal O(n)$$$.
We call the set of $$$0 \leq k \leq p$$$ satisfying $$$0 \leq k + a_i \leq p$$$ as the legal interval of $$$i$$$ (denoted as $$$L_i$$$).
It is concluded that the range of $$$f_{i, 0\dots p}$$$ is at most $$$1$$$, and this can be proven by considering the transfer to each of the $$$j$$$ with the $$$k \in L_i$$$ which has the least $$$f_{i-1, k}$$$. Let $$$v_i = \min_{0 \leq j \leq p}(f_{i, j})$$$. We also have: for those $$$j$$$ with $$$f_{i,j} = v_i$$$, they form a consecutive segment in the integer field. Let the segment be covering $$$[l_i, r_i]$$$.
Inductive proof. The essence of the transfer is that it shifts all the DP values $$$= v_{i-1}$$$ by $$$a_i$$$ unit length, and all the other numbers will be updated to $$$v_{i-1} + 1$$$. Then truncates the $$$j \in ((-\inf, 0) \cup (p, +\inf))$$$ part. The consecutive segment remains consecutive. Specially, if $$$[l_{i-1}, r_{i-1}] \cap L_i = \varnothing$$$, then $$$\min_{k \in L_i}(f_{i-1, k}) = v_{i-1} + 1$$$, hence we need to set $$$v_i = v_{i-1} + 1$$$, and $$$l_i, r_i$$$ as the range of $$$j = k + a_i$$$ in which $$$k \in L_i$$$. Otherwise, $$$v_i = v_{i-1}$$$, and $$$l_i, r_i$$$ can be calculated by shifting $$$l_{i-1}, r_{i-1}$$$ by $$$a_i$$$ unit length.
In fact, we only need to maintain three variables $$$l, r, v$$$ to represent the current consecutive segment and the current value field. Therefore, this problem can be easily solved in $$$\mathcal O(n)$$$.
#include <bits/stdc++.h>
namespace FastIO {
template <typename T> inline T read() { T x = 0, w = 0; char ch = getchar(); while (ch < '0' || ch > '9') w |= (ch == '-'), ch = getchar(); while ('0' <= ch && ch <= '9') x = x * 10 + (ch ^ '0'), ch = getchar(); return w ? -x : x; }
template <typename T> inline void write(T x) { if (!x) return; write<T>(x / 10), putchar((x % 10) ^ '0'); }
template <typename T> inline void print(T x) { if (x > 0) write<T>(x); else if (x < 0) putchar('-'), write<T>(-x); else putchar('0'); }
template <typename T> inline void print(T x, char en) { print<T>(x), putchar(en); }
}; using namespace FastIO;
#define MAXN 3000001
int a[MAXN];
void solve() {
int N = read<int>(); long long p = 0, l = 0, r = 0, v = 0;
for (int i = 1; i <= N; ++i) p += (a[i] = read<int>());
for (int i = 1; i <= N; ++i) if (a[i] >= 0) {
l += a[i], r = std::min(r + a[i], p);
if (l > r) ++v, l = a[i], r = p;
} else {
a[i] = -a[i];
r -= a[i], l = std::max(l - a[i], 0ll);
if (l > r) ++v, l = 0, r = p - a[i];
}
print<int>(v + N + (int)(r != p), '\n');
}
int main() { int T = read<int>(); while (T--) solve(); return 0; }
2053I2 - Affectionate Arrays (Hard Version)
Try insert numbers into spaces between the elements of $$$a$$$ (including the beginning and the end). Note that an array be can be formed in multiple ways (for example, you can insert a number $$$x$$$ to the left or right of the original number $$$x$$$ in array $$$a$$$). What's the number of different ways?
It's actually the "value", that is, the number of occurrances of $$$a$$$. Use the fact that "only one number can be inserted into each space" to prove.
Read the editorial for I1 and the hints first.
According to the hint, you can count the number of ways to insert the new numbers into the space, so the dp and transitions are similar to those in problem I1.
We can add an additional dp array, $$$g_{i, j}$$$ representing the number of different ways when everything meets the description of $$$f_{i, j}$$$. Let's see from which values it can be transferred:
- If $$$f_{i, j} = v_i$$$, then $$$f_{i, j}$$$ can only be transferred from $$$f_{i-1, j-a_i}$$$. That is, $$$g_{i, j} = g_{i-1, j-a_i}$$$.
- If $$$f_{i, j} = v_i + 1$$$, then $$$f_{i, j} = \sum_{k \in L_i, f_{i-1, k} = f_{i, j} - 1} g_{i-1, k}$$$.
We can use some tags and a Deque to maintain the whole process, so the amortized time complexity is $$$\mathcal O(n)$$$.
#include <bits/stdc++.h>
namespace FastIO {
template <typename T> inline T read() { T x = 0, w = 0; char ch = getchar(); while (ch < '0' || ch > '9') w |= (ch == '-'), ch = getchar(); while ('0' <= ch && ch <= '9') x = x * 10 + (ch ^ '0'), ch = getchar(); return w ? -x : x; }
template <typename T> inline void write(T x) { if (!x) return; write<T>(x / 10), putchar((x % 10) ^ '0'); }
template <typename T> inline void print(T x) { if (x > 0) write<T>(x); else if (x < 0) putchar('-'), write<T>(-x); else putchar('0'); }
template <typename T> inline void print(T x, char en) { print<T>(x), putchar(en); }
}; using namespace FastIO;
const int MOD = 998244353;
namespace Modint {
inline int add(int x, int y) { return (x += y) >= MOD ? x - MOD : x; }
inline int sub(int x, int y) { return x < y ? x - y + MOD : x - y; }
inline int mul(int x, int y) { return 1ll * x * y % MOD; }
inline int pow(int x, int y) { int r = 1; for (; y; y >>= 1, x = mul(x, x)) if (y & 1) r = mul(r, x); return r; }
inline int inv(int x) { return pow(x, MOD - 2); }
};
struct modint {
int v;
modint (int x = 0) : v(x) { /* for debug only. assert(0 <= x && x < MOD); */ }
inline int get() { return v; }
modint operator - () const { return v ? MOD - v : 0; }
modint operator + (const modint &k) const { return Modint::add(v, k.v); }
modint operator - (const modint &k) const { return Modint::sub(v, k.v); }
modint operator * (const modint &k) const { return Modint::mul(v, k.v); }
modint operator / (const modint &k) const { return Modint::mul(v, Modint::inv(k.v)); }
modint pow(const modint &k) const { return Modint::pow(v, k.v); }
modint inverse() const { return Modint::inv(v); }
modint operator += (const modint &k) { (v += k.v) >= MOD && (v -= MOD); return *this; }
modint operator -= (const modint &k) { (v -= k.v) < 0 && (v += MOD); return *this; }
modint operator *= (const modint &k) { return v = Modint::mul(v, k.v); }
modint operator /= (const modint &k) { return v = Modint::mul(v, Modint::inv(k.v)); }
};
struct Node {
int f; modint g; long long len;
Node () {}
Node (int F, int G, long long L) : f(F), g(G), len(L) {}
Node (int F, modint G, long long L) : f(F), g(G), len(L) {}
}; std::deque<Node> Q;
#define MAXN 3000001
int a[MAXN];
void solve() {
int N = read<int>(); long long p = 0, l = 0, r = 0, v = 0;
for (int i = 1; i <= N; ++i) p += (a[i] = read<int>());
for (int i = 1; i <= N; ++i) assert (std::abs(a[i]) <= p);
Q.clear(); Q.push_back(Node(0, 1, 1)), Q.push_back(Node(1, 1, p));
modint gv = 1, gz = p % MOD, tv = 0, tz = 0;
for (int i = 1; i <= N; ++i) if (a[i] >= 0) {
for (long long ls = a[i]; ls > 0; ) {
Node k = Q.back(); Q.pop_back();
if (ls < k.len) Q.push_back(Node(k.f, k.g, k.len - ls)), k.len = ls;
(k.f == v ? gv : gz) -= k.g * (k.len % MOD), ls -= k.len;
}
l += a[i], r = std::min(r + a[i], p);
if (l > r) ++v, l = a[i], r = p, gv = gz, tv = tz, gz = tz = 0;
gz += -tz * (a[i] >= MOD ? a[i] - MOD : a[i]);
if (a[i] > 0) Q.push_front(Node(v + 1, -tz, a[i]));
tz += gv + tv * ((r - l + 1) % MOD);
} else if (a[i] < 0) {
a[i] = -a[i];
for (long long ls = a[i]; ls > 0; ) {
Node k = Q.front(); Q.pop_front();
if (ls < k.len) Q.push_front(Node(k.f, k.g, k.len - ls)), k.len = ls;
(k.f == v ? gv : gz) -= k.g * (k.len % MOD), ls -= k.len;
}
r -= a[i], l = std::max(l - a[i], 0ll);
if (l > r) ++v, l = 0, r = p - a[i], gv = gz, tv = tz, gz = tz = 0;
gz += -tz * (a[i] >= MOD ? a[i] - MOD : a[i]), Q.push_back(Node(v + 1, -tz, a[i])), tz += gv + tv * ((r - l + 1) % MOD);
}
print<int>((Q.back().g + (r == p ? tv : tz)).get(), '\n');
}
int main() { int T = read<int>(); while (T--) solve(); return 0; }
Try to solve the initial problem: count the number of valid array $$$b$$$ for $$$n\le 500$$$.
Consider $$$f_{i,j,k}$$$: the number of ways to fill the first $$$i$$$ elements of $$$b$$$, which contains at most $$$j$$$ first elements from $$$a$$$ as a subsequence, and the sum of the first $$$i$$$ elements is $$$k$$$.
Try to optimize this from $$$O(n^2s^2)$$$ to $$$O(n^2s)$$$, and then $$$O(\rm{poly}(n))$$$, and then $$$O(n^3)$$$.










