Introduction
A classical problem reads:
Count the paths from $$$(0,0)$$$ to $$$(m,n)(n>m>0)$$$ that doesn't go through $$$y=x$$$ (the path can touch the line). One can only move up or right by $$$1$$$ in one move.
The problem can also be described as:
Count binary strings that consist of $$$m$$$ zeros and $$$n$$$ ones $$$(n\ge m)$$$, such that in every prefix of the string, the number of zeros doesn't exceed the number of ones.
Consider how to count paths from $$$(0,0)$$$ to $$$(m,n)$$$ without the intersection restriction. To get to $$$(m,n)$$$, we must move up $$$n$$$ times and move right $$$m$$$ times. In other words, we need to permute $$$n$$$ right and $$$m$$$ up, whose quantity is
To find the answer, we can try to count the paths that go through $$$y=x$$$, and this is when the reflection principle is utilized. The principle says:
Given point $$$A,B$$$ at the same side of line $$$l$$$, the number of paths from $$$A$$$ to $$$B$$$ that intersect with $$$l$$$ is equal to that of paths from $$$A^\prime$$$ to $$$B$$$, where $$$A^\prime$$$ is the reflection point through $$$l$$$.
To show why it is correct, we should first note that a path from $$$A^\prime$$$ to $$$B$$$ must intersect with $$$y=x$$$. Say at point $$$P$$$ the path first intersect with $$$y=x$$$, we can reflect the path from $$$A^\prime$$$ to $$$P$$$ through $$$l$$$ and get a path from $$$A$$$ to $$$B$$$, and vice versa. This indicates that the intersecting paths from $$$A$$$ to $$$B$$$ and the paths from $$$A^\prime$$$ and $$$B$$$ are one-to-one corresponded, and the quantity of the two are the same.
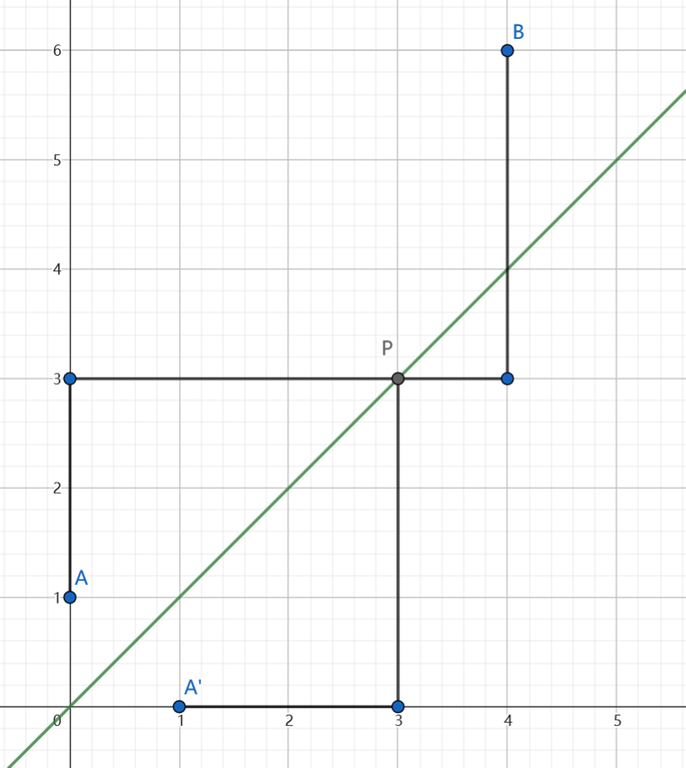
Back to our problem. Going through $$$y=x$$$ is the same as intersecting with $$$y=x-1$$$ in this case, so $$$(0,0)$$$ can reflected to $$$(1,-1)$$$, and the number of intersecting path is $$$\binom{m+n}{m-1}$$$. Therefore, the answer to the problem is
In particular, when $$$n=m$$$, the formula becomes
which is the Catalan number.
Examples
105390D - String From Another World











Auto comment: topic has been updated by -firefly- (previous revision, new revision, compare).
how can i reach that lvl?
Auto comment: topic has been updated by -firefly- (previous revision, new revision, compare).
Going through y=x is the same as intersecting with y=x−1 in this case, so (0,0) can reflected to (1,−1) ,
How so?
nvm. i got it.
ZZ!!
BaoBao!!
its amazing!!
that's an very interesting solution for me. IQ+1
n in second tutorial suppose to be m isn't it? at the formula $$$ \binom{n}{i - k} - \binom{n}{i - k - 1} $$$
Shouldn't this tutorial be a lot more elaborate? Rather difficult to digest for someone reading this for the first time. While the problem selections are good and the content can perhaps still be inferred from what little has been given, the reflection property feels underexplained and the single diagram provided is hardly helpful.