Hi. I will explain my approach to solve this hard and counter-intuitive problem.
The problem
You've got some telephone numbers. Each number is dialed a given amount of times. You would need to do an amount of key presses to dial all numbers, that is well defined. However there is an amount of special buttons that can be used to type several digits at once. The buttons can only be used at the start of a number (before manually typing anything). Buttons presses does not count as digit press. Buttons can only be used once per number. You need to decide how to place k buttons to minimize total digit presses.
First insight
We need to build a trie structure of the numbers, this will allow us to exploit numbers that have something in common
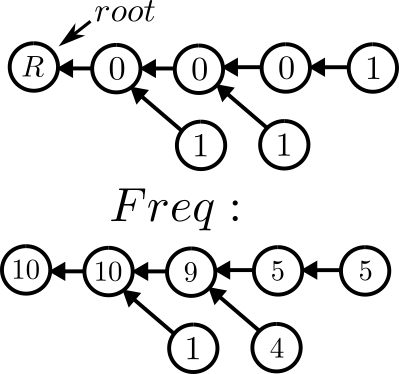
(Example of trie of test case 1)
Need of DP
We should note some kind of DP should be used using sub-trees. The sub-problem could be defined like
"Solving sub-tree rooted at i using j buttons on strings belonging to that sub-tree.
But there is a technical problem defining DP like that. Although it is logically valid to think "solving" as "assigning buttons" to strings on that sub-tree, we need to store some number to represent that way of "assigning buttons" on DP_{ij}. The natural value would be "total key presses" to solve the sub-tree i using j buttons. But think about the characters of strings belonging to sub-tree but that are outside it. Should we consider it on sub-problem value? Yes or No?
I have though about that fact some time and realized that we can't solve the problem no matter the answer is Yes or No.
If the answer is Yes and we consider the outside characters of strings then DP of a smaller sub-trees is depending of DP of bigger sub-trees which is a contradiction. (Think if we use a button over the root of a sub-tree, then the sub-tree DP value changes)
If the answer is No, then and we only consider key presses used on that sub-tree then there is another problem. Imagine we are solving a sub-tree i with j buttons and we assume we have solved all children of sub-tree rooted at i root for all j' ≤ j. If we use a button ending on i we can't compute the total key presses of sub-tree rooted at i because it depends on the amount of strings belonging to sub-trees rooted at i children that are currently not being helped by any button, that do not depend on the sub-trees rooted at children of i DP values. It is another variable that should be added as another DP variable. But I have not analysed if this way the problem could be solved, maybe is too hard.
Thus the conclusion is that one way or another we need to add another variable to characterize our DP sub problem, otherwise the sub-problems can't be connected properly.
We use the DP that answer YES to the question made above. We need to solve the fact stated about the dependency of smaller sub-trees with bigger sub-trees by adding a variable.
DP would be defined like this
DPi, j, k: Amount of key presses to dial all strings belonging to sub-tree rooted at i using j buttons on them. (And k??)
This of course depends of buttons used upside i. But there is a simplification. It depends in particular only on the lowest button used upside i, not every one.
So that is the variable we need to make DP well defined, the lowest button used upside i. That is the only information about upper nodes that our sub-tree uses.
DPi, j, k: Amount of key presses to dial all strings belonging to sub-tree rooted at i using j buttons on them, considering the lowest button used up-side i ends at node k
And now when we solve highest sub-trees using lower sub-trees, they don't depend on highest sub-trees, because when we solve a higher sub-tree using a lower sub-tree we know k value that would correspond to the children DP solution we are using.








 . We need all
. We need all 

