I'm referring to this binary search
int L = 0, R = n;
while (L < R) {
int m = (l+r)/2;
if (F(m)) {
L = m+1;
} else {
R = m;
}
} return L;
Why conventional Binary seach sucks:
A. There are multiple potential off-by-one errors in it. B. It looks ugly. C. It's not the most intuitive approach.
My binary search:
int x = 0, j = *closest power of two higher than the desired range length*;
while (j/=2) {
if (!F(x+j)) x += j;
} return x+1;
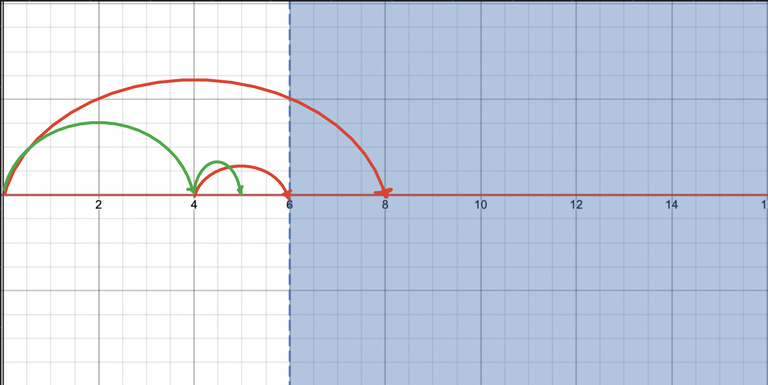
The intuition: We have a function F(x) that begins to be satisfied at some point P. We want to identify P. We'll aim to go as close to it as possible without touching it, so we'll jump j steps forward and see if we touch the satasfied region; if we do, we won't jump; if we don't, we will. This will put us one step behind P, so we will just add one.
The picture shows an example where the range is 16 and the function is satisfied when x >= 6. We'll attempt leaping a size 8 jump, but the function will be satisfied at that time, so we won't. Then we'll try a size 4 leap and succeed, and so on. Finally, x = 5 represents the greatest x at which the function is not satisfied.
This method achieves the exact same purpose without any areas for off by one errors and I find it much more intuitive than the standared range binary search.











Will
j=n;also work, if I am too lazy to find the appropriate power of 2?I think it should work too.Can you try $$$n = 31$$$, where the answer is supposed to be $$$30$$$?
This indeed does output
27instead of 30. Good find. What'd be a quick fix? One could replaceif(F(x+j))withwhile(F(x+j)). (Or one could just always usej=1<<30?)Yes, the
while (F(x + j))is a standard fix. For a reference, see this blog.This technique is already discussed once on this blog, but I did think it's significant enough to have its own post. One interesting thing about this technique that hasn't been mentioned
there or(UPD: It's linked there) here, is that this would probably be the only method you would be using when you binary search on a BIT. (You can think of how it's possible by thinking of how the BIT works.)UPD again: oh yeah also you can extend this to real values, where the jumping distance starts with $$$0.5(r-l)$$$
It should be clear from the discussion in that post on how to implement binary search iteratively on a segment tree. Also, I had linked a post about binary lifting on Fenwick trees there too, which does the same kind of binary search.
It's just BS with binary lifting, isn't it?
yes it's probably called meta binary search
It's not a meta one. It's just called binary lifting. Congrats to the blog writer that he discovered the method by himself.
I'm really surprised no one mentioned the technique is explained here: Competitive Programmer’s Handbook.
Anyways the book is extremely recommended if you have time take a look at it.
The author of the blog I linked in this comment is the author of that book, so yeah. I agree about the book, it's great for beginners.
your binary search doesnt work try n=31
I recommend you read the other comments in this comment-thread.
Also the algorithm from the blog author should also work with $$$n=31=16+8+4+2+1$$$ because $$$j=32$$$.
You can just use the conventional way but make it R-the precision required and L=M instead to avoid any off by one errors. Also, I feel binary search was intuitive as it’s probably the only algorithm I was able to come up with before knowing what it was.
Clearly this binary search implementation is meant for finding the maximum value of x, what about finding the minimum?