В одном комментарие к одному контесту я опрометчиво упомянул о свойстве следа матрицы и записал:
tr(A^2) mod 2 = (tr(A)*tr(A)) mod 2
Сегодня, прочитав вопрос, я осознал, что мог запутать людей. Спасибо NuM.
Почему?
Конечно же всем наверняка известна формула:
det(A·B) = det(A)·det(B),
где A и B полагаются быть одинаковых размерностей и квадратными (для прямоугольных считать детерминант я еще не научился)
Так вот со следом матрицы это в общем случае неверно.
T.е. 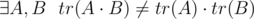
Например, для матрицы тождественного оператора:
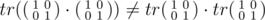
Виноват.
Имелось ввиду свойство: 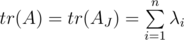 , где AJ — жордановая форма матрицы A, а λi — собственное число.
, где AJ — жордановая форма матрицы A, а λi — собственное число.
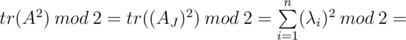
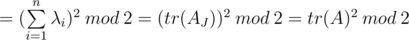
Как-то так. Извините, если кого запутал. Очень надеюсь, что это кому-то помогло :)
UPD: Спасибо vadimmm за найденные ошибки











Положим U, T — операторы состоящих из
собственныхкорневых векторов матриц А, A2 соответственно. Известно что:A = U(A)JU - 1 и A2 = T(A2)JT - 1,
Тогда по свойству tr(ABC) = tr(BCA) имеем:
tr((A2)J) = tr(A2) = tr(U(A)JU - 1U(A)JU - 1) = tr(U(AJ)2U - 1) = tr((AJ)2U - 1U) = tr((AJ)2)
подробней можно почитать здесь: раз, два
Но ведь A2 = V - 1(A2)JV. Почему U = V?
Они не равны :) Я пишу ответ )
Ясно, спасибо. Только U, T состоят из корневых векторов.
Верно, спасибо. Ведь там могут быть и присоединенные вектора.