brunomont's blog

Tiny Dynamic Convex Hull Implementation
By brunomont, history, 21 month(s) ago, In English
TL;DR

Hello, Codeforces!

I recently had to implement a dynamic convex hull (that supports insertions of points online), and I think the implementation got really small, comparable even to standard static convex hull implementations, and we get logarithmic inclusion query for free. We can:

  1. Add a point to the convex hull in $$$\mathcal O(\log n)$$$ amortized time, with $$$n$$$ being the current hull size;
  2. Check if some point belongs to the hull (or border) in $$$\mathcal O(\log n)$$$ time.

Upper Hull

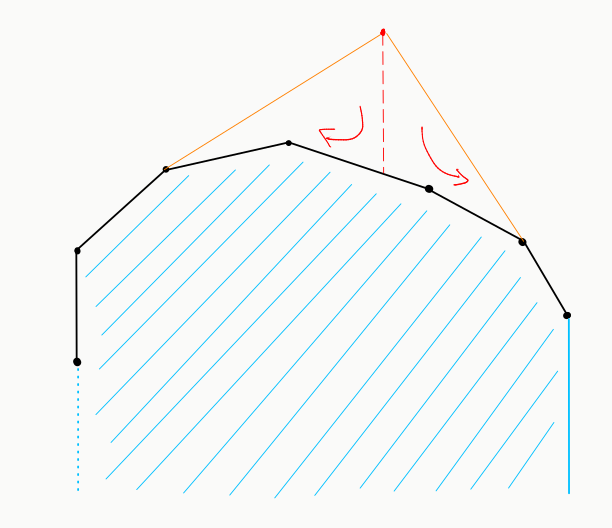
We can maintain the upper hull in a std::set (see below for image, upper hull is in black). We define the region that is under the upper hull as the region in blue, that is, the region that is, well... under. Note, however, that this region is open on the left.

To add a point (red) to the upper hull, we check if it is inside the blue region. If it is, we do nothing. If not, we need to add it, but we might need to remove some points so it continues to be convex. This is done by projecting the red point down (using lower_bound on our set) and iteratively removing points to the right and to the left, while they satisfy the corresponding direction condition.

Point struct
bool ccw(pt p, pt q, pt r) { // counter-clockwise
	return (q-p)^(r-q) > 0;
}

struct upper {
	set<pt> se;
	set<pt>::iterator it;

	int is_under(pt p) { // 1 -> inside ; 2 -> border
		it = se.lower_bound(p);
		if (it == se.end()) return 0;
		if (it == se.begin()) return p == *it ? 2 : 0;
		if (ccw(p, *it, *prev(it))) return 1;
		return ccw(p, *prev(it), *it) ? 0 : 2;
	}
	void insert(pt p) {
		if (is_under(p)) return;

		if (it != se.end()) while (next(it) != se.end() and !ccw(*next(it), *it, p))
			it = se.erase(it);
		if (it != se.begin()) while (--it != se.begin() and !ccw(p, *it, *prev(it)))
			it = se.erase(it);

		se.insert(p);
	}
};

Convex Hull

Now, to implement the full convex hull, we just need an upper and lower hull. But we do not need to implement the lower hull from scratch: we can just rotate the points $$$\pi$$$ radians and store a second upper hull!

Be careful: if the hull has size 1, the point will be represented in both upper and lower hulls. If the hull has size at least 2, then both the first and last points in the upper hull will also appear in the lower hull (in last and first position, respectively). The size() function below is adjusted for this.

struct dyn_hull { // 1 -> inside ; 2 -> border
	upper U, L;

	int is_inside(pt p) {
		int u = U.is_under(p), l = L.is_under({-p.x, -p.y});
		if (!u or !l) return 0;
		return max(u, l);
	}
	void insert(pt p) {
		U.insert(p);
		L.insert({-p.x, -p.y});
	}
	int size() {
		int ans = U.se.size() + L.se.size();
		return ans <= 2 ? ans/2 : ans-2;
	}
};

Conclusion

This implementation is considerably small and also not too slow (the constant factor of std::set operations is not small, but if is in function of the hull size, which in some applications can me small). We also get the logarithmic time query to check if some point is inside the hull.

Removing a point from the convex hull is much trickier, and since our runs in amortized logarithmic time, this can not be modified to support removals.

  • Vote: I like it
  • +157
  • Vote: I do not like it

»
21 month(s) ago, # |
  Vote: I like it 0 Vote: I do not like it

Hi brunomont,

The idea is nice but there is a bug. In the is_under method, when you check it == se.begin() you should check whether the point lies below the left vertex. For example, if the leftmost point of the hull is $$$(0, 0)$$$, your code will return not below for the point $$$(0, -1)$$$.

Also, instead of the bool ccw function, I prefer to use a int turn function that does not compare to zero. Then you can use it to compare to zero with >, >=, < or <=, depending on your problem. Positive sign means strictly ccw, zero means collinear, negative means strictly cw. This can then be extended to your is_under function pretty easily. If you let positive denote inside (or below), zero in the border and negative outside (or above) you need one less call to ccw (simply return its value). Similarly, you would then be able return min(u, l) from the is_inside of dyn_hull without any extra conditional.

I am open to discussing more the implementation if you want. I am preparing my notebook for the ICPC regional and I may include this.

→ Reply
  • »
    »
    21 month(s) ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Actually, to make it more intutitive, negative should mean below, zero border and positive outside.

    → Reply
  • »
    »
    21 month(s) ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Also, if at some point you want to admit collinear points into the hull you should be careful with the size function. You will have all the points repeated whenever the convex hull is a line (which may or may not be what you want).

    → Reply
  • »
    »
    21 month(s) ago, # ^ |
      Vote: I like it +13 Vote: I do not like it

    Hi!

    This is not a bug, it is how I defined the region under the upper hull: Note, however, that this region is open on the left. If I were to include those points, then the convex hull would not work as I wanted it to (so that the smallest and largest point are on both hulls). I am pretty sure it would not work consistently (sometimes there would be repeated points on upper and lower hulls, sometimes there would not be).

    Yeah, I agree about the ccw function. I did it like that to be consistent with the rest of my ICPC notebook.

    → Reply
    • »
      »
      »
      21 month(s) ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      I can see why one would want the region to be open on one side (this is better for partitioning the space if you use multiple upper hulls). Regarding the second part, I guess it's because you use the is_below inside insert, right? Thus, you need to mark those points as outside the hull or you discard them while inserting. I am not sure you could end up with repeated points, though.

      Hence, one could define the lower (with border) part as the set of points that does not modify the hull when inserted, and this does not include the points strictly below the leftmost point. Right?

      Regarding the ccw function, I actually use turn all throughout my notebook. Because in some problems you look for >= and in others for >. Plus, if you do so you do not need to code a collinear function. In this case in particular, I think the negative, null and positive as results are pretty intuitive. The function can then be called position or something like that.

      → Reply
      • »
        »
        »
        »
        21 month(s) ago, # ^ |
        ← Rev. 2   Vote: I like it +5 Vote: I do not like it

        This is what I have. (Notice the hint when inserting in the set):

        struct DynUpperHull {
  set<ipt> hull;
  set<ipt>::iterator it;

  // nve means below, 0 means border, pve means above or outside
  int position(ipt p) {
    it = hull.lower_bound(p);
    if (it == hull.end()) return 1;
    if (it == hull.begin()) return p != *it;
    return turn(p, *prev(it), *it);
  }
  void insert(ipt p) {
    if (position(p) < 0) return;
    if (it != hull.end()) {
      while (next(it) != hull.end() and turn(p, *it, *next(it)) >= 0) {
        it = hull.erase(it);
      }
    }
    if (it != hull.begin()) {
      while (--it != hull.begin() and turn(*prev(it), *it, p) >= 0) {
        it = hull.erase(it);
      }
      ++it;
    }
    hull.insert(it, p);
  }
};

struct DynHull {
  DynUpperHull upp, low;

  int position(ipt p) { return max(upp.position(p), low.position(-p)); }
  void insert(ipt p) {
    upp.insert(p);
    low.insert(-p);
  }
  int size() {
    int ans = upp.hull.size() + low.hull.size();
    return ans - 1 - (ans > 2);
  }
};
        → Reply