Hope you liked the problems!
How many operations are needed to make $$$a_i \le a_{i + 1}$$$ if initially, $$$a_i > a_{i + 1}$$$?
#include <bits/stdc++.h>
#define all(x) (x).begin(), (x).end()
#define allr(x) (x).rbegin(), (x).rend()
#define gsize(x) (int)((x).size())
const char nl = '\n';
typedef long long ll;
typedef long double ld;
using namespace std;
void solve() {
int n;
cin >> n;
vector<int> a(n);
for (int i = 0; i < n; i++) cin >> a[i];
int ans = 0;
for (int i = 0; i < n - 1; i++) {
if (a[i] > a[i + 1]) {
ans = max(ans, a[i]);
}
}
cout << ans << nl;
}
int main() {
ios::sync_with_stdio(0); cin.tie(0);
int T;
cin >> T;
while (T--) {
solve();
}
}
Consider the case $$$n = 1$$$ separately.
Count the number of elements equal to $$$1$$$.
Find the sum of the array.
When there are a lot of elements equal to $$$1$$$ and the sum is not very big, the answer is no.
#include <bits/stdc++.h>
#define all(x) (x).begin(), (x).end()
#define allr(x) (x).rbegin(), (x).rend()
#define gsize(x) (int)((x).size())
const char nl = '\n';
typedef long long ll;
typedef long double ld;
using namespace std;
void solve() {
int n;
cin >> n;
vector<int> a(n);
for (int i = 0; i < n; i++) cin >> a[i];
ll sum_a = 0, cnt_1 = 0;
for (int x: a) {
sum_a += x;
if (x == 1) cnt_1++;
}
if (sum_a >= cnt_1 + n && n > 1) {
cout << "YES" << nl;
} else {
cout << "NO" << nl;
}
}
int main() {
ios::sync_with_stdio(0); cin.tie(0);
int T;
cin >> T;
while (T--) {
solve();
}
}
Binary search on the answer.
Check if it is possible to have $$$\max(a_1,\ldots, a_n) \ge x$$$ for some $$$x$$$.
Fix some possible index that will be the position of the maximum in the final array.
#include <bits/stdc++.h>
#define all(x) (x).begin(), (x).end()
#define allr(x) (x).rbegin(), (x).rend()
#define gsize(x) (int)((x).size())
const char nl = '\n';
typedef long long ll;
typedef long double ld;
using namespace std;
void solve() {
ll n, k;
cin >> n >> k;
vector<ll> a(n);
for (int i = 0; i < n; i++) cin >> a[i];
ll lb = 0, ub = *max_element(all(a)) + k, ans = 0;
while (lb <= ub) {
ll tm = (lb + ub) / 2;
bool good = false;
for (int i = 0; i < n; i++) {
vector<ll> min_needed(n);
min_needed[i] = tm;
ll c_used = 0;
for (int j = i; j < n; j++) {
if (min_needed[j] <= a[j]) break;
if (j + 1 >= n) {
c_used = k + 1;
break;
}
c_used += min_needed[j] - a[j];
min_needed[j + 1] = max(0LL, min_needed[j] - 1);
}
if (c_used <= k) good = true;
}
if (good) {
ans = tm;
lb = tm + 1;
} else {
ub = tm - 1;
}
}
cout << ans << nl;
}
int main() {
ios::sync_with_stdio(0); cin.tie(0);
int T;
cin >> T;
while (T--) solve();
}
What can you say about index $$$j$$$ if the number of inversion in $$$[p_i, p_{i + 1}, \ldots, p_{j - 1}]$$$ is the same as in $$$[p_i, p_{i + 1}, \ldots, p_j]$$$?
Define a function to calculate $$$f(l, r)=$$$ the position of the maximum in $$$[p_l, p_{l + 1}, \ldots, p_{r}]$$$.
Divide and conquer.
#include <bits/stdc++.h>
#define all(x) (x).begin(), (x).end()
#define allr(x) (x).rbegin(), (x).rend()
#define gsize(x) (int)((x).size())
const char nl = '\n';
typedef long long ll;
typedef long double ld;
using namespace std;
int query(int l, int r) {
if (l == r) return 0;
cout << "? " << l << ' ' << r << endl;
int res;
cin >> res;
return res;
}
// Finds max on p[l; r]
int solve(int l, int r) {
if (l == r) return l;
int m = (l + r) / 2;
int a = solve(l, m);
int b = solve(m + 1, r);
int r1, r2;
r1 = query(a, b - 1);
r2 = query(a, b);
if (r1 == r2) {
return b;
} else {
return a;
}
}
void solve() {
int n;
cin >> n;
int ans = solve(1, n);
cout << "! " << ans << endl;
}
int main() {
ios::sync_with_stdio(0); cin.tie(0);
int T;
cin >> T;
while (T--) {
solve();
}
}
1856E1 - PermuTree (easy version)
Fix the value of $$$\operatorname{lca}(u, v)$$$.
You can solve the problem independently for each value of $$$\operatorname{lca}(u, v)$$$.
Do dynamic programming.
For each subtree of $$$\operatorname{lca}(u, v)$$$, we only care about how many vertices are $$$>$$$ or $$$<$$$ less than $$$a_{\operatorname{lca}(u, v)}$$$.
This dynamic programming solution can actually be made to work in $$$\mathcal{O}(n^2)$$$.
#include <bits/stdc++.h>
#define all(x) (x).begin(), (x).end()
#define allr(x) (x).rbegin(), (x).rend()
#define gsize(x) (int)((x).size())
const char nl = '\n';
typedef long long ll;
typedef long double ld;
using namespace std;
const int maxn = 1000000;
vector<int> g[maxn];
int s[maxn];
ll ans = 0;
void dfs(int v, int p = -1) {
vector<ll> a;
s[v] = 1;
for (int u: g[v]) {
if (u == p) continue;
dfs(u, v);
s[v] += s[u];
a.push_back(s[u]);
}
vector<ll> dp(s[v]);
ll cs = 0;
for (int x: a) {
for (ll i = cs + x; i >= 0; i--) {
for (ll pr = min(cs, i); pr >= max(0LL, i - x); pr--) {
ll j = i - pr;
dp[i] = max(dp[i], dp[pr] + j * (cs - pr) + pr * (x - j));
}
}
cs += x;
}
ans += *max_element(all(dp));
dp.clear();
a.clear();
}
int main() {
ios::sync_with_stdio(0); cin.tie(0);
int n;
cin >> n;
for (int i = 1; i < n; i++) {
int x;
cin >> x;
g[x - 1].push_back(i);
}
dfs(0);
cout << ans << nl;
}
1856E2 - PermuTree (hard version)
Read hints for the easy version.
For each $$$\operatorname{lca}(u, v)$$$, we actually need to do subset sum on the subtree sizes.
If there is a very subtree that is bigger than the sum of the sizes of the other subtrees, you don't have to do subset sum.
Optimize subset sum to $$$\mathcal{O}(s \sqrt s)$$$, where s is the sum of the sizes of the subtrees for some fixed $$$\operatorname{lca}(u, v)$$$.
Use bitset to optimize subset sum even more.
#include <bits/stdc++.h>
#define all(x) (x).begin(), (x).end()
#define allr(x) (x).rbegin(), (x).rend()
#define gsize(x) (int)((x).size())
const char nl = '\n';
typedef long long ll;
typedef long double ld;
using namespace std;
const int maxn = 1000000;
vector<int> g[maxn];
int s[maxn];
ll ans = 0;
vector<ll> b;
ll closest;
template <int len = 1>
void subset_sum(int n) {
if (n >= len) {
subset_sum<std::min(len*2, maxn)>(n);
return;
}
bitset<len> dp;
dp[0] = 1;
for (ll x: b) {
dp = dp | (dp << x);
}
ll cv = n;
closest = 0;
for (int i = 0; i <= n; i++) {
if (dp[i] && abs(i - (n - i)) < cv) {
closest = i;
cv = abs(i - (n - i));
}
}
}
ll solve(vector<ll> &a) {
if (a.empty()) return 0;
sort(allr(a));
ll cs = 0;
for (ll x: a) cs += x;
if (a[0] * 2 >= cs) {
return a[0];
}
int n = gsize(a);
a.push_back(0);
b.clear();
int pi = 0;
for (int i = 1; i <= n; i++) {
if (a[i] != a[i - 1]) {
ll cnt = i - pi;
ll x = a[i - 1];
ll j = 1;
while (j < cnt) {
b.push_back(x * j);
cnt -= j;
j *= 2;
}
b.push_back(x * cnt);
pi = i;
}
}
subset_sum(cs);
return closest;
}
void dfs(int v, int p = -1) {
vector<ll> a;
s[v] = 1;
for (int u: g[v]) {
if (u == p) continue;
dfs(u, v);
s[v] += s[u];
a.push_back(s[u]);
}
ll x = solve(a);
ans += x * (s[v] - 1 - x);
a.clear();
}
int main() {
ios::sync_with_stdio(0); cin.tie(0);
int n;
cin >> n;
for (int i = 1; i < n; i++) {
int x;
cin >> x;
g[x - 1].push_back(i);
}
dfs(0);
cout << ans << nl;
}
UPD: Tutorial for E1 has been added.
UPD2: Tutorial for E2 has been added.
Can non-custom bitsets even pass on E2? if not the problem is just bad imo
The model solution doesn't use custom bitsets.
I think the only "custom" thing it requires is modifying bitset's size via templates.
I did not use the bitset, it squeezed in 3s
Me too. I used bitset to store the dp, but I didn’t use bitwise operations. I put the knapsack part out of the dfs(which I think will be faster), and my solution only executed to 2105ms.
My code
I want to know why I use normal arrat instead of bitset and I passed the test .My solution only executed to 1903ms.
Maybe my English is so bad ,please forgive me.
But I still think the way to achieve the "dynamic" bitset by template is pretty cool!
My code
Maybe it's because I used vector to store the tree. Vector is much slower when $$$n\ge 5\times10^5$$$.
UPD: I changed the way of storing the tree, and it only took 1918ms.
UPD2: Due to the large amount of input,
scanfis very slow. I added input optimizations and the new code only executed to 1201ms.Another optimization:
Since we need to divide a set of integers into two sets, obviously there must be one set that does not contain the maximum element. So we only need to do the knapsack problem for the other elements. It is a bit like dsu on tree.
Here's a stupid solution using std bitset.
Set the bitset to be doubled in size in advance, and then select the smallest bitset that can be used during operation.
https://codeforces.net/contest/1856/submission/217355793
You don't need bitset to get accepted. I think that somehow bitset does not make a big difference?
Custom bitset solution (577ms): 217703571
No bitset solution (701 ms): 217729087
But I mean, theoretically speaking, the solution without bitset is $$$O(n\sqrt{n}\log{}n)$$$, which is supposed to get TLE verdict (compare to $$$O(\frac{n\sqrt{n}\log{}n}{64})$$$ of bitset solution). Maybe it's hard to find a countertest.
Bitsets in authors' solution once again, are they ret...?!?!?!?!?!? (jk)
Make BledDest upset again.
earn BledDest another 50 contribution
Careful Bledest has already started writing his next post!!
Once again, simply use bitset.
may be BledDest has started write a new post :))
This is my solution for 1856E2 - PermuTree (hard version) in testing.
The complexity seems to be $$$O(n\sqrt{n})$$$, however it pass. In fact, it remain one of the fastest solutions.
There are justifications for why it would be fast:
I failed to prove that the complexity is lower than $$$O(n\sqrt{n})$$$, and I failed to produce a test case that would have longer run time. Maybe this is due to a lack of trying, but it would be interesting if anyone can prove or hack it.
UPDATED: system test ended, so you can see my submission 217356778
You can't do that. If your root has one subtree of each $$$1, 2, 3, 4, 5 \dots$$$ sizes, it's complexity is already $$$O(n\sqrt{n})$$$ for solving knapsack just for this.
Btw, I just changed bitset to boolean array in my solution without any additional hacks and time is barely changed at all (421 ms to 452 ms).
That's true, but I was thinking more like, I can't prove the constant factor is low enough that it should pass.
For example, the $$$1, 2, 3, ...$$$ case has a constant factor of like $$$1/3$$$.
Can you please explain the thing "compression algorithm"?
It's an optimization in knapsack problem, where you only care about whether you can construct a sum.
In short, if you have $$$k$$$ copies of $$$x$$$, then you can choose from $$$0$$$ to $$$k$$$ copies of $$$x$$$ in your sum. We will transform $$$k$$$ copies of $$$x$$$ into another set of numbers, such that you can still construct from $$$0$$$ to $$$k$$$ copies of $$$x$$$, but we have less number and faster DP.
The way I did this is that if there are more than $$$2$$$ copies of $$$x$$$, I make $$$x$$$, $$$2x$$$, $$$4x$$$, .... This make it so instead of $$$k$$$ copies of $$$x$$$, I only have $$$O(log(k))$$$ numbers to do DP with.
I don't know where I learned this trick, I might even have came up with it myself, but you can read more about it and knapsack here: https://codeforces.net/blog/entry/98663
Thanks
Am i misunderstand something? If there are are $$$k$$$ copies of $$$x$$$ but $$$k$$$ is a power of $$$2$$$, exmaple $$$k=8$$$, if we make $$$x, 2x, 4x$$$, it can't construct $$$8x$$$, but if we make $$$x, 2x, 4x, 8x$$$, we can make something exceed the limit of k. How we do with it.
for k=8 we can make it as $$$x,2x,4x,x$$$ if last part is small than power of 2. We let it as it is.
E1 hint 4 has wrong formatting
Thanks, fixed.
Problem D using square root decomposition : https://codeforces.net/contest/1856/submission/217356620
C can be done in N^2 by greedy 217325957
I have roughly the same thing except that I got system tested :( 217326485
Take a look at Ticket 17027 from CF Stress for a counter example.
I have this code 217360880 which works on the sample but still gets WA :/
I don't really understand how to use the website though, do I have to pay 15$ to use it ?
Thanks for the nice round and extremely fast editorial (which seems great as it has hints!).
Here is my detailed advice about all the problems:
A nice problem A, easy but there is still a small idea. I think it is exactly what a div2 A should be like! Also, thanks to the authors for putting the for all in bold, I missread the problems for a few minutes :clown:
A great div2 B, there is an idea to have, it is easy to implement and is solvable by most contestants.
The problem by itself is great, I think does the job as a div2 C. I feel a bit dumb for not thinking of binary search and doing some $$$O(n^2)$$$ which ended up getting systemtestED :x
Btw I am curious if anyone can find what's wrong in it: 217326485
I missread the statement (again !) so I can't give my advice as I still haven't thought about the real problem. I'll try to update the comment after solving it.
A very cool problem. I feel like it would be a great educative problem (to help people understanding how a DFS "describes" all paths between pairs of nodes) but it might be a bit too easy for a regular round ? Maybe it is fine as the score was comparable to the score of C
I didn't know about this trick to optimize knapsack DP so I'm happy that I learned something but I feel like it makes the problem about "do you know this trick" (or "did you google how to make knapsack faster"). Again, I think that the problem is great and it might not be bad to have some problems requiring more "tricks" rather than idea.
I thought that E2 was not dp and completely unrelated to E1. Optimization with bitsets never crossed my mind.
.
Video-editorial for problem A&B: https://youtu.be/41aWz1C4QJc
thought would be useful
Can someone please point out what am I missing in my approach of C: 217341446, my answers seem to be off by one from the intended ones.
I'm iterating over all positions from right to left, trying to build a pyramid as high as possible. The first element is bound by its height and height of its neighbor to the right (if there is one). After fixing the starting point I'm going over all elements to the left one by one.
A small example:
n = 4, k = 8, a = [4, 3, 1, 3], the answer in this case is 6The best graphical representation I could come up with in the shortest amount of time.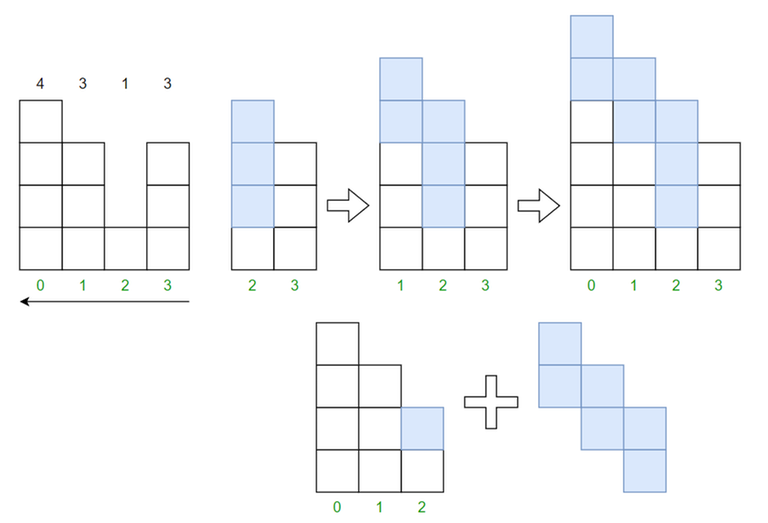
I can either start from the last element and increase the height one by one, or start from i = 2 and then add 2 more layers on top.
For each half-pyramid I'm trying to fill as much blocks as possible on top (amount of operations left divided by the length of a segment).
If someone could come up with a counterexample, I would greatly appreciate that.
UPD.: Turns out it's a classic implementation (skill) issue, basically I was updating the height of the first element in a segment, but I was still calculating heights of new elements based on the initial height, correct submission: 217377033
your logic is to start from some last position and get the max possible encounter till count==k iterating to i>=0 but how the code solves the sample test case 5 , can you explain? there the edgy case is that we have to just make the 1 to 4 and not 6 that is (6,5,4,1,5)-> (6,5,4,4,5)->(6,5,5,4,5)-> (6,6,5,4,5)->(7,6,5,4,5) , my code is giving wrong result for this test case :(. from my code i always iterate like you but always if a[i]<=a[i+1] exists then i make a[i] to be a[i+1]+1, always hence the answer my code gives for this case is 6. metelkov
I have a
prev_sizevariable that tracks the height of the last used element, so starting fromi = 3(zero-based indexing) it is equal to 1, then the next element is 4, which is higher thanprev_size + 1, so I need to increase the height of the whole previous segment (in this case only the first element) by 2, and I have enough operations to do that. Then the rest of the elements form a perfect staircase:6-5-4-3, so I don't need to apply any more operations, but since I have 4 more operations left I can bring this whole segment up by 1:7-6-5-4.Problem C can be easily solved in $$$O(N \log N \log C)$$$.
I forgot the constraint of $$$N$$$ during the contest, so I came up with this solution (217368352).
However, I was too stupid and couldn't implement binary search correctly during the contest.
I finally fixed my solution after the contest. :(
It's possible to speed up this solution to $$$O(N\log N)$$$ by using suffix minimum. My submission: 217428923
why suffix minimum ? a bit elaborate pls the logic your code works on
$$$suf[i]$$$ equals to first such $$$(j >= i)$$$ that satisfies the following expression : $$$a[j] >= mid - (j - i)$$$. To build this array we need slightly modify our expression, $$$a[j] + j - mid >= i$$$. So, the possible $$$i$$$ for each $$$j$$$ lies in segment $$$[1, a[j] + j - mid]$$$. Thus, it will be correct that $$$suf[i]$$$ is applicable for all indices before $$$i$$$ also. It means that $$$suf[i]$$$ will be either: $$$suf[i + 1]$$$, if $$$a[j] + j - mid > i$$$, or minimal $$$(j >= i)$$$ for which satisfies equation $$$a[j] + j - mid = i$$$ (it can be easily handled with pre-building suffix array). If I was unclear, please tell.
when we are building the suff array we are looking for first such (j>=i) why we need to update suff[i] = min ( suff[i] , suff[i+1] ) later ?
E can be solved in $$$n \log^3(n)$$$ using FFT.
Consider the sizes of children of each node — say for a node $$$u$$$, the sizes of child node sub-trees are $$$s_1, s_2, ... , s_c$$$. Then, consider the polynomial $$$(1 + x^{s_1})(1 + x^{s_2})\cdots...(1 + x^{s_c})$$$. The coefficients of this polynomial can be computed in $$$n \log(c) \log(n)$$$. Once we have these coefficients, we will find the closest number to $$$n/2$$$ having non-zero coefficient in the final polynomial. We'll only do this when each child node has size smaller than $$$n/2$$$. Thus, we'll need to do this polynomial computation at most $$$\log(n)$$$ times.
this gives overall time complexity of $$$n \log^2(n) * \log(n)$$$
good luck trying to make this approach pass TL :)
You can remove one log by doing exp(log(1 + x^s1) + log(1 + x^s2) + ...).
An example of a problem using that trick is https://www.codechef.com/JUNE20A/problems/PPARTS
Could you explain this in more detail?
if the max child node size is bigger than n/2，how to deal with the problem？
probably just multiply the max child node num with the rest, since you know it'll be optimal
Can anyone help me debug my solution for C, I am getting wrong answer for some and specific cases and not able to figure it out.
video editorial for problem C binary search solution: https://youtu.be/XSsY00NV0ck
$$$O(nlogn)$$$ is possible for C using binsearch and two pointers method.
Please could you detail a bit more your approach? Thanks by advance.
Binary search over answer, let $$$mid$$$ be number we're checking for whether it is obtainable. For each $$$i$$$ we want to find closest to it's right position $$$p[i]$$$ such that $$$arr[p[i]] \ge mid-(p[i]-i)$$$. It's not that hard to see that if $$$i < j$$$ then $$$p[i] \le p[j]$$$, so we can compute $$$p[]$$$ using two pointers. Now all we have to do is to check whether there exists $$$i$$$ such that number of operations to change segment $$$arr[i .. p[i]-1]$$$ into sequence $$$mid, mid-1, .., mid-(p[i]-1-i)$$$ is $$$\le k$$$. The number of operations to do that is equal to the difference of the sums of both sequences.
thanks!
Here I am adding an easy to understand code running in O(N log(A + N)) where A is maximum element in array https://codeforces.net/contest/1856/submission/268560482
For E1 partition a set into two subsets such that the difference of subset sums is minimum
In problem E2, does the condition in Hint 2 ( If there is a subtree that is bigger than the sum of the sizes of the other subtrees, you don't have to do knapsack) help in improving the time complexity, or is merely a heurestic? I was able to figure out the Nroot(N) solution but did'nt know about this and the bitset optimisation :(
Assuming we're using bitsets of size not larger than twice the size of subtree, the total size of used bitsets will not exceed $$$O(nlogn)$$$ if we consider the idea in Hint 2, otherwise we need $$$O(n^2)$$$ (if we use the same bitset for another dp then we count the space used again). This can be proven by considering HLD of the tree or just small to large argument.
Oh thanks a lot for the explanation. Interesting question ngl
It helps because whenever you have to compute it for a subtree of size N, you'll split it into subtrees that sum up to less than N and each individual subtree is of size less than N/2. I think that we can prove a bound like T(N) = O(N^1.5) + 2*T(N/2) which you can use https://www.nayuki.io/page/master-theorem-solver-javascript to calculate the result.
Yeah got it, thanks a lot for the explanation and the tool 👍
Got bit confused by B during the contest and wasted some time before arriving at really intuitive solution -
Reduce all the elements which are greater than one to 1. Now, for every element x, we have to add
x - 1to leftover elements. We can get the sum over all such x. Let's call it add. Now, we can count all the ones in the array so that we distribute the sum to those ones. In case ouradd >= countOfOnes, we can easily increment all the ones and hence a new value. In case add is less, there would atleast be one1which can't be changed. Answer would beNoin that case. And obviously ifn = 1, we can't change the value so answer is No.In problem $$$E1$$$ I tried to do something similar to inorder traversal.
and made $$$p_i$$$ equal to the visit order of node $$$i$$$.
so by doing that, every node that is $$$lca$$$ to at least two nodes will be counted in the answer $$$number \space of \space nodes \space to \space its \space left$$$ $$$*$$$ $$$number \space of \space nodes \space to \space its \space right$$$.
can someone explain why is this wrong.
my submission 217355939.
Consider the case where the sizes of children of some node are 1 1 2 2 respectively. Then your solution will count (1+1)*(2+2) = 8 triplets, where optimal solution in this case is to divide the children equally: (1+2)*(1+2) = 9 triplets.
I had the same idea as you at first, and implement it at once. After getting wa on 7, I realized that there was a problem.
so how to define the visit order on multi-pronged tree? We don't know which son is the first and which is the last. divide these sons seems impossible.
the right solution is to divide sons into two seperated sets, and make the subtraction of two sets minimum.
for example, if the node sizes are $$$1,2,3,4$$$, your solution may count $$$(1+2)\times(3+4)=21$$$, but optimal solution is $$$(1+4)\times(2+3)=25$$$, which has the minimum subtraction $$$(1+4)-(2+3)=0$$$ in this case.
Can you explain how we ensure that in the optimal solution, the sons themselves are not going to be subdivided?
As in, why are we not considering possibilities like $$$(1 + 2 + 2) \times (2 + 3)$$$. (I know unoptimal in this case, asking in general).
You cannot subdivide the sons. After the division we add all the pairs of form $$$(a, b)$$$ where $$$a$$$ is an item from first group and $$$b$$$ from the second. If we were to split sons $$$v, u$$$ from the same subtree into two groups, then we would also count $$$(v, u)$$$, but we should notice that their lca isn't the root of our current subtree, so we cannot count right now.
Sorry if I wasn't clear before, but this is not what I wanted to ask.
The Hint 1 of E2 says -
For every $$$lca(u,v)$$$ we actually need to do Knapsack on the subtree sizes.
Could you tell me why this is true? In the solution to E1, this optimization is not used. The solution has iterated over divided subtrees also.
It does use this optimization. In dfs we're pushing sons' subtree sizes to vector $$$a$$$ which we later use to do knapsack.
I still don't get it. Why are we defining the variables $$$0 \leq b_i \leq s_i$$$ if we are not considering the subtrees being split into group of $$$b_i$$$ and $$$s_i - b_i$$$ themselves?
If I am not understanding it wrong, in E2 we need to use that $$$b_i = s_i$$$ (or 0) in the optimal solution right?
Where does that come from?
I don't get where are you getting $$$b_i$$$ from. Both E1 and E2 use the original sons' subtrees sizes.
I am talking about the $$$b_i$$$ s from Tutorial of E1
I've added the tutorial for E2, I think the answer to your original question can be found there.
This tutorial is so messy that I'm not even going to bother reading it. Easier way to understand this goes as follows: Suppose we're at vertex $$$x$$$ and we want to find maximum number of pairs $$$(v,u)$$$ such that $$$a_v < a_{lca(v,u)} < a_u$$$ and $$$lca(v,u) = x$$$. Let $$$S_1$$$ be set of all vertices $$$v$$$ in subtree of $$$x$$$ such that $$$a_v < a_{lca(v,u)}$$$, analogically for $$$S_2$$$. Let $$$y$$$ be some son of $$$x$$$ and $$$a, b$$$ some vertices in subtree of $$$y$$$. We will prove that it does not make sense to split $$$a$$$ and $$$b$$$ into separate sets. Let $$$s_1$$$ be the size of $$$S_1$$$ without vertices from subtree $$$y$$$, same for $$$s_2$$$. If we put them in separate sets, then their contribution to the answer at $$$x$$$ will be $$$s_1+s_2$$$, where if we were to put them in the same set, then it would be either $$$2s_1$$$ or $$$2s_2$$$, so we should pick the greater one. It is easy to show that $$$s_1+s_2 \le max(2s_1, 2s_2)$$$. So it is always optimal to place all vertices from the same subtree in one of those sets.
Can someone explain how solving knapsack in $$$O(s*\sqrt{s})$$$ leads to solving E2 in $$$O(n*\sqrt{n})$$$?
During the contest, I thought it was $$$O(n*\log{n}*\sqrt{n})$$$. For a vertice, the sum of weights is the sum of sizes of light children which is bounded by $$$O(n*\log{n})$$$ for the whole tree. The number of items on a vertice is bounded by $$$O(\sqrt{subtree size})$$$.
First, prove that this complexity leads to $$$n \cdot (\sqrt{n} + \sqrt{\frac{n}{2}} + \sqrt{\frac{n}{4}} + \sqrt{\frac{n}{8}} + \dots)$$$.
Then we can observe that $$$\sqrt{n} + \sqrt{\frac{n}{4}} + \sqrt{\frac{n}{16}} + \dots = \sqrt{n} + \frac{\sqrt{n}}{2} + \frac{\sqrt{n}}{4} + \dots < 2 \cdot \sqrt{n}$$$.
And the same thing we can do with even terms sum ($$$\sqrt{\frac{n}{2}} + \sqrt{\frac{n}{8}} + \sqrt{\frac{n}{32}} + \dots$$$).
can you elaborate how complexity lead to the first equation? .
Let's say the vertex has level $$$i$$$ if we calculate the knapsack in this vertex and in exactly $$$i$$$ of its ancestors. Because we calculate knapsack only in light child, a subtree size of an $$$i$$$ level root $$$\le \frac{n}{2^i}$$$. And, by definition, subtrees with the same level roots can't be nested. Therefore, the sum of all $$$i$$$ level vertices subtrees $$$\le n$$$ and so the knapsack calculation for all of them together $$$\le n \cdot \sqrt{\frac{n}{2^i}}$$$. This leads to the first equation.
I updated the provided solution for Problem C Because those portion of the code was creating Confusion.
...
Thanks! By the way, you should put the code in a spoiler, right now it's taking up quite a lot of space.
"If there is a very subtree that is bigger than the sum of the sizes of the other subtrees, you don't have to do knapsack."
why does it speedup solution so much ? I tried to solve it without it, but even in the Gym with 15s time limit it gave TLE
is it something similar with small to large ?
Hey! I asked this question few comments ago, linking it here for your reference :) Link to Comment
thank you! I didn't notice that
For E1, I iterated on all the lca(u,v). After fixing node, let $$$c_{1},c_{2},c_{3}... c_{k}$$$ be the sizes of subtree rooted at the children of node. Then we divide them into two sets $$$S_{1}, S_{2}$$$ and for that node the answer will be the maximum of the Sum($$$S_{1}$$$)*Sum($$$S_{2}$$$) over all such divisions. This is $$$O(n^{2})$$$.
How can I optimize it for E2.
I used an approach for problem D that only uses $$$3 \cdot n^2$$$ coins. The idea is similar to the editorial, except you just keep a list of potential candidates for the maximum (initially set to all $$$n$$$ positions). Then you always greedily compare the two closest candidates and remove one of them.
Code is 217298513 as well as a YouTube video explanation here.
Note that in the video I only prove $$$\frac{\pi^2}{3} \cdot n^2 \approx 3.29 \cdot n^2$$$, but you can actually prove that it's $$$3 \cdot n^2$$$.
bitset in author's solution. why??????
Very cool task E2, thank you!
I encountered weird bug while solving E2 and I can't understand what is wrong. This 217392127 passes freely, whereas this one 217392094 gets RE. Notice that the only difference between those codes is one commented out line (which is some bitset operation); the line is inside else statement, which I intentionally made to never execute. The RE occurs on line (shaped) graph (notice that on such graph DFS always returns before running knapsack part). Any ideas why one solution works and the other doesn't?
It seems that the time complexity of the official solution for E2 is $$$O(\frac{n\sqrt(n)\log n}{\omega})$$$, as same as My submission's.Why I got TLE?
You don't change
khere, so it is always equal to $$$1$$$.Thanks I'm too careless……
Can Somebody suggest me free resources to reach specialist
Could someone please teach me how to prove complexity in E2?
E2 uses O(n√n) knapsack with bitset optimization, and small to large trick, so u can read about them somewhere
These are pretty good problems.D,E1 and E2 are challenging
Good problem C!But I use an $$$O(n^3)$$$ way to solve it.
This is my code:
Cool. But unlucky for u it's too slow
But It runs just 202ms,in my opinion,it isn't too slow.
This is the link.
I think maybe the reason is that the datas arenot to limit your solution.Otherwise,your solution doesn't run fully.
the "dynamic" subset using
std::bitsettrick in the solution of is really cool!Isn't the dp part in E1 has time complexity $$$n*sum$$$ which is $$$O(n^{3})$$$, Can someone explain how it's $$$n^{2}$$$ ?
Let the number of children of the $$${ith}$$$ node be denoted as $$${n_i}$$$. Now, $$$\sum_{i=1}^{i=n} {n_i = n - 1}$$$. This is because every child has only one parent, which further means that every node will only be counted once in any of $$${n_i \forall i \in [1, n]}$$$.
Now, the dp in question will basically run (for every node $$${i}$$$) on $$${n_i}$$$ nodes. And as it will run for every node $$${i}$$$, we get total time taken = $$$\sum_{i=1}^{i=n} {O({n_i}*sum)}$$$ = $$${O(n * sum)}$$$ = $$${O({n^2})}$$$
You can read the #7 of this blog
Has a similar problem to C occured before in a contest. I couldn't think of how to aplly binary search in this question.
Can someone explain me the $$$\text{dp}$$$ states in $$$\text{E1}$$$?
It seems currently the Tutorial is not available for $$$\text{E1}$$$ and $$$\text{E2}$$$.
In B problem, I replaced 1 with 2 and all the other values I replaced with 1(the last element will be set in a way such that the sum remains the same), why doesn't this work?
There are cases when you cannot replace all 1's with 2. Are you handling that?
I just understood the solution(by proving it on pen and paper), so now I understand where I went wrong. Thanks :)
Finally Specialist...!!! Yayy
In E1, it seems obviously that all of the values allocated to a specific subtree are larger or smaller than the value of LCA. But by allocating both larger numbers and smaller numbers to a subtree, the product will become higher and we need to exclude the pairs in this subtree. Can anyone proof that the final answer won't become larger? Thanks a lot.
I'm wondering the same thing, however in E1 the model solution uses DP where they try all distributions.
Thanks, I didn't notice that.
But in this code, I did not enumerate the number of large and small numbers assigned to the subtree, and I did not consider the situation that the large and small numbers are in the same subtree when counting the results, and I got Accepted.
So is this the right way to solve the problem or is the input set not strong enough?
No, it's right, E2 uses this. I don't think you are the only one who didn't bother proving it before submitting.
Here for someone to prove it later, I am also stuck trying to proof this claim.
Assume the LCA is node $$$x$$$ which has $$$n$$$ children and value $$$x_v$$$, and you have assigned $$$a_i$$$ nodes of the $$$i^{th}$$$ child subtree values smaller than $$$x_v$$$ and assigned $$$b_i$$$ nodes values larger than $$$x_v$$$, the contribution of the $$$i^{th}$$$ subtree will be $$$a_i\cdot \sum_{j=1}^{j=n}{b_j}+b_i\cdot \sum_{j=1}^{j=n}{a_j}$$$ where $$$j\neq i$$$.
Now if we decide to merge the part which is multiplied by $$$min(\sum_{j=1}^{j=n}{a_j}, \sum_{j=1}^{j=n}{b_j})$$$ with the other part, this will affect the contribution by: $$$ChoosenPart\cdot (max(\sum_{j=1}^{j=n}{a_j}, \sum_{j=1}^{j=n}{b_j}) - min(\sum_{j=1}^{j=n}{a_j}, \sum_{j=1}^{j=n}{b_j}))$$$, which means contribution didn't decrease.
If I understand correctly, when you fix other parts and change the distribution of values in a subtree, the contribution of that subtree will indeed reach the maximum or minimum value when it comes to all small or large numbers. However, this contribution is not independent, as it may reduce the contribution of other subtrees.
We can start the proof from the upper subtrees, this will not affect the lower subtrees as any set of values allocated to the lower subtrees can be arranged appropriately to achieve some arrangement. Now in the lower subtrees the change will not affect the upper subtrees as the values in any subtree are all less or larger than any upper level LCA.
It is correct for contributions between different levels to be independent of each other, but what I want to say is that the contributions of subtrees within the same level will affect each other. For example, if you change the
a_iof a subtree to get a higher contribution, it will feedback on the contribution of another subtreejin the same level, as the its contribution will suma_i.Note that when I calculated the contribution of the $$$i^{th}$$$ subtree, I calculated its whole contribution (of both $$$a_i$$$ and $$$b_i$$$), so the contributions of other subtrees within the same level should not consider $$$i$$$ at all.
DP solution for problem C incase anybody needs it. I have used binary search to finally filter out the value. Incase any further explanation is required, feel free to ask, I'll try my best to explain
tutor for E1/E2 when?
Added tutorial for E1.
For problem E2, I think my code works the same as the one in the editorial but it keeps on getting TLE on testcase 5. Can anyone help me? 217457280
The problem with your code is that you're using maxsize bitset for every dp. The way around this is to use templates to generate solve functions with bitsets with sizes of powers of 2. This trick is used in editorial solution.
Thank you so much for your help!
Why does bitset with maxn take much longer even though I'm not using all of the bits for every calculation?
Because you're using whole bitset while performing shifts.
Oh I see thank you
I have solved $$$E1$$$ using a different DP, but I spent some time to understand what the DP used in the editorial's solution means, and here is what I got (note that I used some variable names from the code):
For a node $$$v$$$ with $$$n$$$ children, we make $$$n$$$ iterations, in the $$$j^{th}$$$ iteration we add the $$$j^{th}$$$ child subtree, which has a size $$$x$$$. $$$cs$$$ is the sum of sizes of the previous subtrees excluding the $$$j^{th}$$$.
In the $$$j^{th}$$$ iteration, we calculate $$$dp[i]$$$ which is, using the first $$$j$$$ subtrees, $$$dp[i]$$$ is the maximum number of good pairs having LCA $$$v$$$, if we have $$$i$$$ nodes with values less than $$$v$$$'s value, where $$$pr$$$ from them are chosen from $$$cs$$$.
Here's my solution for E2 without using any bitset optimization or any compression, just using the fact that there are atmost around sqrt(2*subtree_sum) distinct numbers which sum upto subtree_sum. I am wondering how this solution passes in just 1310 ms.
Problem E2:
Let $$$d_1,d_2,…,d_p$$$ be the sizes of the subtrees of vertices in $$$L_k$$$ . Then we need to maximize the value of: $$$d_1\sqrt{d_1}+d_2\sqrt{d_2}+…+d_p\sqrt{d_p}$$$ over all $$$d_1,d_2,…,d_p$$$ such that $$$1≤d_i≤\frac{n}{2 ^ k}$$$ and $$$d_1+…+d_n≤n$$$ .
Can't we just prove that: $$$d_1\sqrt{d_1}+d_2\sqrt{d_2}+…+d_p\sqrt{d_p} \leq d_1\sqrt{\frac{n}{2 ^ k}}+d_2\sqrt{\frac{n}{2 ^ k}}+…+d_p\sqrt{\frac{n}{2 ^ k}} = \sqrt{\frac{n}{2 ^ k}} (d_1 + d_2 + ... + d_p) \leq \sqrt{\frac{n}{2 ^ k}}\cdot n = \sqrt{t} \cdot n$$$
Seems correct, I don't know how I missed that...
why does a code with lambda expressions is taking more space? 218007219 and 218004946 are exactly same codes but in one of them I used lambda function instead of ordinary function and it gives me stack overflow for large input. All I know is after function is executed it is cleared from stack, same happens with lambdas. Moreover the code runs for O(n sqrt(n)) complexity !!
Has anyone managed to solve E2 with recursive dfs?
218054678
I eventually solved it without dfs, but I wonder if dfs always stackoverflows for graph problems with n=1e6?
I do not understand why i get TLE on problem E2. Nothing seems wrong.
Here is my code: 218196327
You can't use a bitset of length $$$n$$$ for every vertex, it makes the solution run in $$$O(\frac{n^2}{w})$$$. For example, on a tree with a lot of vertices that have three subtrees of sizes 2, 3, and 3.
Why is dp[i][B] the array's m⋅(Sm+1) values taken into account of the time complexity of the problem E1?
Because allocating the $$$dp$$$ array (or if you are using a global array, setting some values to zero) takes time, though in this case, it doesn't affect the complexity.
Intuitive DP for C:
Let $$$dp_{i, j, k}$$$ represent if it is possible to achieve value $$$j$$$ at index $$$i$$$ using $$$k$$$ increases (this is separate from $$$k$$$ as defined in the problem). Based on the problem statement, for $$$a_i$$$ to increase to $$$j$$$, $$$a_{i+1} \geq j-1$$$. And to increase $$$a_i$$$ to $$$j$$$, you must use $$$j-a_i$$$ increases. This gives the recurrence:
For each individual $$$i$$$, $$$j$$$ can be binary searched. It's easy to see that the recursion depth is at most $$$n$$$, so the total complexity is quadratic and an insignificant log factor from binary searching.
An O(n) solution to C: https://codeforces.net/contest/1856/submission/229939313
For any $$$i$$$, assume $$$i$$$ is the highest. Then $$$a[i+j]=a[i]-j$$$ for $$$i\le i+j\le r_i$$$. If it's possible to convert both $$$(a,b)$$$ and $$$(c,d)$$$, and $$$a\le c\le d\le b$$$, then it's always better to choose $$$(a,b)$$$. So you only care about values of $$$r_i>\max(r_{i-1})$$$, so you can use two pointers.
c c 2c problem c c. p3
$$$f(i,y)=+∞$$$ for $$$i=n$$$ and all $$$y>a_i$$$. What does the $$$y>a_i$$$ mean in this case? Is $$$y>a_i$$$ not covered in the previous case?
in the question c , i used dp with binary search having a complexity n*n*log(k) but it is showing TLE .can someone told me why is it happening????
my code is below
https://codeforces.net/contest/1856/submission/264697384
Nice editorial, the explaination for E1 is very good. Props to the editorialist