Hello, Codeforces!
I recently came across a data structure that I find quite interesting: the sparse set. It functions similarly to a bitset and supports all its operations but has some quirks and useful features of its own. Particularly, unlike almost every other data structure, it does not need to be initialised at all before it can be used! Naturally, that also means that its data can be reset in $$$O(1)$$$ time, as opposed to the $$$O(n)$$$ time expected of regular bitsets. It also has the added benefit that traversing its elements takes time proportional to the number of elements rather than the size of the data structure, making the operation more efficient for sparse bitsets. However, note that it is likely less efficient in terms of its memory usage (still $$$O(n)$$$ but ~64× larger constant) and constant time factor.
Introduction
The sparse set consists simply of two integer arrays (which I'll call $$$d$$$ and $$$s$$$) and a size variable $$$n$$$, satisfying the following class invariants:
- Invariant 1: $$$d[0..(n-1)]$$$ (inclusive) stores the elements of the bitset;
- Invariant 2: If $$$e$$$ is an element of the bitset, then $$$s[e]$$$ stores its index in the $$$d$$$ array.
In most literature covering this data structure, the arrays $$$d$$$ and $$$s$$$ are called the 'dense' and the 'sparse' arrays, respectively.
For any array element not mentioned above, its value can be anything without affecting the function of the data structure.
A typical sparse set might look like this (asterisk denotes terms that can be anything): 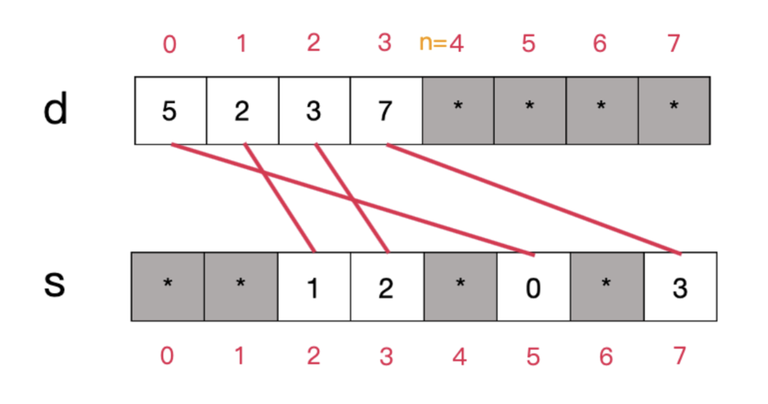
The red lines indicate the connections between the elements in $$$d$$$ and $$$s$$$. It can be shown that, for all indices $$$i$$$ in the range $$$[0, n-1]$$$, the constraint $$$d[s[d[i]]] = d[i]$$$ is satisfied.
In C++ code, the data structure can be represented as follows:
template <int N>
struct sparse_set {
int n;
int d[N], s[N];
};
Note that, in this article, we would use $$$N$$$ to denote the size of the data structure itself (and thus, the set of elements allowed is $$${0, 1, \ldots, N-1}$$$), and $$$n$$$ to denote the number of elements currently stored.
Important implementation detail: if you are using C, C++, or Rust, you still have to initialise this data structure in its constructor since accessing an uninitialised element does not return an unspecified value; it is undefined behaviour and can introduce bugs elsewhere in your program. You don't have to do this when resetting the data structure, however.
Lookup
- Precondition: $$$idx$$$ is a value between $$$0$$$ and $$$N-1$$$;
- Postcondition: the data structure is unmodified, and $$$idx$$$'s presence in the bitset is returned.
- Time cost: $$$O(1)$$$
Surely, since $$$s[i]$$$ stores the position of element $$$i$$$ in $$$d$$$, I can simply check if $$$s[i]$$$ is between $$$0$$$ and $$$n-1$$$ to determine whether $$$i$$$ is in the bitset, right?
// Intentionally incorrect code!
template <int N>
bool sparse_set<N>::test(int idx) const {
return s[idx] >= 0 && s[idx] < n;
}
Not really… it is entirely possible that $$$i$$$ is not in the set, yet $$$s[i]$$$ has a 'valid' value between $$$0$$$ and $$$n-1$$$ since the data structure specifies no guarantees for values of $$$s[i]$$$ where $$$i$$$ is not an element; therefore false positives might arise. We have to check if the value of $$$d[s[i]]$$$ links back to the correct value of $$$i$$$.
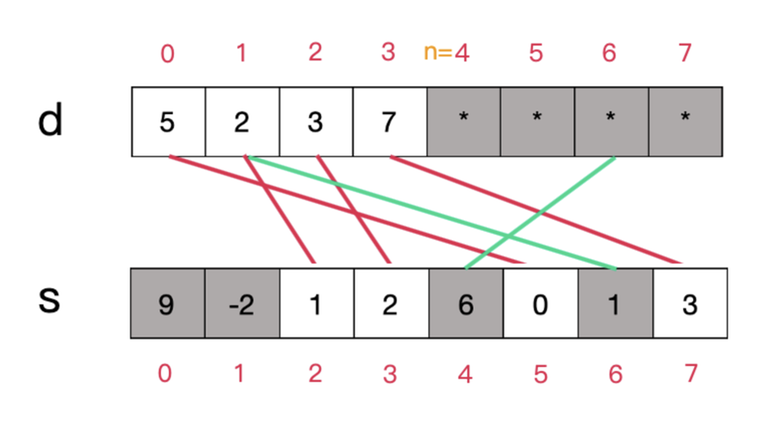
Here, 6 isn't actually stored in the data structure, but $$$s[6]$$$ happened to be a 'correct' index, misleading our erroneous algorithm to think that it is.
The correct implementation of the lookup operation would look something like this:
template <int N>
bool sparse_set<N>::test(int idx) const {
return s[idx] >= 0 && s[idx] < n && d[s[idx]] == idx;
}
Insertion
- Precondition: $$$idx$$$ is an integer between $$$0$$$ and $$$N-1$$$.
- Postcondition: $$$idx$$$ is inserted into the data structure if and only if it wasn't already present.
- Time cost: $$$O(1)$$$
Just like normal bitsets, our implementation does not allow duplicate elements. Therefore, we have to check whether the element is present before inserting. Inserting an element is a rather simple operation: if the element is not already present, we push its value onto the $$$d$$$ array, update $$$s[idx]$$$ to the correct value, and then increment the value of $$$n$$$ by $$$1$$$.
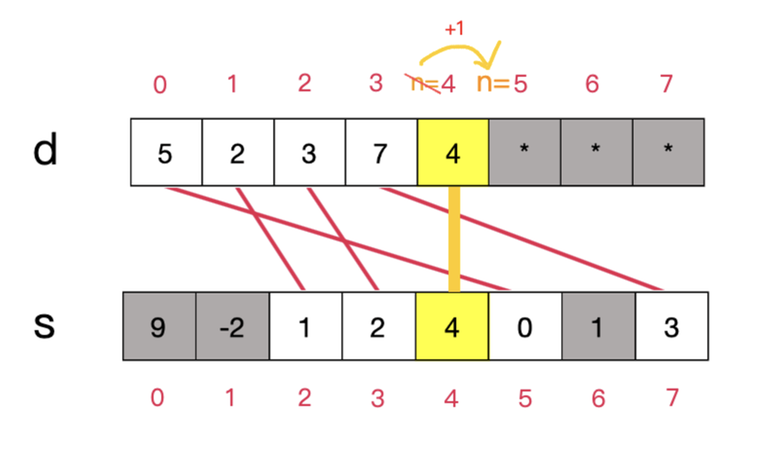
The code to do this would look a bit like this:
template <int N>
void sparse_set<N>::set(int idx) {
if (test(idx)) { return; }
d[n] = idx;
s[idx] = n;
n++;
}
Deletion
- Precondition: $$$idx$$$ is an index between $$$0$$$ and $$$N-1$$$.
- Postcondition: if $$$idx$$$ was inside the set, it is now removed.
- Time cost: $$$O(1)$$$.
As the inverse operation of insertion, deletion is slightly more complex to implement than insertion but is nevertheless still rather straightforward. The central idea is to swap the last element with the element to be deleted in the $$$d$$$ array, then update the corresponding values in $$$s$$$ accordingly.
Basic procedure:
- We want to make $$$idx$$$ the new position for our last element, therefore change $$$s[d[n-1]]$$$ to $$$s[idx]$$$.
- Overwrite $$$d[s[idx]]$$$ with the value of $$$d[n-1]$$$.
- Decrement $$$n$$$ by $$$1$$$.
- No need to modify $$$s[idx]$$$ since the class invariant doesn't care about $$$s[e]$$$ for deleted elements $$$e$$$.
The diagram for doing the above operations would look a bit like this: 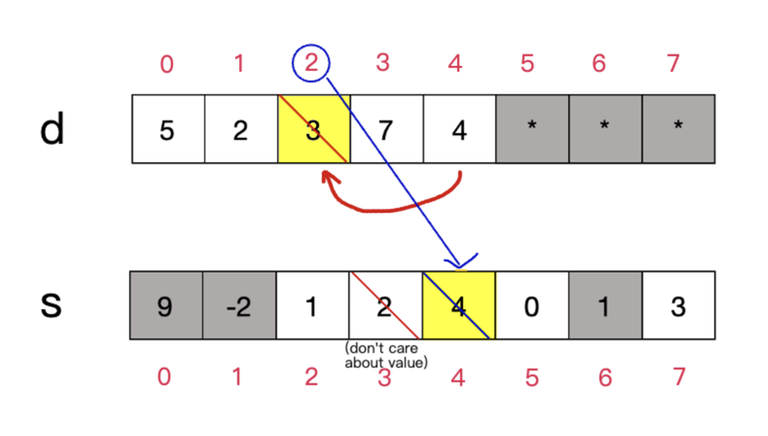
Note that the above procedure still works when the element being deleted is the last element in the $$$d$$$ array, albeit with extra steps. However, since deletions to the last element are rare, it is not worth adding a branch to check for this condition.
Therefore, the code for this operation would look as follows:
template <int N>
void sparse_set<N>::reset(int idx) {
if (!test(idx)) { return; }
d[s[idx]] = d[n-1];
s[d[n-1]] = s[idx];
n--;
}
Clearance
- Precondition: None
- Postcondition: the bitset is cleared. Before modifications,
.get(i)returns false for all valid $$$i$$$. - Time cost: $$$O(1)$$$
Out of all the operations that the sparse set supports, this is arguably the most powerful, taking only $$$O(1)$$$ time to compute, with an extremely simple implementation.

This is literally everything that has to be done :)
template <int N>
void sparse_set<N>::reset() {
n = 0;
}
Iteration
- Precondition: None
- Postcondition: Iterates through the elements of the bitset.
- Time cost: $$$O(n)$$$ (note: $$$n$$$ is the number of elements present. This is different from $$$O(N)$$$ where $$$N$$$ is the size of the container)
This is another operation where the sparse set is better than the classic bitset. Rather than iterating bit-by-bit and checking whether each element is present, we can simply iterate through $$$d[0..(n-1)]$$$ (inclusive) to obtain the list of elements present in the bitset.
As an added bonus, if no deletion operation has been conducted since the last initialisation/clearance, the elements in $$$d[0..(n-1)]$$$ will be in the order that they are added, with the least recently added item in $$$d[0]$$$ and the most recent in $$$d[n-1]$$$, just like a vector.
Full Implementation
The following is a C++ template implementation of the sparse set that I have written. It tries to implement all functionalities of a vanilla C++ bitset.
Some implementation details:
- The type of data this implementation of the sparse set stores is
std::size_t, just like the STL bitset. - Like the STL bitset, using
[]to access and modify elements is supported. The semantics are the same as a STL bitset. test,set,reset, andflipall throwstd::out_of_rangeif the parameter is greater than or equal to $$$N$$$. However, using[]to access elements with out-of-range indices results in undefined behaviour.- Iterators are supported and iterate through all elements in the set. The values they point to are immutable.
- This also means you can use a range-for loop to access all elements of a sparse set.
Conclusion
While the sparse set data structure is rather obscure and almost never used in competitive programming, I think it can be useful in quite a few scenarios. In particular, it can be used as a more performant and hack-resistant version of std::set and std::unordered_set when the only type of data that needs to be stored is small integers. I believe that many of its applications already have alternatives in the STL, however.
So, the above is just a little data structure that I would like to share with you all. If you have any feedback regarding the content or the format (by the way, I really need a better method of creating these diagrams), please kindly leave it in the comments below. Thank you so much for reading all the way here!











For people who not interested in this blog, here's a more generalized spam method.
It uses less memory than the ds mentioned in the blog and is faster and easier to understand.
It's really hard for me to understand why invented this spread set.
Because with the idea from the blog you can also iterate through the values.
omg bitset
can someone link a problem where O(1) clear is needed?
There probably won't be any problems specifically utilizing sparse set's $$$O(1)$$$ clear for better complexity, because for any data structure, you could always just keep track of everything you did to the data structure in a stack and undo all of it, so it will never exceed the complexity of putting the data in there in the first place via normal operations, which gives $$$O(1)$$$ amortized time for clear.
Also this "amortized" is actually strictly $$$O(1)$$$, in the sense that you're never "overspending" your complexity, since every normal operation will cause at most $$$1$$$ clear operation in the end.
hmm amortization falls apart with persistence
This is not a bitset, because is does not shrink the size of data used per possible element to one bit and does not allow to use mass operations $$$w$$$ times faster.
This is not
std::setbecause it does not allow you to iterate elements in sorted order and does not havelower_boundandupper_bound.Ability to have $$$\mathcal{O}(1)$$$ clear is really obscure and most likely is never really required. Because, as you've mentioned, in manually-managed-memory languages memory still has to be initialized at least once. After that number of deletions cannot exceed number of insertions, so it cannot make amortized complexity worse.
However this is very interesting and I see a combination of two ideas in this data structure.
First one. You can achieve $$$\mathcal{O}(1)$$$ deletion from
std::vectorif you do not care about the order of elements. It can be done by swapping erasing element to last position and usingpop_back:I discovered this trick when I wanted to delete some edges from the graph while traversing it. Graph was stored in form of adjacency lists
vector<vector<int>> graph. I was worried to not break the remaining data in the lists and be able to delete while iterating through each element exactly once in arbitrary order. It allowed me to keep vectors and to not introduce some extra linear passes.Second one. Backing up a data structure which does not allow for iteration (or iteration is complicated, or not fast) with extra linear dense container, that will be used to bookkeep elements and iterate them.
Currently your data structure is some fancy version of count sort data structure (but limited to no duplicates). But it is also very similar to structure named Linked Hash Map and here is the way how to turn it into:
In order to extend keys to arbitrary hashable types, we will take hash of the key and use it (modulo number of buckets) as the index of bucket to store the value (adding some anti-collision techniques).
This is basicly it, we can have a working hash map and a list of keys that will allow us to iterate it.
But actual Linked Hash Map instead of using some kind of array list, use linked list instead. This allows them to avoid swapping elements and preserve elements in the order of insertion while keeping all insert/erase/lookup operations $$$\mathcal{O}(1)$$$.
UPD. Worth mentioning. This also allows Linked Hash Map to iterate all elements linear to number of elements, but not to number of buckets. Usually this does not matter as
load_factoris not very small and1 / load_factoris still a constant, but it can make a difference if you will decide to change it or to implement your own hash map.Thank you for your insights. Indeed, the $$$O(1)$$$ clear time cost is unlikely to be very useful since, as earlier commenters have pointed out, most containers already have an amortised $$$O(1)$$$ time for clearing. I only mentioned it since it is a rare case of a data structure providing true $$$O(1)$$$ clearance.
For your first idea, I think one advantage the sparse set has over vectors is that you don't need to have access to the index of the element you wish to delete; only having its value would've been enough. One can use a hash map together with a vector to circumvent this, however.
Your second idea does give me some inspiration on how to use this data structure. I believe that it can be useful as an alternative to a linked hash map when the order of the elements does not matter since it likely takes up less memory and is more cache-friendly. Maybe it can also be used to augment a
std::setto provide $$$O(1)$$$ lookups and $$$O(n)$$$ non-ordered iteration?Probably there are some scenarios where this data structure can outperform standard approaches to the point where is becomes worth introducing. But that should be very specific scenarios:
You have to care about performance. Because otherwise you can just do anything by storing a bunch of sets and maps with all kinds of additional information.
You have to care about data structure iteration speed. Because otherwise you better go with bitset, array of booleans or a custom hash map that does not maintain extra stuff.
You only care about complete collection scans or want arbitrary order, because after you delete an element order of elements is changed and old iterator in the middle of collection no longer guaranteed to scan all elements (unless deletion is tied to this iterator).
You have to care about non-amortized complexities or about additional memory very strictly. Because otherwise you can just use "deleted" marks for the elements instead of real deletion and clean them all up on the next scan.
I also doubt about cache-friendliness, because iterating over external list where every element points to some arbitrary part of main array can easily lead to unpredictable memory jumps. From the perspective of caches straight up scanning through the main sparse array of buckets will technically be
1 / load_factortimes slower but is way more likely to be cache-friendly as you are just scanning memory consequently, especially if done with bitsets.