This is not a problem from any online judge, but for a project I am working on.
There is an ellipse and a list of points. The task is to score the list with a number between $$$0$$$ and $$$1$$$. A score of $$$1$$$ means that the list of points forms a perfect ellipse. A list forms a perfect ellipse when:
All the points in the list lie on the circumference of the ellipse.
The points are evenly spaced (distributed evenly) across the circumference.
The expected time complexity is less than $$$O(N^3)$$$, not strictly necessary. $$$N$$$ being the number of points in the list.
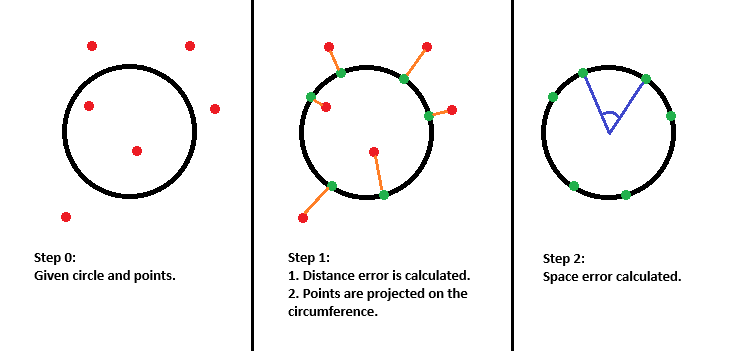
If you want some inspiration, I have attempted the same problem but checked matching with circles and polygons. I am explaining how I did it for the circle.
You can see how the same method will work for regular polygons. For irregular (closed) polygons, I have a more sophisticated but similar way. The closed polygon method can work for ellipses (since an ellipse is actually a closed polygon with many small lines), but I am looking for a more natural solution for ellipses.











Auto comment: topic has been updated by sahaun (previous revision, new revision, compare).
You can do shear transformation (which is 2x2 matrix) to convert an ellipse into circle. You can apply this transformation to input list of points also. Then, calculate the score for circle with transformed points as you would do for a circle.