This problem can be solved in many ways. But I found no online technique editorial which I followed to solve (using binary lifting) this problem. That's why I decided to write this solution blog where I'll discuss the solution from scratch, so that anyone who didn't solve the problem yet, can take help from this blog. Let's dive into the solution.
Update: Here is the solution involving no data structures and just using only suffix sums and binary search.
Pre-requisites: Binary lifting, finding the index of next greater element for all indices using monotonic stack.
How to approach the solution
Let's first think about the naive $$$O(nq)$$$ solution. For each query of range $$$[l,r]$$$, the answer is $$$\sum_{i=l}^r \textrm{max}_{j=l}^i(a_j) - a_i$$$. We can calculate it using a loop within a query easily. By keeping track of the prefix maximum of range $$$[l, i]$$$, we can find out the $$$\textrm{max}_{j=l}^r(a_j)$$$.
Here see that, the equation of the answer of a query can be rewritten as, $$$\sum_{i=l}^r \textrm{max}_{j=l}^i(a_j) - \sum_{i=l}^r a_i$$$. The main challenge here is to find out the first part ($$$\sum_{i=l}^r\textrm{max}_{j=l}^i a_j$$$) fast.
How to solve $$$\sum_{i=l}^r\textrm{max}_{j=l}^i(a_j)$$$ faster
If you observe closely, we can divide the query range $$$[l,r]$$$ into several sub-ranges in such a way that each element of a range will contribute the same value to the sum. For example, the array $$$[4,3,2,5,2,8,10,10]$$$ can be divided into $$$[4,3,2],[5,2],[8],[10,10]$$$ sub-ranges. Notice, that each element of each subrange will contribute a value equal to the first element of that sub-range. So the contribution of a sub-range to a sum can be calculated as $$$\textit{first element}\times\textit{size of the sub-range}$$$. In this example, the $$$1^{st}$$$ sub-range contributes $$$12$$$, $$$2^{nd}$$$ sub-range contributes $$$10$$$, $$$3^{rd}$$$ contributes $$$8$$$ and $$$4^{th}$$$ contributes $$$20$$$. So, the value of $$$\sum_{i=l}^r\textrm{max}_{j=l}^i(a_j)=50$$$.
Let's define a terminology for the rest of the explanation $$$nextGreater(i)=\textit{next greater element's index of }a_i$$$. Formally, $$$nextGreater(i)=\textrm{min}_{k=i+1,a_k>a_i}^nk$$$. So, the sub-ranges for a query $$$[l,r]$$$ are, $$$[l,nextGreater(l)),[nextGreater(l),nextGreater(nextGreater(l))),\cdots$$$.
We can find these $$$nextGreater(i)$$$ for all $$$i$$$ using monotonic stack.
But calculating answer for each query this way is still slow, i.e. $$$O(n)$$$ per query. If we can save the starting positions of each sub-range for a query range, then we can find the starting position of the last sub-range by a binary search, and we can calculate the constributions of the sub-ranges other than the last one by suffix sum. Since, there can be different set of starting positions of the sub-ranges for different $$$l$$$, we can not pre-calculate the set of starting positions of the sub-ranges for each $$$i$$$.
Here is an important observation
There exists several (possibly zero) indices $$$j$$$ smaller than $$$i$$$ such that $$$nextGreater(j)=i$$$. If you create an edge from $$$i$$$ to $$$j$$$, this will form a single directed tree rooted at $$$n+1$$$ (assuming we append $$$\infty$$$ at the end of the array) where each node represents each index. This can be proved easily. I am leaving the proof as an exercise to the reader. Now, for each edge $$$i\rightarrow j$$$ of the tree, we can assign the contribution of the sub-range $$$[j, i)$$$ as the weight of the edge. So, now we can easily find the contribution of sub-ranges by querying the path sum on the tree. And using binary lifting, we can find out the starting index of the last sub-range for a query range.
Let's boil down the algorithm
- Without the loss of generality, let's append $$$\infty$$$ at the end of the array. Now, pre-calculate the $$$nextGreater(i)$$$ for all $$$i$$$ using monotonic stack.
- For each $$$i$$$ in range $$$[1, n]$$$, add an edge from node $$$nextGreater(i)$$$ to $$$i$$$ and assign $$$contribution([i, nextGreater(i)))=a_i\times (nextGreater(i)-i)$$$ sub-range as the weight of the edge.
- Pre-calculate the binary lifts of the formed tree.
- For each query $$$[l,r]$$$ follow:
- Get the starting position of the last sub-range using binary lifting, let's call this index $$$m$$$ and calculate the contributions of all the sub-ranges without the last one i.e. the distance from node $$$m$$$ to $$$l$$$.
- Then add the contribution of the last sub-range to the answer.
- Now, if you subtract the range sum of $$$[l, r]$$$ you will get your desired result for the query.
Let's walk through an example and understand the algorithm:
Given array $$$[4,3,2,5,1]$$$. So, the tree will look like below: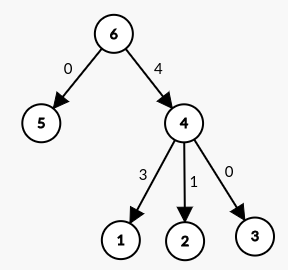
Now, let's say, we are given a query $$$(l,r)=(2,5)$$$. Using binary lifting, we find that the starting-position of the last sub-range is 4. So, our answer is $$$(\textrm{distance of 4}\rightarrow 2)+(\textrm{contribution of last range})=1+5\cdot 2-(5+1)=5$$$
Note: In general binary lifting technique $$$O(n\log n)$$$ memory is needed. That's why, here I've used a different technique mentioned in this blog which can calculate the jumps in $$$O(n)$$$ memory, and is faster than traditional LCA.
Complexity Analysis
To build the jump links, we are executing a BFS here, which is $$$O(n)$$$. And in each query, we are executing an $$$O(\log n)$$$ operation. So, the total complexity is $$$O(q\log n)$$$.
Here is my submission along with explanations, in case you need assistance.
This is my first ever solution blog. So please feel free to point out any of my mistakes.










