In this problem, it said "we partition the elements of ...". Here, the word partition should mean that we can only partition the array without shuffling the order of the elements. For example, you can partition [1,2,3,4,5] to {1,2,3} and {4,5} but not {1,3,4} and {2,5}. However, the editorial showed that you can do the latter one. To tell you i'm not misunderstanding the word "partition", here's the translation of this word with Google Translator:
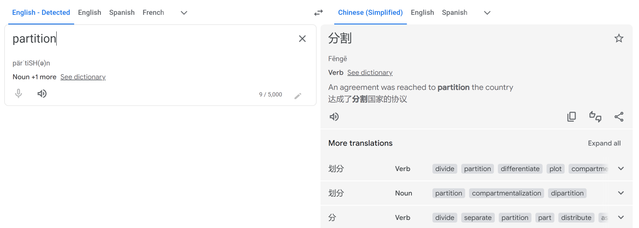
Obviously, the Chinese word "分割" shares the same meaning with what I'm talking above.
Here's the whole translation of the problem.











It said "multisets" already so I think it's fine?
I think the multiset is for this situation: there are two same elements in a block of one partition, so we can only call it "multiset" mathematically. (Same elements are illegal to be in a set due to the defintion of the set)
partition means "划分" in Chinese and the meaning of a "划分" of a set is clear
No. It is a partition of an array (not a set) in the original statement.
I'm sorry for your poor English...
I've got WA2 all the time on this problem lol
Yeah I acutally asked during the contest and they clarified it. If you reached this problem faster than me you could have asked yourself. Usually they respond within 1 minute.
I’ll claim some responsibility, but shouldn’t you get wrong answer on sample 2 if you assumed it to have to be contiguous? It’s impossible to partition 0 0 1 1 into multisets with sum of MEX 4.