| A | B | C | D | E | F1 | F2 | |
|---|---|---|---|---|---|---|---|
| nifeshe | 800 | 1200 | 1400 | 2000 | 2200 | 2700 | 2800 |
| Intellegent | 800 | 1200 | 1600 | 2000 | 2300 | ||
| mwen | 800 | 1200 | 1300 | 1800 | 2300 | ||
| Markadiusz | 800 | 1100 | 1300 | 1800 | 2300 | 2500 | 2800 |
| _istil | 800 | [1600, 2000] | 2000 | 2400 | 2700 | ||
| hazzlek | 1000 | 1200 | 1500 | 2000 | 2100 | ||
| iLoveIOI | 800 | 1100 | 1600 | 2000 | 2400 | ||
| A_G | 800 | 1100 | 1500 | 1700 | 2100 | 2600 | 2700 |
| DilshodbekX | 800 | 1200 | 1500 | 1800 | 2200 |
| A | B | C | D | E | F1 | F2 | |
|---|---|---|---|---|---|---|---|
| Average | 822 | 1163 | 1500 | 1900 | 2238 | 2550 | 2750 |
| Actual |
Look at the picture. I mean, look at the picture.
Consider coordinates $$$x$$$ and $$$y$$$ separately.
Consider coordinates $$$x$$$ and $$$y$$$ separately. Since $$$1 \le x_i, y_i \le m - 1$$$, after each step both coordinates increase and remain connected with the previous square.
From the picture we can see that each coordinate spans from the bottom-left corner of the first square to the top-right corner of the last square.
To calculate the perimeter we can add the length of that interval for both coordinates and multiply it by $$$2$$$, as it is counted in the perimeter twice, going in both directions:
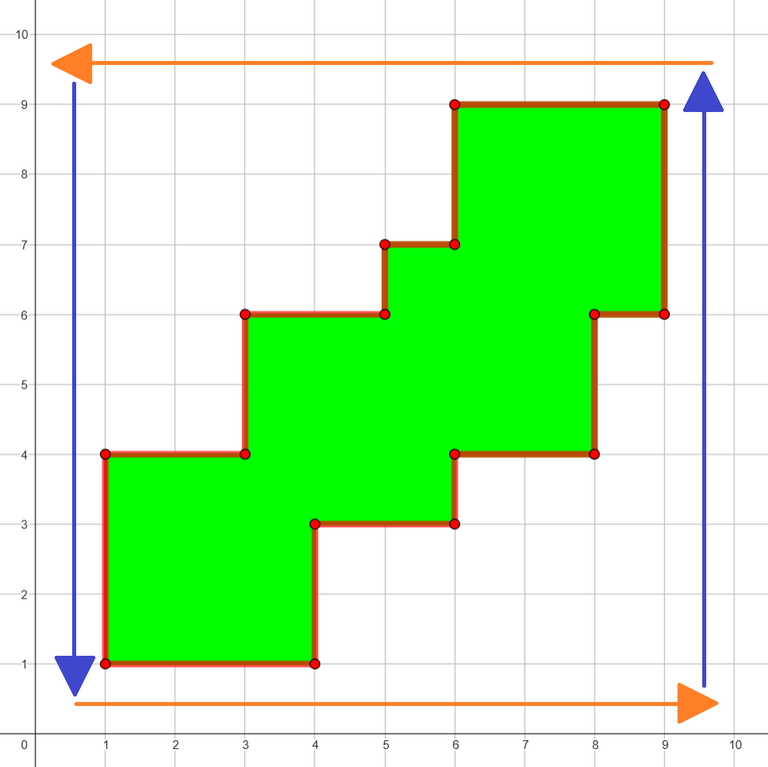
The coordinates of the bottom-left corner of the first square are $$$(x_1, y_1)$$$ and of the top-right corner of the last square are $$$(m + \sum\limits_{i = 1}^n x_i, m + \sum\limits_{i = 1}^n y_i)$$$.
The lengths of the intervals are $$$m + \sum\limits_{i = 2}^n x_i$$$ and $$$m + \sum\limits_{i = 2}^n y_i$$$.
Therefore, the answer is $$$2(2m + \sum\limits_{i = 2}^n (x_i + y_i))$$$.
#include <bits/stdc++.h>
using namespace std;
void solve() {
int n, m;
cin >> n >> m;
vector<int> x(n), y(n);
for(int i = 0; i < n; i++) {
cin >> x[i] >> y[i];
}
int ans = 2 * (accumulate(x.begin(), x.end(), 0) + m - x[0] + accumulate(y.begin(), y.end(), 0) + m - y[0]);
cout << ans << '\n';
}
signed main() {
ios_base::sync_with_stdio(0); cin.tie(0); cout.tie(0);
int ttt = 1;
cin >> ttt;
while(ttt--) {
solve();
}
}
"It can be proven that permutation $$$p$$$ can be uniquely determined"
This means that there is an order of elements. How to determine whether $$$x$$$ should be earlier in that order than $$$y$$$?
Consider two elements $$$x < y$$$. Suppose their positions in $$$p$$$ are $$$i$$$ and $$$j$$$ correspondigly.
How can we determine if $$$i < j$$$? If $$$i < j$$$ and $$$x < y$$$, we will have $$$g_{x, y} = g_{y, x} = 1$$$. Otherwise, $$$i > j$$$ and $$$x < y$$$, so $$$g_{x, y} = g_{y, x} = 0$$$.
So if $$$g_{x, y} = 1$$$, we know that $$$i < j$$$, otherwise $$$i > j$$$.
That way we can determine for each pair of elements which one of them should appear earlier in the permutation. Notice that this is just a definition of a comparator, which proves that the permutation is indeed unique. We can find it by sorting $$$p = [1, 2, \ldots, n]$$$ with that comparator.
#include <bits/stdc++.h>
using namespace std;
void solve() {
int n;
cin >> n;
vector<string> g(n);
for(auto &i : g) {
cin >> i;
}
vector<int> p(n);
iota(p.begin(), p.end(), 0);
sort(p.begin(), p.end(),
[&](int x, int y) {
if(g[x][y] == '1') return x < y;
else return x > y;
});
for(auto i : p) cout << i + 1 << " "; cout << '\n';
}
signed main() {
ios_base::sync_with_stdio(0); cin.tie(0); cout.tie(0);
int ttt = 1;
cin >> ttt;
while(ttt--) {
solve();
}
}
2056C - Palindromic Subsequences
Analyze the example with $$$n = 6$$$.
If $$$[a_1, a_2, \ldots, a_k, a_{n - k + 1}, a_{n - k + 2}, \ldots, a_n]$$$ is a palindrome, then $$$[a_1, a_2, \ldots, a_k, a_i, a_{n - k + 1}, a_{n - k + 2}, \ldots, a_n]$$$ is also a palindrome for all $$$k < i < n - k + 1$$$.
If $$$[a_1, a_2, \ldots, a_k, a_{n - k + 1}, a_{n - k + 2}, \ldots, a_n]$$$ is a palindrome, then $$$[a_1, a_2, \ldots, a_k, a_i, a_{n - k + 1}, a_{n - k + 2}, \ldots, a_n]$$$ is also a palindrome for all $$$k < i < n - k + 1$$$, because we make it's length odd and add $$$a_i$$$ to the middle.
We can use this to create a sequence with a big value of $$$g$$$. However, we shouldn't create a palindrome of a greater length than $$$2k + 1$$$ by using the fact above.
That make us try something like $$$a = [1, 2, 3, \ldots, n - 2, 1, 2]$$$. $$$f(a) = 3$$$ here, and any of $$$[a_1, a_i, a_{n - 1}]$$$ for $$$1 < i < n - 1$$$ and $$$[a_2, a_i, a_n]$$$ for $$$2 < i < n$$$ are palindromes, which means that $$$g(a) = 2(n - 3) = 2n - 6$$$.
This construction works for $$$n \ge 7$$$, so we have to handle $$$n = 6$$$ separately.
We can also use the construction from the example with $$$n = 6$$$ directly: $$$a = [1, 1, 2, 3, 4, \ldots, n - 3, 1, 2]$$$, which has $$$g(a) = 3n - 11$$$.
#include <bits/stdc++.h>
using namespace std;
void solve() {
int n;
cin >> n;
if (n == 6) {
cout << "1 1 2 3 1 2\n";
}
else if(n == 9) {
cout << "7 3 3 7 5 3 7 7 3\n";
}
else if(n == 15) {
cout << "15 8 8 8 15 5 8 1 15 5 8 15 15 15 8\n";
}
else {
for(int i = 1; i <= n - 2; i++) cout << i << " "; cout << "1 2\n";
}
}
signed main() {
ios_base::sync_with_stdio(0); cin.tie(0); cout.tie(0);
int ttt = 1;
cin >> ttt;
while(ttt--) {
solve();
}
}
Solve the problem when $$$a_i \le 2$$$.
Assign $$$b_i = 1$$$ if $$$a_i = 2$$$ and $$$b_i = -1$$$ if $$$a_i = 1$$$ and calculate the number of bad subarrays.
Extend this solution for $$$a_i \le 10$$$, however, you need to take overcounting into account.
When is a subarray $$$a[l, r]$$$ not good?
If $$$r - l + 1$$$ is odd, $$$a[l, r]$$$ can't be bad. Otherwise, suppose the median of $$$a[l, r]$$$ is $$$x$$$. Then there need to be exactly $$$\frac{r - l + 1}{2}$$$ elements in $$$a[l, r]$$$ that are $$$\le x$$$ and exactly $$$\frac{r - l + 1}{2}$$$ that are $$$> x$$$.
This gives us an idea to calculate the number of bad subarrays with a median of $$$x$$$.
Create another array $$$b$$$ of size $$$n$$$, where $$$b_i = -1$$$ if $$$a_i \le x$$$ and $$$b_i = 1$$$ otherwise.
$$$a[l, r]$$$, which has a median of $$$x$$$, is bad if and only if $$$\sum\limits_{i = l}^r b_i = 0$$$ and $$$r - l + 1$$$ is even.
Notice that the second condition is not needed, as the sum of an odd length subarray of $$$b$$$ is always odd, so it can't be zero.
Therefore, $$$a[l, r]$$$ with a median of $$$x$$$ is bad iff $$$\sum\limits_{i = l}^r b_i = 0$$$.
If there is no $$$x$$$ in $$$[l, r]$$$, then the median of $$$a[l, r]$$$ trivially can't be equal to $$$x$$$.
If there is an occurrence of $$$x$$$ in $$$a[l, r]$$$ and $$$\sum\limits_{i = l}^r b_i = 0$$$, notice that the median of $$$a[l, r]$$$ will always be exactly $$$x$$$. This is true because $$$\frac{r - l + 1}{2}$$$ smallest elements of $$$a[l, r]$$$ are all $$$\le x$$$, and there is an occurrence of $$$x$$$, so $$$\frac{r - l + 1}{2}$$$-th smallest element must be $$$x$$$.
This allows us to simply count the number of subarrays of $$$b$$$ with a sum of $$$0$$$ and with an occurrence of $$$x$$$ to count the number of bad subarrays with median $$$x$$$.
We can subtract that value from $$$\frac{n(n + 1)}{2}$$$ for all $$$x$$$ between $$$1$$$ and $$$A = 10$$$ to solve the problem in $$$O(nA)$$$.
#include <bits/stdc++.h>
using namespace std;
const int MAX = 11;
int main() {
int tests;
cin >> tests;
for(int test = 0; test < tests; test++) {
int n;
cin >> n;
vector<int> a(n);
for(auto &i : a) {
cin >> i;
}
long long ans = 0;
for(int x = 1; x < MAX; x++) {
vector<int> b(n);
for(int i = 0; i < n; i++) {
b[i] = (a[i] > x? 1 : -1);
}
int sum = n;
vector<int> pref(n);
for(int i = 0; i < n; i++) {
pref[i] = sum;
sum += b[i];
}
vector<int> cnt(2 * n + 1);
sum = n;
int j = 0;
for(int i = 0; i < n; i++) {
if(a[i] == x) {
while(j <= i) {
cnt[pref[j]]++;
j++;
}
}
sum += b[i];
ans += cnt[sum];
}
}
ans = 1ll * n * (n + 1) / 2 - ans;
cout << ans << '\n';
}
return 0;
}
Forget about counting. What is the maximum size of $$$T$$$ if $$$m = 0$$$?
It is $$$2n - 1$$$. What if $$$m$$$ isn't $$$0$$$?
It is still $$$2n - 1$$$. To prove this represent a good set as a forest.
We can always add $$$[1, n]$$$ and $$$[i, i]$$$ for all $$$1 \le i \le n$$$ to $$$S$$$. Now the tree of $$$S$$$ has exactly $$$n$$$ leaves. What if a vertex has more than $$$2$$$ children?
What is the number of solutions when $$$m = 0$$$?
It is the number of full binary trees with $$$n$$$ leaves, which is $$$C_{n - 1}$$$, where $$$C$$$ denotes the Catalan's sequence. Extend this idea to count the number of solutions for a general tree of $$$S$$$.
Any good set has a tree-like structure.
Specifically, represent $$$S$$$ as a forest the following way: segment $$$[l, r]$$$ has a parent $$$[L, R]$$$ iff $$$[l, r] \in [L, R]$$$ and $$$R - L + 1$$$ is minimized (its parent is the shortest interval in which it lies). This segment is unique (or does not exist), because there can't be two segments with minimum length that cover $$$[l, r]$$$, as they would partially intersect otherwise.
Notice that we can always add $$$[1, n]$$$ and $$$[i, i]$$$ for all $$$1 \le i \le n$$$ if they aren't in $$$S$$$ yet. Now the forest of $$$S$$$ is a tree with exactly $$$n$$$ leaves.
Suppose $$$[L, R]$$$ has $$$k$$$ children $$$[l_1, r_1], [l_2, r_2], \ldots, [l_k, r_k]$$$. If $$$k > 2$$$, we can always add $$$[l_1, r_2]$$$ to $$$S$$$, which decreases the number of children of $$$[L, R]$$$ by $$$1$$$ and increases the size of $$$S$$$ by $$$1$$$.
Therefore, in the optimal solution each segment has at most $$$2$$$ children. Having exactly one child is impossible, as we have added all $$$[i, i]$$$, so every index of $$$[L, R]$$$ is covered by its children.
This means that we have a tree where each vertex has either $$$0$$$ or $$$2$$$ children, which is a full binary tree.
We have $$$n$$$ leaves, and every full binary tree with $$$n$$$ leaves has exactly $$$2n - 1$$$ vertices, so this is always the optimal size of $$$T$$$ regardless of $$$S$$$.
To count the number of $$$T$$$, notice that when $$$m = 0$$$ the answer is the number of full binary trees with $$$n$$$ leaves, which is $$$C_{n - 1}$$$, where $$$C$$$ denotes the Catalan's sequence.
To extend this to a general tree, we can add $$$[1, n]$$$ and $$$[i, i]$$$ for all $$$1 \le i \le n$$$ to $$$S$$$.
Now suppose $$$[L, R]$$$ has $$$k \ge 2$$$ children $$$[l_1, r_1], [l_2, r_2], \ldots, [l_k, r_k]$$$. We need to merge some children. We can treat $$$[l_1, r_1]$$$ as $$$[1, 1]$$$, $$$[l_2, r_2]$$$ as $$$[2, 2]$$$, etc. This is now the same case as $$$m = 0$$$, so there are $$$C_{k - 1}$$$ ways to merge children of $$$[L, R]$$$.
Each vertex is independent of each other, so the answer is $$$\prod C_{c_v - 1}$$$ over all non-leaves $$$v$$$, where $$$c_v$$$ is the number of children of $$$v$$$.
We can construct the tree in $$$O(n \log n)$$$ by definition or in $$$O(n)$$$ using a stack.
#include <bits/stdc++.h>
using namespace std;
const int mod = 998244353;
const int MAX = 4e5 + 42;
int fact[MAX], inv[MAX], inv_fact[MAX];
int C(int n, int k) {
if(n < k || k < 0) return 0;
return (long long) fact[n] * inv_fact[k] % mod * inv_fact[n - k] % mod;
}
int Cat(int n) {
return (long long) C(2 * n, n) * inv[n + 1] % mod;
}
int binpow(int x, int n) {
int ans = 1;
while(n) {
if(n & 1) ans = (long long) ans * x % mod;
n >>= 1;
x = (long long) x * x % mod;
}
return ans;
}
void solve() {
int n, m;
cin >> n >> m;
int initial_m = m;
vector<pair<int, int>> a(m);
for(auto &[l, r] : a) {
cin >> l >> r;
}
bool was_full = 0;
vector<int> was_single(n + 1);
for(auto [l, r] : a) was_full |= (r - l + 1 == n);
for(auto [l, r] : a) {
if(l == r) was_single[l] = 1;
}
if(!was_full) {
a.push_back({1, n});
m++;
}
for(int i = 1; i <= n; i++) {
if(!was_single[i] && n != 1) {
a.push_back({i, i});
m++;
}
}
for(auto &[l, r] : a) r = -r;
sort(a.begin(), a.end());
vector<int> deg(m);
for(int i = 0; i < m; i++) {
int j = i + 1;
while(j < m) {
if(-a[i].second < a[j].first) break;
deg[i]++;
j = upper_bound(a.begin(), a.end(), make_pair(-a[j].second, 1)) - a.begin();
}
}
for(auto &[l, r] : a) r = -r;
int ans = 1;
for(int i = 0; i < m; i++) {
if(deg[i] > 0) {
assert(deg[i] >= 2);
ans = (long long) ans * Cat(deg[i] - 1) % mod;
}
}
cout << ans << '\n';
}
signed main() {
fact[0] = 1;
for(int i = 1; i < MAX; i++) fact[i] = (long long) fact[i - 1] * i % mod;
inv_fact[MAX - 1] = binpow(fact[MAX - 1], mod - 2);
for(int i = MAX - 1; i; i--) inv_fact[i - 1] = (long long) inv_fact[i] * i % mod;
assert(inv_fact[0] == 1);
for(int i = 1; i < MAX; i++) inv[i] = (long long) inv_fact[i] * fact[i - 1] % mod;
ios_base::sync_with_stdio(0); cin.tie(0); cout.tie(0);
int ttt = 1;
cin >> ttt;
while(ttt--) {
solve();
}
}
2056F1 - Xor of Median (Easy Version), 2056F2 - Xor of Median (Hard Version)
The order of the sequence doesn't matter. What if we fix the sequence $$$\text{cnt}$$$ and then calculate its contribution to the answer?
By Lucas's theorem the contribution is odd iff for each set bit in $$$n$$$ there is exactly one $$$i$$$ such that $$$\text{cnt}_i$$$ has this bit set, and $$$\sum\limits_{i = 0}^{m - 1} \text{cnt}_i = n$$$. In other words, $$$\text{cnt}$$$ has to partition all set bits in $$$n$$$. For a fixed $$$\text{cnt}$$$ with an odd contribution, what will be the median?
There is a very big element in $$$\text{cnt}$$$.
Since $$$\text{cnt}$$$ partitions the bits of $$$n$$$, there will be $$$i$$$ which has it's most significant bit. This means that $$$2\text{cnt}_i > n$$$, so $$$i$$$ will always be the median.
Suppose there are $$$p$$$ non-zero elements in $$$\text{cnt}$$$. We can partition all set bits of $$$n$$$ into $$$p$$$ non-empty subsequences and then choose which of the $$$m$$$ numbers will occur. How can we calculate the answer now?
The only time we use the value of $$$n$$$ is when we partition all of it's set bits into subsequences. That means that the answer only depends on the number of set bits in $$$n$$$, not on $$$n$$$ itself. This allows us to solve the easy version by fixing the value of $$$p$$$ and the value of the median.
To solve the hard version use Lucas's theorem again and do digit dp or SOS-dp.
The order of the sequence doesn't matter, so let's fix the sequence $$$\text{cnt}$$$ and calculate its contribution to the answer.
For a fixed $$$\text{cnt}$$$, the number of ways to order $$$a$$$ is $$$\binom{n}{\text{cnt}_0, \text{cnt}_1, \ldots, \text{cnt}_{m - 1}}$$$. By Lucas's theorem the contribution is odd iff for each set bit in $$$n$$$ there is exactly one $$$i$$$ such that $$$\text{cnt}_i$$$ has this bit set, and $$$\sum\limits_{i = 0}^{m - 1} \text{cnt}_i = n$$$. In other words, $$$\text{cnt}$$$ has to partition all set bits in $$$n$$$.
Since $$$\text{cnt}$$$ partitions the bits of $$$n$$$, there will be $$$i$$$ which has it's most significant bit. This means that $$$2\text{cnt}_i > n$$$, so $$$i$$$ will always be the median.
Suppose there are $$$p$$$ non-zero elements in $$$\text{cnt}$$$. We can partition all set bits of $$$n$$$ into $$$p$$$ non-empty subsequences and then choose which of the $$$m$$$ numbers will occur.
The only time we use the value of $$$n$$$ is when we partition all of it's set bits into subsequences. That means that the answer only depends on the number of set bits in $$$n$$$, not on $$$n$$$ itself.
So let's fix $$$p$$$ as the number of non-zero elements in $$$\text{cnt}$$$ and $$$x$$$ as the median. Denote $$$b$$$ as the number of set bits in $$$n$$$. There are $$$S(b, p)$$$ ways to partition the bits into $$$p$$$ non-empty subsequences, where $$$S$$$ denotes Stirling number of the second kind. There are $$$\binom{x}{p - 1}$$$ ways to choose which other elements will have non-zero $$$\text{cnt}$$$, because the median will always have the largest value and non-zero $$$\text{cnt}_i$$$ must be non-decreasing.
The answer is then $$$\oplus_{p = 1}^b \oplus_{x = 0}^{m - 1} \left(S(b, p) \bmod 2\right) \cdot \left(\binom{x}{p - 1} \bmod 2\right) \cdot x$$$, which we can calculate in $$$O(km)$$$, which solves the easy version.
To solve the hard version we can use Lucas's theorem again to get that the contribution of $$$x$$$ to the answer is the XOR of $$$S(b, p + 1) \bmod 2$$$ over all submasks $$$p$$$ of $$$x$$$. We can limit $$$p$$$ to be between $$$0$$$ and $$$b - 1$$$.
That means that only $$$L = \lceil \log_2 b \rceil$$$ last bits of $$$x$$$ determine whether $$$x$$$ contributes something to the answer. We can find which of $$$2^L$$$ of them will have an odd contribution by setting $$$dp_p = S(b, p + 1) \bmod 2$$$, and calculating it's SOS-dp. Then for fixed $$$L$$$ last bits it is easy to find the XOR of all $$$x < m$$$ with those bits.
Note that $$$S(n, k)$$$ is odd iff $$$(n - k) \text{&} \frac{k - 1}{2} = 0$$$, which we can derive from the recurrence, combinatorics, google or OEIS.
This solves the problem in $$$O(b \log b) = O(k \log k)$$$.
#include <bits/stdc++.h>
using namespace std;
int C(int n, int k) {
return (n & k) == k;
}
int S(int n, int k) {
return !(n - k & (k - 1 >> 1));
}
int brute_partition(int n, int m) {
vector<int> cnt;
int ans = 0;
for(int k = 1; k <= n; k++) {
if(!S(n, k)) continue;
for(int median = 1; median < m; median++) {
if(C(median, k - 1)) ans ^= median;
}
}
return ans;
}
void solve() {
int k, m;
string s;
cin >> k >> m >> s;
int n = 0;
for(auto &i : s) n += i & 1;
int ans = brute_partition(n, m);
cout << ans << '\n';
}
signed main() {
ios_base::sync_with_stdio(0); cin.tie(0); cout.tie(0);
int ttt = 1;
cin >> ttt;
while(ttt--) {
solve();
}
}
#include <bits/stdc++.h>
using namespace std;
int S(int n, int k) {
return !(n - k & (k - 1 >> 1));
}
int get(int n, int m) {
int L = __lg(n) + 1;
int up = 1 << L;
vector<int> dp(up);
for(int i = 0; i < n; i++) dp[i] = S(n, i + 1);
for(int j = 0; j < L; j++) {
for(int i = 0; i < up; i++) {
if(i >> j & 1) dp[i] ^= dp[i ^ (1 << j)];
}
}
int ans = 0;
for(int lst = 0; lst < up && lst < m; lst++) {
if(!dp[lst]) continue;
int cnt = m - 1 - lst >> L;
if(cnt & 1 ^ 1) ans ^= lst;
if(cnt % 4 == 0) ans ^= cnt << L;
else if(cnt % 4 == 1) ans ^= 1ll << L;
else if(cnt % 4 == 2) ans ^= cnt + 1 << L;
else ans ^= 0;
}
return ans;
}
void solve() {
int k, m;
string s;
cin >> k >> m >> s;
int n = 0;
for(auto &i : s) n += i & 1;
int ans = get(n, m);
cout << ans << '\n';
}
signed main() {
ios_base::sync_with_stdio(0); cin.tie(0); cout.tie(0);
int ttt = 1;
cin >> ttt;
while(ttt--) {
solve();
}
}










i feel so dumb after seeing B's solution because I used topological sort and then sorted all the elements with equal entry times in descending order
same mistake tho. In the hindsight B is actually a great problem with multiple solutions.
Here is another way to solve B -> We will construct the array by traverse each string and with each traversal we will get value at one index. permutation numbers : i = 1, 2, 3, ... Lets take i = 3. Now to find where we will place 3 in our array we simply traverse the third string and count the number of '1's before 3rd index in that string and number of '0's after third index. That gives us the index at which 3 will come. Why this works? Think Yourself gg:)
Code
or if you dont want to think you can use custom sort
did gpt tell u that
an easy solution that i came up with is start placing elements in increasing order. For each element $$$i$$$, count the number of connections $$$j$$$ such that $$$j > i$$$. for example $$$i=1$$$ , and it's connected to $$$j=3$$$ and $$$j=5$$$, so $$$count=2$$$ start from the back of the array to find the second empty position and place $$$1$$$ there. here is my submission https://codeforces.net/contest/2056/submission/301478898
Hey, i thought of an almost same solution but there is something that i am getting wrong. I implemented it by checking for each index in increasing order, the place from the back of array where it should be placed based on the count, say j. But if index j has some value already placed there, keep checking if any index k, (k=j-1;k>=0;k--) is empty and place the number there. Basically, How to process when the count that we calculate is same for 2 different numbers??
here is my submission,301471228
What ur doing there is partially correct. Here is an example where it will fail
this should output 2,3,1 but your code would yiled 3,2,1
the problem is that, for example count(2) = 1, in my code it means "I need at least 1 zero after me" , but your code says "go to second position from the back and find me the first empty slot" replace your loop with this and i think it should work
Exact same mistake, but I rewrote a recursive solution after the contest ended (something similar to Quick Sort I'd say).
submission
B killed me and C buried me :(
SpeedForces -_-
haha
Why the B looks easy here:(.I've done converting the undirected graph in directed based on pi<pj and then i had applied topological sort .Feelin dumb man
How did every single person predict that B was lower rated than C? C was much easier IMO. I think we need more lower rated testers.
Well for some people (me) B was significantly easier because the solution was pretty motivated while C was just trying random things and seeing what stuck
C was not that random if u read testcases tbh
still random for me:(
C's solution can be put fairly simple:
Answer will be of the pattern:
[1, 1, 2, 3, 4, ..... ,n-2, 1]
then the max length f(a) is 3
and the count g(a) is: (n-2) + (n-3) = 2*n-5, which is greater than n for n >= 6.
bro, you are fucking right
Yes, it was somewhat obvious like this, but why the problem C is made like this...i thought we have to maximize this f(a). And that seems to be a problem...and idk.. plz share if anyone have idea how it gonna work in that case...
if you maximize f(a) it will be equal to n like 1 1 1 1 1 1 1 1 1 you can insert 2 in between n is odd
But maximizing f(a) like this doesn't guarantee to make g(a)>n and g(a) should always get 1 like this right? I meant maximizing f(a) while meeting the same conditions, like in sample 2 f(a) could be made 5 but as of now we solved it by keeping it as 3 only..!
g(a) is no of palindromes with length==f(a) if you take f(a)=n then how will u find other palindrome of length n, g(a) will be always one and then for n>1 answer will be wrong as g(a) has to greater than n
The difficulty distribution of this match is simply a disaster.
Another solution for $$$C$$$ is for $$$n > 6$$$ construct the array $$$1,2,$$$ $$$[3...n - 2],$$$ $$$1,2$$$. Most elements will be part of two palindromes of length $$$3:$$$ $$$1,x,1$$$ and $$$2,x,2$$$. For $$$n = 6$$$ use the one in the example.
Edit: Nevermind I just realized this was mentioned in the editorial.
In C, If you realise that g(a) is 3n-11 for 6, and notice that 11 is a constant, and for each additional n, it will increase by 3, you notice that using the first construction directly solves the problem.
1,1,2...1,2 works because it follows 3n-11.
I also got idea of using 3-len palindrome just by reading this testcase
Any idea which test case is failing for my submission: 301434979 for Problem B. I used a bubble-sort-like approach.
It seems like i completely overcomplicated D, because i solved it in $$$O(nA^2 + A^4)$$$.
you reached D. haha
Can you help me improve my
Inversions()function?My Submission
For C, I just took sample solution with 15, it already gives 190 and just pushed numbers in the end like 16 17 18 ... n.
The same way, for 15 > n >= 9 I took sample solution for 9, as it gives 24.
For 6 they already gave answer.
So I only needed to solve by hand 7, 8, which I did on paper.
for 7, 8, you can also just assume adding 4 in the middle of the array for 6 will give at least 1 new palindrome, and adding a 5 after that will give at least 1 more palindrome, and you're guaranteed to not create a longer one
why lasts codeforces rounds are random ? rarely to find topics .. number Theory or graphs in first 3 problems ?!! can any one explain
What's with the constraint of n in C? Why is it so small?
Also you can just put random distinct numbers at the end of the 3rd sample answer, as g(a)=190 which is >=100
Due to the checker code? If n is larger, it is hard to check whether the output is correct or not. I guess.
Tried sort in B and failed, using another 30 min to ponder another graph solution (almost like dijkstra)... absolutely overkill for B.
Learned, though C is really too easy for some reason.
Still I conclude C << B.
yup C is easy but you can easily make wrong guesses hence increasing penalities.
A different way to approach D:(Probably easier?)
Solution :
We have to count the number of "bad" subarrays and subtract from $$$n\choose{2}$$$ + $$$n$$$.
We count the number of "bad" subarrays with a median of exactly $$$x$$$
Let for example [l,r] be a "bad" subarray, with a[ $$$\frac{l+r}{2}$$$ ] = $$$x$$$
cnt[ $$$i$$$ ] denote number of numbers in ($$$a_1,a_2 \dots a_i$$$) less than equal to $$$x$$$
Then we have that cnt[ $$$r$$$ ] — cnt[ $$$l$$$ ] = $$$\frac{r-l+1}{2} \implies $$$ 2*cnt[ $$$r$$$ ] — $$$r$$$ = 2*cnt[ $$$l$$$ -1] — ($$$l$$$ -1)
We can just store this, and check if there is an $$$x$$$ between [ $$$l$$$ , $$$r$$$ ] and increment This can be done using lower_bound.
My submission
Hope you understand the solution, if you have any queries feel free to ask, and I'll try to help if possible.
I did this approach but for "good" subarrays and ended up with the subproblem:
Given two arrays, Count all pairs i<j such that a[i] < a[j] and b[i]<b[j].
Very nice problem F!(however probably too hard for div2)
I think someone new to CP with strong math olympiad background can reasonably solve F1. And yeah, F2 is there to entertain out of contest reds even if it's not too much harder than F1 given enough CP experience
I don’t understand the editorial for D. For even length subarrays, when we are testing for x as the median, the bad scenarios seems a lot more than what the editorial depicts.
For instance, if we are testing for 9, the array 1 1 1 9 is certainly bad, but the number of numbers less than or equal to 9 is 4, not 2 as in the editorial .
However, the sum of the array [1,1,1,9] is not 0, it is -4. You only count arrays where sum is 0 and the number appears at least once.
Let's name the [(r-l+1)/2]-th element X and [(r-l+1)/2 + 1]-th element Y.
A bad array has X!=Y.
The editorial enumerate the X from 1 to 10, and count the above bad array when X is enumerated as the [(r-l+1)/2]-th element.
I have the dumbest solution using BST to solve B
301463165
Why we only update the cnt array when a[i] equal to chosen digit? I may think that when the conditieon is enough when we firstly seen the digit x? Like: n = 6, a = {1, 4, 4, 3, 1, 4} with chosen digit = 3. It only update when we at index 4 (a[4] = 3), so that we have {1, 3, 4, 4}. But there are also in the index 6, we can have an bad array {1, 1, 3, 4, 4, 4}, but in this case the author not update the cnt array.
Code:
The constraints in the question C were kind of redundant because, I solved directly from visible cases. The answer for n=15 the third case they have given is 198, so I directly gave the same array as output for n>=15 followed by 16, 17, 18... until the required length is achieved. And for n=9 => the answer was 24, so 9-15 range is also sorted. So, only ones remaining are 7,8, we can manually generate that by appending some numbers after the given array for n=6.
In the solution of D, it's a little confused by using the term "median". It took me some time to realize "median" means the (r-l+1)/2-th smallest number here.
Also, this intended solution is interesting since the observation is apparent but useful, and it seems that only few contestants came up with it.
i didnt realize that the solution for b was that simple. i have just started thats why ig. i did something like trying to find a correct candidate from indexes 1 to n in p. if the number of pairs that can be formed from this index to the last is > than the number of edges our candidate should be connected to and also the number of elements that are larger than our candidate that have not been used yet are also greater than the number of edges our candidate should be connected to then skip this candidate and move on to the next one . since that would mean we would definitely connect an edge that is not supposed to be connected. i converted the undirected to directed first for that and then did it. well the contest time was over by the time i did that lol. but it did work when i submitted it later.
I did very dumb solution for C.
For n = [6...11] find answer by hand.
For example, I realized that the prefix of "AABCABCDCDD" where different characters stands for different number gives correct answer, and I used it. As you see, we just need 4 different numbers.
Now, divide n to small parts: many 6 and one x from range [6...11]. Solve for small parts separately, with different set of numbers. Then concatenate them to one big array. It's not hard to see it will give you correct answer.
My submission.
E is solvable with xor hashing as well: 301474893
in problem C 1 1 2 3 4 5 ... 1 the maximum f(a) is 3 the first and the last one will add n-2 and the second and last one will add n-3 so 2*n -5 it worked for n>=6
yeah i did something similar just in a more convoluted way.
i did something very different for C and it took me an embarrasing amount of time, first ans = [1, 2, 3, ..., n].Then ans[n-1] = 1 and ans[(n-1)//2] = 1, essentially ans = [1, 2, 3, ... (n-1)//2 , 1, (n-1)//2 + 1 ,..., n-2, n-1, 1] and it got accepted as those 1 essentially made f(a) = 3 and g(a) = 2*(n-2).
We can even solve D by counting the good subarrays for every fixed median and sum them up.
Here is my submission.
https://codeforces.net/contest/2056/submission/301477712
5 00000 00010 00000 01000 00000 for this input jiangly's solution gives 5 3 4 2 1 while solution in editorial gives 5 4 3 2 1 and both solutions get accepted how is 'p' unique then for this case
This is an invalid input as the question mentions that there exists a valid permutation for each test case. No permutation exists for your set of input, as there is an edge between 2 and 4 but no edge between 2 and 3 or 3 and 4. (no place can be determined for 3 here, as if 3 is after 2 then there should be an edge between 2 and 3 or if 3 is before 4 then there should be an edge between 3 and 4)
Thanks for highlighting the unusual limits.
I don't seem to have received any rating yet — was this contest unrated?
same question
How to solve the C with Binary Search?
Thanks in advance!
From F:
Can someone explain this more in detail? I can't connect the dots between Lucas's theorem and this formula.
$$$\binom{n}{\text{cnt}_0, \ldots, \text{cnt}_{m - 1}} = \binom{n}{\text{cnt}_0} \cdot \binom{n - \text{cnt}_0}{\text{cnt}_1} \cdot \binom{n - \text{cnt}_0 - \text{cnt}_1}{\text{cnt}_2} \cdot \ldots$$$
So $$$\text{cnt}_0$$$ has to be a submask of $$$n$$$, $$$\text{cnt}_1$$$ has to be a submask of $$$n - \text{cnt}_0$$$, etc.
By Luca's theorem we know $$$\binom{n}{k} \equiv 1 \pmod{2} \Leftrightarrow k$$$ contains subset of bits of $$$n$$$ in binary notation.
Also we have $$$\binom{n}{cnt_0, cnt_1, \ldots, cnt_{m-1}} = \binom{cnt_0}{cnt_0} \cdot \binom{cnt_0 + cnt_1}{cnt_1} \cdot \binom{cnt_0 + cnt_1 + cnt_2}{cnt_2} \cdot \binom{cnt_0 + cnt_1 + cnt_2 + cnt_3}{cnt_3}\dots \cdot \binom{n}{cnt_{m - 1}}$$$, to make lhs an odd number, terms on rhs should all be odd numbers. Consider the last term $$$\binom{n}{cnt_{m-1}}$$$, $$$cnt_{m-1}$$$ should contains subset of bits of $$$n$$$, then consider the previous term before it $$$\binom{n-cnt_{m-1}}{cnt_{m-2}}$$$, $$$cnt_{m-2}$$$ should contains subset of bits of $$$n-cnt_{m-1}$$$ which is exactly bits in $$$n$$$ but not in $$$cnt_{m-1}$$$, then consider previous terms and so on.
This process is essentially deleting bits from $$$n$$$ and distribute them to $$$cnt$$$, then it become quite intuitive that the above claim is true.
Oh, thank you very much
you don't have to consider n = 6 / 9 /15 separately.
has f(a) = 3
and 2*(n-3) + 1 = 2n-5 palindromes! so g(a) > n for n >= 6 which fits the constraints
301414951
Solved C like nothing, bricked at B. Nice Problemset. Here's my weird solution to C. Solution
For D, I was like with a median of x: |the number of elements larger than x — the number of elements smaller x|<|the number of element of x in the sequence|. And I cannot find a good algorithm. It was too counterintutive for me to count "bad subarrays".
i think i have a better solution for c, i hope you'll like it :D it only require hardcoding for n=6 i just messed it up during the contest in second for loop where i started it from n/2 and not n/2+1
anyways good contest ~~~~~~~~~~~~ //this is code
include <bits/stdc++.h>
using namespace std;
define fio ios_base::sync_with_stdio(false), cin.tie(NULL), cout.tie(NULL)
define ll long long
void solve() { int n; cin>>n; vectortemp={1 ,1 ,2 ,3 ,1 ,2}; if(n==6){ for(auto it:temp){ cout<<it<<" "; } cout<<endl; return; } vectorarr(n); int j=1; for(int i=0;i<=n/2;i++){ arr[i]=j; j++; } j=1; for(int i=n/2+1;i<n;i++){ arr[i]=j; j++; } for(auto it:arr){ cout<<it<<" "; } cout<<endl;
}
int main() { fio; ll t; cin >> t; while (t--) { solve(); } return 0; } //this is code ~~~~~~~~~~
first time commenting don't know how it works.
I solved C differently. In sequence [1,2,3,…,n] I changed a[⌊(n+1)/2⌋]=1 and a[n]=1, so in this new sequence f(a)=3 and g(a)=n-3+n-2=2n-5 which is enough for n≥6. Here's my solution 301421526
for c just create sequence such that length of longest palindrome is 3 , putting 1 ....1 1 here all elements in between create 3 length palindrome now we have (n-2) palindromes ready now do it with 2 it will always exceed n>
I used the same idea.
~~~~~~~~ t = int(input()) for q in range(t): n=int(input()) buffer=[0]*(n+1)
adj=[buffer] for i in range(n): adj.append(list('0'+ input())) for i in range(len(adj)): for j in range(len(adj[0])): adj[i][j]=int(adj[i][j]) #print(adj) arr=[] for i in range(n,0,-1): arr.append(i) #print(arr) i=1 val=None while(i<n): j=i-1 #print(i) val=arr[i] while j>-1: if adj[val][arr[j]]==1: j-=1 if j==-1 or (j>=0 and adj[arr[i]][arr[j]]==0): #print(j+1,val) arr.insert(j+1,val) #print(arr) arr.pop(i+1) i+=1 break else: i+=1 break print(*arr)~~~~~~~~~~~~~~~~
I did B this way: first arrange in descending order 5 4 3 2 1 now 4-->5 so 4 5 3 2 1 now 3 is connected to 5 but not 4 so: 4 3 5 2 1 now 2 is to 3 and 5 4 2 3 5 1 now 1 is to 3 5 4 2 1 3 5.
managing the loop parameters was a bit confusing but it is easy to get and works all good.301490247
geeked on b
I am too dumb for Smart contests.
I did so dumb for C.I never think that f(a) can be 3 for any input,I can't solve constructive problems:(