Although two hours late,
I invite you to the Project Euler-styled mathematical contest "Gordian Knot" by IIIT-Hyderabad.
See timings here: http://bit.ly/1x9GA9P
Total duration of contest: 48hrs.
For further details, visit: http://felicity.iiit.ac.in/threads/gordian-knot/
Register yourself at: http://felicity.iiit.ac.in/register/ Prizes worth INR 12k/-
→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 158 |
| 5 | atcoder_official | 157 |
| 6 | Qingyu | 156 |
| 7 | djm03178 | 151 |
| 7 | adamant | 151 |
| 9 | luogu_official | 150 |
| 10 | awoo | 147 |
→ Find user
→ Recent actions
↑
↓
Codeforces (c) Copyright 2010-2025 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Feb/23/2025 09:00:01 (l2).
Desktop version, switch to mobile version.
Supported by
User lists


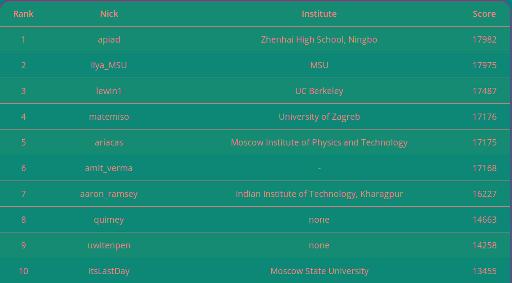
| Name |
|---|











How to solve problem about x^4 — 2*(k+2)*x^2 + (k-2)^2 polynomial?
There are two forms:
(x^3+ax^2+bx+c)(x+d) or (x^2+ax^2+bx)(x^2+cx+d)
For the first equation, you get a+d=0, b+ad=-2(k+2), c+bd=0, cd=(k-2)^2 This simplifies to (k-2)^2-2d^2(k+2)+d^4 = 0, a = -d, b = d^2-2(k+2), c = -d(d^2-2(k+2)), which are all integer if d is an integer. You can check if d has an integer solution by solving this quadratic equation.
For the second equation, you get a+c=0, b+ca+d=-2(k+2), cb+ad=0, bd = (k-2)^2
Using first/third equation, we know c=-a, so a(b-d)=0, so either a=0 or b=d If a=0, then b+d=-2(k+2) and bd = (k-2)^2, which you can check for efficiently (using binary search for instance).
Otherwise, b=d and c=-a, so we have ac=2(k+2+b) and b=(k-2) so a^2=4k. Thus, if k is a perfect square there exists a solution.
Now, it turns out you don't really need the first equation at all and can get away with just the second one, so you just need to check if k is a perfect square or there exists integers with m+n=2(k+2) and mn = (k-2)^2.
Just to clarify, the part "...or there exists integers with m+n=2(k+2) and mn = (k-2)^2" is equal to stating that equation x^2 — 2(k+2)x + (k-2)^2 has integer solutions for given k. By finding discriminant, you could see that it happens iff 8 * k is a square of integer.
So, overall, if 8 * k or 4 * k is perfect square, then this k is "good", otherwise not.
Is there any k for which the original polynomial will be a required product but won't be a product of polynomials like (x2 - A)·(x2 - B) for some A and B? I can't see any counterexample but my answer based on this idea wasn't accepted.
UPD: Nevermind, got my mistake.