Div2A: Kyoya and Photobooks
Solving this problem just requires us to simulate adding every character at every position at the string, and removing any duplicates. For instance, we can use a HashSet of Strings in Java to do this (a set in C++ or Python works as well).
Bonus: Prove that the number of ways is always (length of string + 1) * 25 + 1.
Example code: http://codeforces.net/contest/554/submission/11767578
Div2B: Ohana Cleans Up
For each row, there is only one set of columns we can sweep so it becomes completely clean. So, there are only n configurations of sweeping columns to look at. Checking a configuration takes O(n2) time to count the number of rows that are completely clean. There are n configurations in all, so this takes O(n3) time total.
Alternatively, another way of solving this problem is finding the maximum number of rows that are all the same.
Example code: http://codeforces.net/contest/554/submission/11767576
Div2C/Div1A: Kyoya and Colored Balls
Let fi be the number of ways to solve the problem using only the first i colors. We want to compute fn.
Initially, we have f1 = 1, since we only have a single color, and balls of the same color are indistinguishable. Now, to go from fi to fi + 1, we note that we need to put at a ball of color i + 1 at the very end, but the other balls of color i + 1 can go anywhere in the sequence. The number of ways to arrange the balls of color i + 1 is 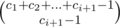 (minus one because we need to put one ball at the very end). Using this recurrence, we can solve for fn.
(minus one because we need to put one ball at the very end). Using this recurrence, we can solve for fn.
Thus, we need to precompute binomial coefficients then evaluate the product.
Example code: http://codeforces.net/contest/553/submission/11767584
Div2D/Div1B: Kyoya and Permutation
Solving this requires making the observation that only swaps between adjacent elements are allowed, and all of these swaps must be disjoint. This can be discovered by writing a brute force program, or just noticing the pattern for small n.
Here's a proof for why this is. Consider the cycle that contains n. Since n is the largest number, it must be the last cycle in the sequence, and it's the first element of the sequence. If this cycle is length 1, then we're obviously ok (we can always append (n) to the end). If the cycle is of length 2, we need n to be involved in a cycle with n - 1. Lastly, if the cycle is of length 3 or more, we will see we run into a problem. We'll only show this for a cycle of length 3 (though this argument does generalize to cycles of larger length). Let (nxy) be the cycle. So that means, n is replaced by x, x is replaced by y and y is replaced by n. So, in other words, the original permutation involving this cycle must look like
position: ... y x n
number : ... n y x
However, we need it to look like (nxy) so this case is impossible.
So, once we know that n is a in a cycle of length 1 or 2, we can ignore the last 1 or 2 elements of the permutation and repeat our reasoning. Thus, the only valid cases are when we swap adjacent elements, and all swaps are disjoint. After making this observation, we can see the number of valid permutations of length n is fib(n+1). (to see this, write try writing a recurrence).
To reconstruct the kth permutation in the list, we can do this recursively as follows: If k is less than fib(n), then 1 must be the very first element, and append the kth permutation on {1,...,n-1} with 1 added everywhere. Otherwise, add 2, 1 to the very front and append the k-fib(n)th permutation on {1,...,n-2} with 2 added everywhere.
Example code: http://codeforces.net/contest/553/submission/11767583
Div2E/Div1C: Love Triangles
Let's look at the graph of characters who love each other. Each love-connected component can be collapsed into a single node, since we know that all characters in the same connected component must love each other.
Now, we claim that the resulting collapsed graph with the hate edges has a solution if and only if the resulting graph is bipartite.
To show this, suppose the graph is not bipartite. Then, there is an odd cycle. If the cycle is of length 1, it is a self edge, which clearly isn't allowed (since a node must love itself). For any odd cycle of length more than 1, let's label the nodes in the cycle a1, a2, a3, ..., ak. Then, in general, we must have ai loves a(i + 2), since ai, a(i + 1) hate each other and a(i + 1), a(i + 2) hate each other (all indicies taken mod k). However, we can use the fact that the cycle is odd and eventually get that ai and ai + 1 love each other. However, this is a contradiction, since we said they must originally hate each other.
For the other direction, suppose the graph is bipartite. Let X, Y be an arbitrary bipartition of the graph. If we let all nodes in X love each other and all nodes in Y love each other, and every edge between X and Y hate each other, then we get a solution. (details are omitted, though I can elaborate if needed).
Thus, we can see that we have a solution if and only if the graph is bipartite. So, if the graph is not bipartite, the answer is zero. Otherwise, the second part of the proof gives us a way to count. We just need to count the number of different bipartitions of the graph. It's not too hard to see that this is just simply 2^(number of connected components — 1) (once you fix a node, you fix every node connected to it).
This entire algorithm takes O(N + M) time.
Example code: http://codeforces.net/contest/553/submission/11767582
Div1D: Nudist Beach
The algorithm idea works as follows:
Start with all allowed nodes. Remove the node with the smallest ratio. Repeat. Take the best ratio over all iterations. It's only necessary to consider these subsets. Proof for why.
We say this process finds a ratio of at least p if and only if there exists a subset with ratio at least p.
Exists a subset with ratio at least p => algorithm will find answer of at least p. First, observe that the ratio of any particular node only decreases throughout the algorithm. Thus, all nodes in this subset initally have ratio at least p. Then, the very first node that gets removed from this subset must not have ratio smaller than p, thus the above algorithm will record an answer of at least p.
Exists no subset with ratio at least p => algorithm finds answer at most p. No subset with ratio at least p implies every subset has ratio at most p. Thus, at every iteration of our algorithm, we'll get an answer of at most p, so we're done.
Thus, we can see these are necessary and sufficient conditions, so we're done.
Now for efficient implementation, we can use a variant of Dijkstra's. Recording the best subset must be done a bit more carefully as well.
Example code: http://codeforces.net/contest/553/submission/11767581
Div1E: Kyoya and Train
The Naive solution is O(MT2). Let Wj(t) be the optimal expected time given we are at node j, with t time units left. Also, let We(t) be the optimal expected time given we use edge e at time t.
Now, we have
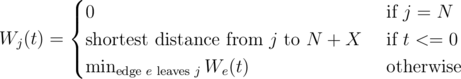
And, if e = (u->v), we have 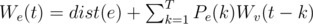
Doing all this naively takes O(MT2).
Now, we'll speed this up using FFT. We'll focus on only a single edge for now. The problem here, however, is that not all Wv values are given in advance. Namely, the Wv values require us to compute the We values for all edges at a particular time, and vice versa. So we need some sort of fast "online" version of FFT.
We do this as follows. Let's abstract away the original problem, and let's say we're given two arrays a,b, where a is only revealed one at a time to us, and b is given up front, and we need to compute c, their convolution (in the original problem b is Pe, and a is Wv, and c is We). Now, when we get the ith value of a, we need to return the ith value of the convolution of c. We can only get the ith value of a when we compute the i-1th values of c for all c.
Split up b into a block of size 1, a block of size 1, then a block of size 2, then a block of size 4, then 8, and so on.
Now, we get a0, which will allow us to compute c1, which lets us get a1, which allows us to compute c2, and so on.
So, now we have the following:
b_1 | b_2 | b_3 b_4 | b_5 b_6 b_7 b_8 | ...
We'll describe the processing of a single ai
When we get ai, we will first convolve it with the first two blocks, and add those to the appropriate entry. Now, suppose ai is multiple of a 2k for some k. Then, we will convolve ai - 2k .. ai - 1 with the block in b with the same size.
As an example.
b_1 | b_2 | b_3 b_4 | b_5 b_6 b_7 b_8 | ...
a_0 a0b1
a0b2
This gives us c0, which then allows us to get a1
b_1 | b_2 | b_3 b_4 | b_5 b_6 b_7 b_8 | ...
a_0 a0b1 a1b1
a_1 a0b2 a1b2
This gives us c1, which then allows us to get a2
a2 is now a power of 2, so this step will also additionally convolve a0, a1 with b3, b4
b_1 | b_2 | b_3 b_4 | b_5 b_6 b_7 b_8 | ...
a_0 a0b1 a1b1 a2b1
a_1 a0b2 a1b2 a2b2
a_2 a0b3 (a1b3+a0b4) a1b4
So, we can see this gives us c2, which then allowus to get a3, and so on and so forth.
Thus, this process of breaking into blocks works. As for runtime, we run FFT on a block size of B T/B times, so this term contributes (T/B) * B log B = T log B
So, we sum T log 2 + T log 4 + ... + T log 2\^(log T) <= T log\^2 T
Thus, the overall time per edge is 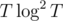 , which gives us a total runtime of
, which gives us a total runtime of 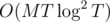 .
.
Example code: http://codeforces.net/contest/553/submission/11767579











some real quick and detailed editorials :D
Links for code are invalid :(
Oh, it seems I submitted as contest manager. Let me see if I can fix that.
I added links to code on pastebin for now.
In "Div2C/Div1A: Kyoya and Colored Balls" we can't just precompute binomial coefficients because sum(c) is 10^6
We can precompute factorials mod 10^9+7 and use them to calculate binomial in O(1).
The number of balls is at most 1000, so precomputing binomial coefficients in n^2 is enough. Though yes, you are absolutely correct for precomputing factorials instead.
Oops, I missed that line in problem text :)
In Div2-A From Which topic did the formula (l+1)*25+1 come from? I see almost everyone using the same
For a string of size n, the number of places to be filled are n+1 and it can be filled in 26 ways so (n+1)*26 but for each alphabet, say 'a', keeping the same alphabet before or after, gives the same result 'aa', so we subtract one set,i.e., one for each character in string which will be -n, so the final result is (n+1)*25+1.
for a given string "abcdef.." you can place
This will give you a formula of
26 + 25*lenCorrection: It should be
26 + 25*len11753082it is the same as
Or in problem D: we are to verify every cycle for property that number of 1's have same parity that length of cycle, which can be easily done in O(n·logn) time.
In div1 b why it should look like nxy? Question says largest element should be first not that it should be in decreasing order. So nyx seems valid. Announcement also said this. Am I wrong somewhere?
yes you are right. Problem statement is not correct. You are expected to sort each cycle in decreasing order and then compare with original cycle. so (3,1,2) should be compared to (3,2,1). However according to problem statement (3,1,2) should be compared to (3,1,2) which is what i assumed and got WA
If you take permutation 312 than cycle will be 3-2-1, and 312 isn't equal 321. If you take permutation part nxy, cycle will be nyx. More formally, if you have n{rest}x in permutation, cycle will be nx{permutation of rest}. So, if rest is not empty, permutation is invalid.
You are right. cycle for 312 would be 321 acc to defintion of cycle in problem.. In that case we don't need to sort in decreasing order. my bad!
Added lazy updates to my E and it passed =( 11751050
My initial solution did N rounds of calculating FFTs for all edges, which was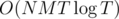 . Changing it to only update different nodes until everything stops changing allowed it to pass all tests.
. Changing it to only update different nodes until everything stops changing allowed it to pass all tests.
N rounds, not T rounds? What are you doing here :P?
I have a table of expected cost from all towns at all times (T*N), and I can update it along one road in O(T log T) using FFT. Assuming that the optimal path never visits the same town twice, we can run it for all edges N times, which will give us the answer. I submitted this 1 minute before the contest ended and it was still too slow =(
Then I changed it to a BFS-like approach, where I add the final town to the queue, then pop nodes from the queue, update all its neighbors and add those that changed into the queue again. I don't know what the complexity of this is, because it can still visit the same town multiple times, but its fast enough to pass all tests in 4 seconds.
"Assuming that the optimal path never visits the same town twice" — is it obvious? The thing is, it is not typical shortest path, maybe if it will turn out that our bus was really slow then we will want to return to the same vertex and try other edge?
Swistakk is right. Actually, the optimal path may even use the same edge twice. Here's a small example.
Here, the optimal strategy is to follow 1->2->3. If 2->3 takes 1 time unit, then take 3->4. Otherwise, take 3->1->2->4. This has expected cost 2 + (.9 * 4 + .1 * 100) = 15.6. We can see that the optimal path may use the edge 1->2 twice.
Unfortunately, I wasn't able to generalize this to larger examples in time for the contest, though I believe that I can force the optimal path to use an edge even n times in the worst case. I apologize for the weak test cases.
Interesting, I suppose the more general solution that iterates until the values stop changing would work, although it might take too long in that case. Would be interesting to see if it actually works for more difficult cases.
In problem D we can also use binary search on that ratio. Then we perform deleting bad nodes like BFS. This results in the same complexity, but I think that proof is much more intuitive.
I am struggling with getting proof for your solution. Could you kindly explain your solution to me? I mean, intuitively I understand it, but I can't come up with formal proof. :(
We need to consider a set of vertices which are bad for sure. Initially there are k bad vertices. Whenever there is a vertex which has sufficiently many bad for sure vertices he is also bad for sure. At some point of time we won't be able to add vertices to that set. If that's because we have marked all vertices as bad for sure then we are screwed. However if there are some vertices alive then they do not have sufficiently many bad for sure vertices, so they form good set for a particular ratio.
Can anyone tell my where that formula used in Div2-C comes from? I got the explanation but am unable to figure the formula part
When you add a new color, the last ball of that color will always come last, and the remaining balls are distributed among all the previous balls. If the total number of balls so far was n, and we add c balls of the new color, then we need to choose c - 1 places for balls of the new color among n + c - 1 possible places, which is possible in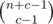 ways. Multiply that by the number of arrangements for the previous color.
ways. Multiply that by the number of arrangements for the previous color.
I am still confused..How will that cover the case when the c-1 balls are placed altogether in say the leftmost position ?
n+c-1 includes enough positions for both the old and new balls. So if you old balls are labeled as 1, and new as 2, you would have something like 22221111111.
Got it! Thanks :)
It took me also some time to understand it. We are actually using a multichoose, when counting all the possibilities to place the balls between the other balls.
Shouldn't the formula be , since we are speaking about i + 1 th color?
, since we are speaking about i + 1 th color?
Oh yes, you're right. Off by one error in editorial. Sorry about that.
can you explain why this is not working for pretest 2: we have balls 1 2 3 4.
According to formula we take 1 first.
for next color C(1 + 1, 1) = 2
for next color C(1 + 2 + 2, 2) = 20
for next color C(1 + 2 + 3 + 3, 3) = 84
1 * 2 * 20 * 84 = 3360 and not 1680 as it should be
Consider the set of balls are {1,1,2,2,3,3} So now we try to place all balls with color 1, so number of ways is 1. Extend it to color 2. Since color 2 must finish after color 1, last position will be for color 2 ie the arrangement is _ 1 _ 1 _ 2 and we can fill any number of balls of color 2 in the blank spaces. They can be filled by number of non-negative solutions to x1+x2+x3..xN. Similarly extend the code for each color.
I didn't understand the solution of div2/B... who can explain with more details? sorry for my poor english
There are two important things you should notice: 1. You can only select a column. 2. If you select a column, to 'clean' some cell in it, all the cells in that column toggle their states — '1' becomes a '0' and '0' becomes a '1'.
Now, you are required to find the maximum number of rows which can be cleaned. Pay attention to the word 'maximum' here — there is something which may not allow two rows to be clean simultaneously. Two cells in a column cannot be clean at the same time, if they begin with the opposite states. It follows from the toggling nature mentioned in [2] above.
Therefore to find the required number of rows, you need to find the maximum number of rows which are equal. (two rows are said to be equal if all their corresponding columns have the same value)
:D
For div2 C/div 1A we can also find nCr%10000009 in linear time by using inverse modulo.
where expo(x,n) is exponentiation function which returns x^n%MOD here we are using the fact that (A^-1)%m is congruent to (A^(m-2))%MOD
Thus: (nCr)%MOD=(factorial[n]*invfactorial[n-r]*invfactorial[r])%MOD; This way even of the data was given such that n was upto the range 10^7 to 10^8 you could have still most probably been able to solve the question in the given time limit.
You can see my implementation of the code on this link: http://codeforces.net/contest/554/submission/11746833
When calculating inverse modular of i!, you can calculate only
invfactorial[n]=expo(factorial[n],MOD-2). Then you can getinvfactorial[i]=(i + 1) * invfactorial[i + 1] % MOD. Because 1 / i! = (i + 1) / (i + 1)!Oh wow!! Excellent method! reduces the time complexity even further!!!
I'll remember to implement it this way next time I come across such a question. :)
There is a way to do this in O(n) without ever using exponentiation by squaring: http://codeforces.net/blog/entry/5457.
Hey Thanks For The editorials Can Any One Explain For Me Proplem Div1/A,Div2/C Im Not That Much In Math In The Code This Func Or Theses loops I Dont Know How To Trace It And Get The Idea for (int i = 1; i < MAXN; i++) { comb[i][0] = 1; for (int j = 1; j <= i; j++) { comb[i][j] = (comb[i-1][j] + comb[i-1][j-1]) % mod; } Thanks Again :D.
That code is precomputing binomial coefficients using Pascal's triangle
After the loops complete comb[i][j] will contain the value of .
.
Approach to Div 1 — Problem A using pure DP:
Let dp[i][j] denote number of ways to place first i balls such that ending position of i'th ball is j . Let total[] be prefix sum of number of balls upto ith color from color 1.
Now to find dp[i][j], consider all values from dp[i-1][j-1] to dp[i-1][total[i-1]]. Consider one such value dp[i-1][x]. Now,we can say that all balls from position x+1 to j can be filled only using ball color i (as of now). Plus we have spaces, which are not filled by balls of colors 1 to i-1 in positions 1 to x. Total number of these voids can be found easily with prefix sum.
dp[ i ][ j ] = ( Number of voids -1 ) C ( Number of balls of color i -1) We subtract 1 to indicate last ball of color i is fixed at j. We can do pascal's triangle pre computation again using simple DP
Thanks Very Much :) It Will Take From Me Some Time To UnderStand This > Thanks ManikantanV.
Here is my code,implementing the same, in case what is said is not clear http://codeforces.net/contest/553/submission/11751489
Nevermind, I got it.
An easier way to think about Div2C/Div1A is this.
Let N be the number of balls and consider the colors from the highest to the lowest. Obviously one highest color ball must be put at the very end. Decrement N and ci by one, and now you have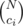 ways to place the rest of ci balls because you are free to place them anywhere. Subtract ci from N.
ways to place the rest of ci balls because you are free to place them anywhere. Subtract ci from N.
Now consider the next highest color i, the latest ball of such color must be placed at the last free position of each of the previous states, so decrement N and ci by one and compute the number of ways to place the rest of ci balls in the remaining N places. Subtract ci from N then consider the next highest color and so on ...
Hi I didn't get why we are doing combination here? I mean how is total number of ways of arranging [total_previous + C[i] -1] is total+c[i]-1 [C] c[i]-1
You do multiplication not addition
In a similar fashion (i.e. considering the colors in the decreasing order), we can go for a DP solution as well. State --> (colorToUseNext, bank).
After using the color for the first time (remember we are going backwards), we can add rest of the balls with the same color to our ball-bank (balls of which can be used anytime now).
Alternatively, we can use a ball from the ball-bank as well.
The overall idea is to construct the sequence in the reverse order, and filling the current position with either a ball from the "bank", or using a color for the first time (and adding rest of the colors to the bank, to be used later.)
I understood your logic but why are we computing ncr mod something instead of ncr.
A single integer, the number of ways that Kyoya can draw the balls from the bag as described in the statement, modulo 1 000 000 007. Because of this
In Div2/E,
What I understood is this:
According to the problem statement, if A,B-> love and B,C->love => A,C->love. Therefore in a connected component(where graph edges denote love), all nodes love each other. And if 1 node of this component hates an outside node, then all nodes will have it because if any one of it loves it => 1st 1 also loves => contracdiction. Therefore we can say that all connected components(connected by love) behave as 1 node(they love and hate the same nodes).
As for the requirement of the graph(consolidated graph by love connected components) being bipartite, it is quite clear.
Now we need to see number of such bipartite graphs we can make. If I make two partite sets, then there is no hate edge within a partite set, and no neutral state between a node is allowed => all nodes within the partite set love each other. So there will a single hate edge from partite set 1 to partite set 2.
Now we take the number of bipartite sets as 2^(no of love connected components — 1). But there is still issue I'm facing here. There are some hate relationships initally provided. When we take all cases to make a bipartite graph, wont we ignore them? What if I put two love connected component nodes in the same partite set whereas originally they hated each other? Please tell me where I'm going wrong in understanding the approach above.
Thankyou so much :D
The answer should be 2^(number of connected components including every type of edge — 1).
Please... How did you find that your D problem in div1 worths a D difficulty rating :\
I don't find anything special in it !!!!!!!!!
Scoring will be dynamic. Problems will be arranged by what I think is increasing difficulty.
you should've considered this
In Div2 B why there are only n configs of columns to watch ? I think that it should be 2^n.
Every row has only one configuration that will make it completely clean. You only need to consider those configurations (i.e. why would you consider a configuration which makes zero rows completely clean?)
There are in fact 2^n configurations, but since you only have n rows, you only need to look at the n column configurations that completely clean each of the n rows
consider a grid of nxn. We may have to clean (1)(2)(3)(4)....(n)(1,2)(1,3).....(n,n)(1,2,3)(1,2,4)... any set among 2^n to get max no. of rows cleaned. I am sorry i still didn't get it. :(
Yes, you are correct. There are 2^n ways total. However, what I'm trying to say is that you only need to look at n of them. Why is this the case? Well, why would you ever sweep a set of columns which doesn't make any row completely clean? This would lead to an answer of zero. So instead, what I'm claiming is that each row has exactly one set of columns that will make it completely clean. Since there are only n rows, there are only n interesting configurations to look at.
Got it!! Thanks . But when you say n interesting columns what do you exactly mean? Thanks for replying so fast.
Maybe it'll be clearer with an example. For the first sample `
The n interesting configurations are:
sweep the first and third column
sweep the second, third, and fourth column
sweep no columns
sweep the first and third column
There's no need to look at any other set of columns.
why my solution to problem div 2B is showing wrong answer on test 10... I used the maxm same row approach...
http://codeforces.net/contest/554/submission/11746297
Oh maybe you must write max , but you write count — that is the only mistake
to the author of "B. Ohana Cleans Up" i want to assure is test case 33 has only one zero?? then how come answer be 98. my code is giving answer 99 and i think it is correct if only one row contains 0 out of 100 rows. please answer!!
You don't see full test case. There must be one row with zeros that you cannot see
For Kyoya and colored balls, I first calculated the probability then multiplied it with all possible permutations :)
Can you please describe how you calculated the probability ?
Consider ith and (i+1)th color balls,
let total number of balls occurring before(including ith color balls) is x.
let total number of of (i+1)th balls is y.
Then the probability that i will chose the ball of (i+1)th color at end is (y)/(x+y).
I multiplied all probabilities :)
Thank you . It was helpful .
What are the prerequisites for solving problem Div 1 C.
please someone explain DIV2 D/DIV1 B in little more depth. How it reduced in Fibonacci number and how we got kth permutation using that?
let's encode our permutation like this:
b[i]=1 if a[i]<a[i+1] else 0. For example:a couple of obvious facts:
1.
001xxx<01xxxx2. no consecutive 1's allowed
These two are the rules of Fibonacci coding (check it in wikipedia), and the rest is simple.
Recent Div2D problem, very similar to this one: 551D - GukiZ and Binary Operations
ok got it. Thank you
In Div2 E , how to prove the answer is 2^(number of connected components — 1)? thanks a lot..
Number of Subsets of n objects is 2^n.
Suppose S = {1,2,3}
Number of different ways of choosing subset x numbers from S, no. of elements in x>0.
Possible subsets x = {1}, {2}, {3}, {1,2}, {1,3}, {2,3}, {1,2,3}
Left items in set S = {2,3}, {1,3}, {1,2}, {3}, {2}, {1}, {}
Now, coming to the question, we need bipartite graph. We need to find two subsets(one non-empty), that are dis-joint and complementary, we see that we can choose in 2^n/2 ways (because of repeats). And in the above example, we can do this in 4 ways(2^3/2). Give this a little thought.
Those 4 possibles are:
{1,2} and {3}
{1,3} and {2}
{2,3} and {3}
{1,2,3} and {}
thank you very much
can anybody explain Div.1B ?
Yes please some one help!
read editorial and arechitsky reply on my comment. you will get it
On div1-D(553D - Nudist Beach), the example solution 11767581 removes the node with the maximum number of non-subset neighbors, not the lowest ratio. Doesn't this variation affect the correctness of the solution? Maybe I'm too late for the question:(
I remove the nodes with the lowest ratio. Look at the compareTo method in State.
Oh I misunderstood it since I'm not java-friendly:( Thanks for the reply to this silly question!
BTW, I really like your problems! I'll study all of your problems in topcoder next week! Maybe I'll have a little confidence in Combinatorics then. :)
When you see it
Can anyone please explain how did DIV2D get fib(n) as the total number of valid permutations? If someone can provide a recursive formula , it would be great. Thanks.
If I recall correctly, this was the thought process I went through.
Let the total number of valid permutations be f(n)
f(n) = (n — 1 numbers)(1) OR (n — 2 numbers)(2 1)
= f(n — 1) + f(n — 2)
= Fibonacci numbers
Cycle with 3 or more elements can still exist, yet can't return to original sequence (see (nxy) example above)
I meant Any segments with continuous numbers. That is why I wrote it in steps :)
can anyone explain problem div2D. i get that why fib(n) permutation possible but how to find kth lexiogarphic permutation?
Suppose we want to find the k-th one.
Hope this helps.
ya i get that but i think insted of (1,2) it should (2,1)
For Div2 C, test case {1,2,3,4}. For color 1 and 2 there are only two soln 1 2 2 and 2 1 2. Now to add color 3 of three balls, we have _1_2_2_3 or _2_1_2_3. So there are four places where we can place our two 3 color balls. Can we use 4C1(i.e. 4) for putting two 3 balls together for eg 331223, 133223,123323,122333. Similarly for other case i.e. _2_1_2_3. Now we can use 4C2 (i.e. 6) to distribute two 3 color balls in _1_2_2_3 or _2_1_2_3. Eg 313223 etc. So ans till now is 20 (10 for each _1_2_2_3 and _2_1_2_3). Now to place four balls of color 4 (in those 20 combinations), ans wud be 20 * (nummber to place 4 color balls in one such way). So Now we have this kind of pattern _1_2_2_3_3_3_4, ie. total 7 places. Cant we use 7C1 (for 444), 7C2( for 44 and 4) and 7C3 (for 4 4 4), which comes out to be 7 + 21 + 35 = 63. So 63 * 20 = 1260. I am not able to get 1680 which is correct answer. What I am missing.
Anybody who can help me on this
The number of ways to put three balls of the fourth color in 122333 is equal to C(9,3) = 84. (Because the result consists of nine digits and we just need to choose which digits should be 4 and the rest of them will be filled uniquely)
But what specific case i am missing if using my way... I.e choosing 1 place for 444 (eg 4441223334) from possible 7 places, 2 places for 44 and 4 (eg 1224434334) from 7 possible places and 3 places for 4 4 4 eg (4124234334)from 7 possible places. Which permutation i am missing?
when you're choosing 2 places for 44 and 4, you do not consider that 44 can be placed before or after 4. for example both sequences 142442333 and 144242333 are valid, but you're counting only one of them.
Ohh yes! Thanks alir. It was a great help. Crystal clear now.
you're welcome :)
can anyone help me the problem of D, I use binary secrch, like this: http://codeforces.net/contest/553/submission/12397233, but if I erase the check(l) after binary search, it is wrong answer at 3, like this, http://codeforces.net/contest/553/submission/12397047, I can not understand it, can anyone help me,thank/ very much.
Beautiful Problem Div 1 B.
Sorry I am bumping this editorial. I had a doubt.
Ques C :
Why to choose two different places for each ball ? We can also place two consecutive. Can't we?
Please tell me, anyone, in kyoya and permutation where is the recurrence relation. It is simply a formulation in terms of i. It feels as if one should put n and get the answer which is absolutely wrong.
Got it.