vsanjay_nitdgp's blog

spoj make equal..
By vsanjay_nitdgp, history, 9 years ago, In English

could any one say clear logic behind this problem.

http://www.spoj.com/problems/MKEQUAL/

  • Vote: I like it
  • 0
  • Vote: I do not like it

»
9 years ago, # |
  Vote: I like it +1 Vote: I do not like it

Okay, let us first think about some way to get a lot of values to the same value.

Well couldn't we simply reduce all values to 0 and make one value as large as needed? That could always be done, just fix some value that will be huge and always increase it, decreasing others until all of them reach 0. So obviously, we could easily get an answer of N - 1. Question is — can we do better?

Obviously to do better we would need to make all N numbers equal. Let's define sum as the sum of all numbers. Clearly since after every action the sum stays constant, at the end we would want to have N numbers each with value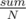 . This quickly gives us a condition — sum must be divisible by N. If that is so, we could at each iteration take the largest number and the smallest number, then increase the smallest and decrease the largest — it is easy to see that this will lead to all the numbers being equal.

So out algorithm boils down to:

1) If sum is divisible by N then print N.

2) Otherwise print N - 1

Feel free to ask any questions :)

→ Reply