TranThuyLuc's blog

Codeforces way to check precision
By TranThuyLuc, 8 years ago, In English

In many contest problems in Codeforces where the results require float point number, there is often something like this:

Namely: let's assume that your answer is a, and the answer of the jury is b. The checker program will consider your answer correct, if .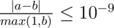

However, the normal way to check whether two float point numbers are equal is something like this:

const double EPS = 1e-9;

bool isEqual(double x, double y){
    return abs(x - y) < EPS;
}

Is the way Codeforces use more precise? Should I use this way for comparing float point numbers instead of the normal way?

  • Vote: I like it
  • +8
  • Vote: I do not like it

»
8 years ago, # |
← Rev. 2   Vote: I like it +5 Vote: I do not like it

I think they use both ways and your answer is considered correct if it's equal to the jury's answer by at least one of the two ways. More information here.

→ Reply
  • »
    »
    8 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    I think so.

    Anyway, the first way tends to work better for me, especially when I need to compare an integer with a double.

    Is there any reason to use the second way instead of the first way?

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      How do you define better in this case?

      → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        As stated in the formula, the first way also considers with the magnitude of 2 numbers.

        Therefore in case of comparing very large numbers and the precision preserved is very small, the first way will output more precise result.

        Moreover, when I extend this formula to support smaller and larger operators, the first way seem to be the only way.

        → Reply
»
8 years ago, # |
← Rev. 2   Vote: I like it +27 Vote: I do not like it

If the checker uses testlib, then the source code used is available at GitHub.

→ Reply
»
8 years ago, # |
← Rev. 2   Vote: I like it +22 Vote: I do not like it

  1. A large fraction of contest problems uses Testlib for checkers. The standard Testlib checkers include both absolute-or-relative error and absolute error checkers.

  2. Note that the absolute-or-relative check accepts strictly more answers than just the absolute check. For numbers less than one in magnitude (probabilities are an example), they are essentially the same. For large numbers, however, the absolute-or-relative check accepts more answers.
    As an example, consider EPS=1E-9 and answers of order 1E+6. If the jury answer is 1 000 000, the relative error check accepts numbers 999 999.999 through 1 000 000.001. As most solutions to contest problems use floating point for real numbers, the relative error check makes a lot of sense here.

  3. The Testlib accounts for double precision at the point of comparison as well, see what TianyiChen linked.

→ Reply