hiddentesla's blog

finding a solution for 2^x = c mod 10^9+7
By hiddentesla, history, 8 years ago, In English

problem:

given at most 400 values of C. for each C,find an integer X (X<=10^18) such that 2^x mod (10^9 + 7) = c

i know that a value x must exist (X<10^9 + 7).but finding X is a problem for me. is there an efficient way to find x?

  • Vote: I like it
  • +3
  • Vote: I do not like it

»
8 years ago, # |
  Vote: I like it +37 Vote: I do not like it

U can solve using shank baby step gaint step algorithm

→ Reply
»
8 years ago, # |
  Vote: I like it +13 Vote: I do not like it

To elaborate on teja349's answer, the idea is that there are at most m = 109 + 6 different values that 2x can take on, and if there is a solution to 2x = c, then you can writ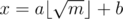e where 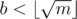and 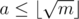(modulo off-by-one errors).

All you have to do is compute all possible 2x values where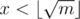 and throw them in a hashtable, and then for each value of a, check if there is some element in the hashtable having value .

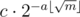→ Reply