Hello!
Some time ago I thought of the following problem:
We have a bracket sequence with length n (n ≤ 105) and we have q (q ≤ 105) queries for finding the length of the longest correct bracket substring (with consecutive elements) in a interval [l;r] (1 ≤ l ≤ r ≤ n).
Sample:
6
((()()
3
1 6 -> Answer is 4 (substring from 3rd to 6th position)
1 2 -> There is no correct bracket substring so the answer is 0
1 4 -> Answer is 2 (substring from 3rd to 4th position)
So I found a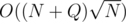 
solution with MO's algorithm but I am curious if there is an online solution. So if anyone has one, please share it. Thanks in advance.
I think this problem is the same as your question, and the editorial has the online approach explained.
I hope this will help! Happy coding!
No they aren't the same. The problem you linked is about correct bracket subsequence whereas this problem is about correct bracket substring.
It feels like the same approach should work, if you keep the best substring, the best substring from the right edge with only open left brackets and the best substring from the left edge with only open right brackets.
I don't think so. I also thought that something like that will work but couldn't find a way to merge two nodes of the segment tree.
Really? I was thinking of something like this.
Let a node know Best, BestL, BestR as before, we're merging nodes A,B. Take m to be minimum of unmatched left for A.BestR and unmatched right for B.BestL. Find the positions of the mth unmathced left for A from the right, and the mth unmatched right for B from the left. The new candidate for best is the substring between those two points.
To update BestL and BestR you also need to know whether the full substring has unmatched left of right.
Am I missing something?
Well my first idea was the same, but I couldn't find a way to find the $m$th unmached bracket in the node whose number of unmached brackets is larger. Do you have a way to do that?
Yes, use a "mergesort tree": keep an order statistics set in each node that has all the unmatched left and right brackets. Total complexity ends up being O(n log^3(n)) because of this, but it seems to work.
[Edit: Complexity corrected in light of ___'s analysis below.]
How do you make a query to such a tree? Will not be there too many merging operations?
The query is as ___ described below. You don't need to merge the sets, just ask for mth element in another mergesort tree.
It does end up being unwiededly slow, O(Q log^3 N) seems useless.
And again I thought this will work (exactly the same) but unfortunately we need to be able to merge nodes on query too.
By this I mean if we have a query interval [l;r] and the middle of the interval is mid, we cannot guarantee that the query on [l;mid] and [mid + 1;r] will cover one node (it can cover more nodes). And also we cannot just merge order statistics set for every query because it would be too slow.
Actually I just realized that in fact you would be able to do something like that because each query will cover at most
nodes. So when you do the merge for query nodes you can apply a query in another "merge sort tree" to find the mth unmatched bracket. But unfortunately it will be 
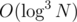this way.
PS: Just before posting this I actually realized that the merge sort tree can be replaced with a persistent segment tree and then the solution will be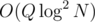
. But still if we want to be able to handle position updates the solution will be in 
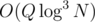. Thanks for the help. Still if you have an idea how to reduce this I would really appreciate it.
And still, how do you perform merging of nodes? Won't you be storing (in the worst case) O(length) elements within a single node corresponding to a segment of length length?
The idea is that we have two separate segment trees. Let's first talk about the first one — the one for finding the kth unmatched suffix and prefix bracket. This can be done by using divide and conquer and then in each node of the divide and conquer store the unmatched "(" suffix brackets and unmatched ")" prefix brackets (we store their indexes in sorted order). Then it's easy to get kth unmatched bracket in a range in
time by simply traveling down the tree and applying one binary search when we found the node in which the kth bracket will be. Now the second segment tree will save the following in each node: the answer, smallest position X such that all unmatched brackets in [X;r] are "(", largest position X such that all unmatched brackets in [l;X] are ")" and the count of prefix ")" and suffix "(".
When we merge we want to match the prefix ")" of [mid + 1;r] and the suffix "(" of [l;mid]. So we set m to be the lesser of the two counts and then we apply a query in the other segment tree to find the mth unmatched bracket in [mid + 1;r] if it has a prefix count bigger than m or [l;mid] otherwise.
It has O(length) merging but this is in the beginning when we build the merge sort tree.
Let me share my thoughts about this problem. It is likely that there is a bug somewhere, so please check it careful.
Firstly, we can find nextl for each l so that [l, nextl) is the shortest correct bracket substring with the left end in l. To find it, one can implement a segment tree on minimum balance values and moving left end from right to left, find this value in
for a fixed left end.
The crucial fact is that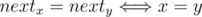
. Otherwise, [x, r) and [y, r) (r = nextx = nexty) are correct bracket substrings meaning (for x < y) that [x, y) is a correct bracket sequence too. So we can define prevr as nextprevr = r or 0 if there's no such.
That means that edges l → nextl make a graph on n + 1 vertices consisting only of chains. Our goal is to find x and y such that l ≤ x < y ≤ r + 1 and there is a chain from x to y (x → ... → y) and y - x is maximum possible.
Let's describe an offline solution firstly. One can maintain a two-dimensional segment tree, where first dimension stands for a specific chain. The second dimension stands for a vertex in that chain, so for a fixed dimension (equally chain), only values corresponding to the vertices of that chain will be meaningful, all other will be set to - INF. Thus there is exactly n + 1 non-infinity values spread among the 2D segment tree leaf elements.
For clarity, let's say chainx is the ID of the chain x belongs to (its cell in segment tree has coordinates (chainx, x)). Initially we set all (chainx, x) to - x. The meaning of this value is the maximum length of a segment starting in x.
Now let's move the right end from left to right. When its changed from r - 1 to r, some segment tree values for chainr should change, because only vertex r is added on the current step. It affects all the vertices of a chain in a simplest way — increasing their answers by r - prevr (since previously prevr was the last node in the chain). So we just need to add r - prevr to all elements with the first dimension chainr. Note that elements x > r will not count since their values will be still negative.
So for a fixed r we can answer all the queries l by making a query for a submatrix [0..num_chains)[l..n + 1) (yes, first dimension is fully occupied, so it's like the right part of the matrix). Should work in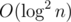
.
The online idea is just a persistency =P (consuming more memory).
I'm feeling that I'm still missing something here. But I hope that at least something is helpful here.
I didn't read your solution, but I remember this discussion (
solution) in russian.
I was trying to solve this problem (mentioned above by mr_knownothing) using segment tree but could not think of a solution. Can someone help?