Hi. I am trying to solve this problem.
For convenience, I have summarized the problem statement below.
Problem Statement
Given an array of length ≤ 2e6 containing integers in the range [0, 1e6], find the longest subarray that contains a majority element (i.e. an element that occurs > ⌊ N / 2⌋ times in a list of length N).
Time limit: 1.5s
Example
If the given array is [1, 2, 1, 2, 3, 2],
The answer is 5 because the subarray [2, 1, 2, 3, 2] from position 1 to 5 (0-indexed) has the number 2 which appears 3 > ⌊ 5 / 2⌋ times. Note that we cannot take the entire array because 3 = ⌊ 6 / 2⌋ .
My attempt
The first thing that comes to mind is an obvious brute force (but correct) solution which fixes the start and end indexes of a subarray and loop through it to check if it contains a majority element. Then we take the length of the longest subarray that contains a majority element. This works in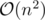 
after a small optimization. Clearly, this will not pass the time limit.
I also tried asking the same question on stack overflow, but did not receive a satisfactory answer (after several wrong suggestions and much discussion, I tried implementing the answer by Pham Trung that was given in the link, but it seems to fail on this case: [3, 3, 5, 2, 4, 1, 5]).
Could someone please advise me on a better approach to solve this problem?
I think this can be done with a range tree, assuming you also compute the answer for the left and right boundaries, since if you split up a range containing a majority element, then both halves must be one. You then only need to know if all the ranges themselves contain a majority element, which can be done in O(nlog n) by going over every depth of the segtree with a sliding window.
You can solve the problem in O(N * log(N)) by binary search + sliding window. Let 'mid' be equal to the current length which needs to be processed. Now, we need to check whether there exist any subarray having length 'mid' and containing an element with frequency = (mid / 2 + 1). This part is can be done in O(N) with the following popular approach:
1. add(i-th element)
2. remove ((i-mid)-th element).
Just keep a count and frequency array where you can track the number of occurrences of each element and frequency of each count[i] (i <= 10^6). The maximum positive value of frequency array will indicate the frequency of the current subarray.
Hi. From what I understand from your solution, I don't think it is possible to do the checking part in O(N). Because when we use a sliding window, I think we cannot update the max occurring element, for the current window, in O(1) as we move the window from left to right. I think the best we could do would be to use a range tree to perform RMQ on the array count[i] which keeps the frequency of the elements which are currently in the sliding window. Of course, this tree would also support efficient point updates so that we can update elements as we move our sliding window. An obvious candidate for this job would be segment tree.
So our complexity would be O(N*log^2N).
Please correct me if I misunderstood something.
No, you do not need segment tree. You can see that maximum of frequency array can increase by one at every iteration. The similar goes for the other operation as well.
Checking with sliding window isn't problem. Keep count in an array. This takes O(1) for moving of sliding window. You don't need to find max value in count array, it is sufficient to check if the 2 numbers that get changed are > N/2.
Binary searching doesn't seem to be applicable. In the given example there is majority element for lengths 5, 3 and 1 but not 4 and 2. It means that function isn't monotonic.
Yeah, you are right. My mistake.
First a lemma that makes the solution simpler:"There is always an optimal subarray that is a prefix or ends with a majority element. (If a non-prefix subarray doesn't end in a majority element, we can move it one step to the left without reducing the number of majority elements, so there will still be a majority.)
The prefixes can be checked in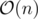
.
Process each value on its own. When processing a value x, replace each occurrence of x by 1 and each other element by - 1. A Subarray with positive sum corresponds to a subarray where x has a majority. Now build prefix sums. When looking for a longest subarray with positive sum ending in a, we can now look for the leftmost prefix sum that is smaller then the prefix sum at a. This leftmost position won't change if we do prefix-minimum after prefix sums, so let's do that. The resulting array is non-increasing, so we can binary search for the optimal position. However, the arrays we used have size n, so the total runtime is still Θ(n2) in the worst case. (One uses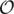
for an upper bound, Ω for a lower bound and Θ for a bound that both lower and upper.)
We can improve the above algorithm by noticing that the arrays we process are piecewise linear where the number of pieces is at most one more than twice the number of occurrences of x. (The ± 1 array is piecewise constant, so the prefix sums are piecewise linear.) We can maintain the array by maintaining it's pieces. By the lemma, we only need to check endpoints at the occurrences of x. This reduces the runtime to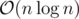
.
We can further reduce the runtime by storing a pointer to the current optimal piece in the final array. As all values in the ± 1 array are - 1 or 1, the value we query changes by at most 1, so the optimal piece changes by at most 1 (As all final pieces have slope 0 or - 1 and we can merge adjacent pieces of equal slope.) This reduces the runtime to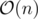
.
Hi. Thank you for your detailed explanation. I am unable to understand 2 points.
optimal subarray that is a prefix
What do you mean by prefix? Is it possible to give an example of a optimal subarray that is a prefix/not a prefix?
the number of pieces is at most one more that twice the number of occurrences of x.
What are the "pieces" that you are referring to?
Hi, thanks for asking.
(The 'that' (In your second quote) is a typo and should be a 'than'. I'll fix that.)
A prefix is a subarray that starts at the beginning of the array. (Just like a prefix sum is a sum from the beginning of the array to a position.) An example of an optimal prefix would be [1, 2, 2] in [1, 2, 2, 3, 4]. An example of an optimal non-prefix would be [1, 2, 2] in [0, 1, 2, 2, 3].
If we have a piecewise linear function, for example
on [0, 9], the number of pieces is the minimal number of line segments into which the graph of the function can be split. A piece then refers to one of those segments. (3 in the example, the 3 cases split the graph of the function into 3 segments.)
Thanks so much for clarifying! However, I still have a doubt about one detail in the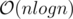
strategy.
Based on what I understand:
Let's say we use [1, 0, - 1, 0, 1, 0, - 1, - 2, - 1, 0] as the given array.
For x = 0, our prefix sum array will be:
[ - 1, 0, - 1, 0, - 1, 0, - 1, - 2, - 3, - 2]
I think there would be 7 pieces in this prefix sum array.
Now, for each prefix sum value whose corresponding value is 0 in the original array (let's call it y), we need to search for the leftmost prefix sum value that is less than y (as we want to find the longest positive sum subarray).
Naively calculating prefix sums for all distinct elements (at most ⌊ n / 2⌋ of them exist) will result in Θ(n2) complexity.
Your strategy for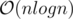
involves maintaining pieces of the prefix sum array. I am unable to visualize how these pieces would be constructed and maintained (it's my first time hearing of such a strategy). Could you please advise me?
I think he means to store all of the elements in their corresponding buckets and then the prefix sum of every element will be considered only in that bucket.
So for your array [1, 0, - 1, 0, 1, 0, - 1, - 2, - 1, 0] Bucket with id -1 will store the positions where the -1 element can be found : [2,6] This will correspond to partial sum array at the positions found in the bucket, which we can calculate easily.
Prefix sum of that bucket becomes — [-1, -5]
Might be wrong, sorry in that case
Also, dacin21 lemma seems to assume that we are looking for most occurences of majority element in subarray, though the statement seems to ask for biggest subarray, that happens to contain a majority element.
And so for array [1 5 5 5 1] lemma seems no to be applicable.
Let me know if I made a mistake, thanks :)
My algorithm looks for the longest subarray such that there is a majority in that subarray, as we internally look for the leftmost endpoint such that prefix sum is lower, which will result in the largest subarray such that the sum is positive. (Leftmost
largest, positive sum 
majority)
Your case [1, 5, 5, 5, 1] is covered by the prefix case, as the whole array is a prefix of itself.
Thanks for clarification! :)
Let's look at your case for the '-1' element. (I avoid the 0 element, as it's the most occurring and most pieces would have length 1.) The original array is (I added an imaginary '#' at the beginning to keep indices in A, B consistent with C, D. All arrays are zero-based.)
the ± 1 array is
prefix sums (Including the empty one) gives us
and prefix min gives us
Now for each occurrence of - 1 (i.e. [3, 7, 9]) we look at the value in C (for example C[9] = - 3) and search for the leftmost smaller value in D, which will be D[6] = - 4. From this we get the subarray [A[7], A[8], A[9]] = [ - 1, - 2, - 1] in which - 1 is indeed a majority.
In terms of pieces, the arrays are
and (I list the endpoints in both pieces.)
and
Instead of storing individual elements for each piece, we can simply store the index of the left endpoint, the first value and the change from one value to the next. The resulting representation is then
and (Note that there are 3 occurrences of - 1 in A, so there are at most 7 pieces in C.)
and
The computation of B follows from the array storing the occurrences of - 1. To get C from B, subtract 1 from each left endpoint, copy the value into the change and update the value by a sweep from left to right. To get D from C, sweep from left to right and whenever the value would increase, instead create a constant segment, until the current value get lower than the constant. (The number of segments doesn't increase during this step, as we remove a segment with change + 1 for every constant segment we create.)
The total number of pieces in each step is at most one more that the number of occurrences of the element, so the total number of pieces is at most 3n.