Предыстория
Жил был алгоритм Форд-Беллмана. Разные люди его по-всякому оптимизировали.
Например, популярен «Форд-Белман с очередью», также известный, как SPFA.
Здесь мы рассмотрим менее популярную версию «Форд-Белман с random shuffle».
(1) random_shuffle(edges.begin(), edges.end());
for (int run = 1; run; ) {
run = 0;
(2) random_shuffle(edges.begin(), edges.end());
for (Edge e : edges)
if (relax(e))
run = 1;
}
Фазой назовём цикл по всем рёбрам. Обычный Форд-Беллман сделает не более V фаз.
История
Оказывается, от того, где написать random_shuffle,
сделать один раз заранее, или делать в начале каждой фазы, многое зависит.
На худшем тесте матожидание числа фаз у одного из новых Форд-Беллманов равно V / 2, у другого V / 1.72.
Как думаете, у кого меньше? Скоро допишу сюда ответ и доказательства.
Если вы любите математику, но не Форд-Беллмана, вот теорвер-составляющая
int i = 0, phase = 0;
p = [0, 1, ... n-1]
(1) random_shuffle(p.begin(), p.end());
for (int i = 0; i < n; phase++) {
(2) random_shuffle(p.begin(), p.end());
for (int x : p)
if (x == i)
i++;
}
// Найти матожидание phase в зависимости от того, где random_shuffle, в (1) или (2).
UPD: правильный ответ и доказательства записал eatmore, спасибо ему.











Похоже, что тема не вызвала интереса у посетителей. ☹
Напишу-ка я свои ответы, чтобы показать, что не только Burunduk1 интересуется математикой на Codeforces. Это ответы для второй задачи, первая сводится к ней, если граф представляет собой путь из n + 1 вершин и n рёбер.
В этом случае количество фаз на единицу больше количества инверсий между соседними значениями, то есть таких пар (i, i + 1), что значение i + 1 в перестановке располагается до i. Для каждой пары вероятность того, что она будет инверсией, равна . Всего таких пар n - 1. Из линейности мат. ожидания следует, что в среднем инверсий будет
. Всего таких пар n - 1. Из линейности мат. ожидания следует, что в среднем инверсий будет 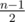 , а фаз, соответственно,
, а фаз, соответственно, 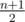 .
.
Здесь состоянием между фазами является только значение i. Пусть в начале фазы оно равно i, тогда в конце фазы оно гарантированно будет не меньше i + 1, так как число i в перестановке точно есть. Оно будет не меньше i + 2 с вероятностью , так как для этого необходимо и достаточно, чтобы значение i + 1 располагалось в перестановке после i. Оно будет не меньше i + 3 с вероятностью
, так как для этого необходимо и достаточно, чтобы значение i + 1 располагалось в перестановке после i. Оно будет не меньше i + 3 с вероятностью  , так как для этого требуется, чтобы значения i, i + 1 и i + 2 располагались по порядку. Так как все возможные относительные порядки этих значений равновероятны, каждый из них выпадает с вероятностью
, так как для этого требуется, чтобы значения i, i + 1 и i + 2 располагались по порядку. Так как все возможные относительные порядки этих значений равновероятны, каждый из них выпадает с вероятностью  . Аналогично, значение будет хотя бы i + k с вероятностью
. Аналогично, значение будет хотя бы i + k с вероятностью 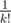 . Несложно заметить, что мат. ожидание такой величины равно
. Несложно заметить, что мат. ожидание такой величины равно  . Это всё в предположении, что процесс не упирается в конец перестановки (i = n). Но если n большое, то вероятность этого мала, и можно считать, что на каждой фазе i увеличивается в среднем на e - 1. Значит, среднее количество фаз будет примерно равно
. Это всё в предположении, что процесс не упирается в конец перестановки (i = n). Но если n большое, то вероятность этого мала, и можно считать, что на каждой фазе i увеличивается в среднем на e - 1. Значит, среднее количество фаз будет примерно равно  .
.
Почему в первом случае алгоритм более эффективный? Мне кажется, что это связано с тем, что значение i после окончания фазы находится "сразу после" инверсии, то есть до значения i - 1. Такое значение в среднем находится ближе к началу перестановки, чем равномерно распределённое значение. В первом случае алгоритм начинает каждую фазу со значения, которое в среднем ближе к началу перестановки. Во втором случае каждый раз генерируется новая перестановка, и в ней положение этого значения распределено равномерно. Если значение располагается ближе к началу, то следующее значение будет располагаться после него с большей вероятностью, чем во втором случае. Именно из-за этого в первом случае каждая фаза в среднем делает больше шагов, из-за чего в среднем требуется меньше фаз.
Ещё немного математики:
В первой фазе изменение i распределено так же, как и в случае 2. Это неудивительно, так как первые фазы в обоих случаях одинаковые. Для остальных фаз распределение другое. В частности, вероятность того, что i после фазы будет не меньше i + 2, равна . Как это доказать? Пусть очередная фаза, причём не первая, началась с некоторым значением i. Также в перестановке где-то присутствует значение i - 1 (так как фаза не первая) и i + 1 (считаем, что до n ещё далеко). Без какой-либо дополнительной информации, все шесть возможных относительных порядков этих значений равновероятны. Но мы знаем, что i ‒ начало фазы, поэтому i располагается до i - 1, и это является необходимым и достаточным условием для того, чтобы данное состояние было возможно. При этом из шести перестановок остаются только три, и в двух из них i + 1 располагается после i. Значит, новое значение i будет не меньше i + 2 с вероятностью
. Как это доказать? Пусть очередная фаза, причём не первая, началась с некоторым значением i. Также в перестановке где-то присутствует значение i - 1 (так как фаза не первая) и i + 1 (считаем, что до n ещё далеко). Без какой-либо дополнительной информации, все шесть возможных относительных порядков этих значений равновероятны. Но мы знаем, что i ‒ начало фазы, поэтому i располагается до i - 1, и это является необходимым и достаточным условием для того, чтобы данное состояние было возможно. При этом из шести перестановок остаются только три, и в двух из них i + 1 располагается после i. Значит, новое значение i будет не меньше i + 2 с вероятностью  . Рассуждая аналогично, можно придти к выводу, что значение будет не меньше i + k с вероятностью
. Рассуждая аналогично, можно придти к выводу, что значение будет не меньше i + k с вероятностью  . Мат. ожидание сдвига получается ровно 2, как и ожидалось.
. Мат. ожидание сдвига получается ровно 2, как и ожидалось.
Может показаться, что на основе этого рассуждения можно вывести точное значение мат. ожидания для количества фаз, используя динамику с i в качестве состояния. Но делать так нельзя, так как, в отличие от случая 2, перестановка также является частью состояния. Из-за неё "длины" (изменения i) разных фаз зависят друг от друга: например, фаза, следующая после более длинной фазы, скорее всего будет более короткой, чем случайно выбранная фаза. И хотя мат. ожидание количества фаз в этом случае считается очень легко (см. комментарий выше), для этого используется совершенно другой подход.
В этом случае длины разных фаз почти не зависят друг от друга: распределение длины фазы зависит только от n и i (собственно, другого состояния между фазами у алгоритма и нет). А ещё точнее, только от n - i (заметим, что нас интересует только относительный порядок значений от i до n - 1). Пользуясь этим, можно вывести рекуррентную формулу для точного мат. ожидания количества фаз:
Несколько первых значений этой функции: 1, ,
,  ,
,  ,
,  ,
,  , … Интересно, знает ли кто-нибудь нерекуррентную формулу для f?
, … Интересно, знает ли кто-нибудь нерекуррентную формулу для f?
Очень интересный пример. Конечно вариант 1 лучше, хотя некоторым может показаться, что чем случайнее, тем лучше. В первом случае события, связанные с порядком ребер в разных фазах зависимые, во втором -нет. Простой пример, почти из задачника. Пусть x,y,z — независимые равномерно распределенные непрерывные случайные величины. Тогда P(x<y)=P(x>y)=0.5 Аналогично P(y<z)=P(y>z)=0.5. Однако, P(y<z|y<x)=0.|6|