Доброго времени суток!
Недавно я решал задачи с ХХХ Всероссийской олимпиады школьников по информатике. Меня весьма поразило авторское решение задачи 6 (подобный метод я не встречал нигде).
Может ли кто-либо объяснить мне почему авторское решение на 100 баллов корректно? А именно, почему метод построения обратной перестановки и решение задачи "наоборот" работает? Связано ли это с какими-то особыми свойствами обратной перестановки? Могу ли я подобный метод использовать для любых задач на перестановки (строить обратную данной и решать задачу с конца, заменив все действия обратными им)?
Условие задачи: http://neerc.ifmo.ru/school/archive/2017-2018/ru-olymp-roi-2018-day2.pdf
Разбор: http://neerc.ifmo.ru/school/archive/2017-2018/ru-olymp-roi-2018-analysis.pdf
Я попробую объяснить. Изначально у нас есть перестановка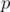
и нам нужно применять к ней перестановки 
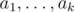, чтобы в итоге получить единичную перестановку 
:
Мы можем обратить обе стороны, учитывая, что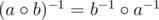
и получить:
Теперь мы можем умножить обе части на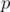
слева и на 
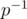справа, отчего получить форму:
То есть, в данном случае задача действительно эквивалентна тому, чтобы, применяя к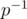
перестановки 
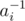, получить единичную перестановку. Заметим, что если бы мы хотели получить не единичную перестановку, а какую-то другую, скажем, 
, это, вообще говоря, корректным не было бы в том смысле, что тогда при переходе к обратным перестановкам, нам бы нужно было получить не 
, а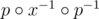 
.
Иначе говоря, утверждение верно если и только если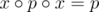
.
Спасибо большое!
Не могли бы вы мне посоветовать литературу на данную тему?
Вряд ли, я вообще литературу не очень часто штудирую, больше ориентируюсь на отдельные статьи или то, что могут написать знакомые... Можно что-нибудь по теории групп попробовать, думаю. Я в своё время знакомился с ней по "Дискретный анализ. Основы высшей алгебры" (Журавлёв Ю.И., Флёров Ю.А., Вялый М.Н.)
Там перестановки отдельно рассматриваются, насколько я помню, и несколько интересных вещей почерпнуть можно.
Еще раз спасибо