bersub's blog

Counting rectangles in a grid
By bersub, history, 7 years ago, In English

Hi!

There's a problem I'd appreciate some help with (maybe hints or a sketch of solution...)

You have an n \times n grid, with n \le 350. Every element of the grid is either '.' or '#'.

The problem asks to count the number of rectangles made of '#', where sides are bigger than or equal to 3.

So the minimal rectangle would be

###
#.#
###

IMPORTANT: There are 100 test cases, so the solution should be around O(N^2 lg N)

I tried to count the complement: As the total number of rectangles in a grid is easy to compute, I tried to focus on every dot and count the number of rectangles it interrupted, but I haven't figured out exactly how to avoid counting things multiple times...

  • Vote: I like it
  • +11
  • Vote: I do not like it

»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Auto comment: topic has been updated by bersub (previous revision, new revision, compare).

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

What about time limit, memory limit and link on original problem with tests?

→ Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

On this test:

####
####
####
####

Answer is 7?

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I see 9 rectangles in there.

    One 4x4 rectangle,

    four 3x3 rectangles.

    and four 3x4 rectangles.

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Yes, I missed two rectangles. Interesting problem! This is my solution in time O(n^2) on each query. It so happened that the idea of a solution coincides with comment: for fixed left side of rects we can sort by counting all points in left column by length of sequence of '#' from this position to right. Then we can moving right side of rectangle with increasing answer and removing sequences with length < right-left+1. But we calculate rectangles with height 2 too. After this calculations we decreasing answer on number of rectangles with height 2.

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
        ← Rev. 2   Vote: I like it 0 Vote: I do not like it

        Your solution says 16 to the following case, whereas the right answer is 5 if I'm not wrong...


        7 8
........
..#####.
.######.
.##..##.
.##..##.
.######.
........

        Your solution says the answer to this case is 16

        → Reply
        • »
          »
          »
          »
          »
          7 years ago, # ^ |
          ← Rev. 2   Vote: I like it 0 Vote: I do not like it

          Yes, I understand what's wrong. Look on this test:

          1
3 4
####
#..#
####

          My solution says that there are 3 rectangles. I will try to fix it

          And this test:

          7 4
####
#..#
####
....
####
#..#
####

          Solution says that the answer is 18, but I see 2 rectangles.

          → Reply
        • »
          »
          »
          »
          »
          6 years ago, # ^ |
          ← Rev. 3   Vote: I like it 0 Vote: I do not like it

          This solution works in O(n3) time per query, but on a worst case 100 * 355 * 355 chars '#' takes 1.72 seconds on ideone.com (without reading).

          I wrote a quick Input / Output in this solution, because the input file can have a size of 11 MB.

          Time limit less then 2 seconds?

          Solution tested on set of 1000 random tests and compared with naive solution in time O(n4)

          → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Auto comment: topic has been updated by bersub (previous revision, new revision, compare).

→ Reply
»
7 years ago, # |
  Vote: I like it +19 Vote: I do not like it

Hint: fix both left and right borders, then do something in linear time to calculate number of rectangles with such borders. That's O(n3). Optimize it by moving right border to the right instead of recalculating stuff on each step. You may need some precalculations as well. I think it should become O(n2) in the end (maybe if you move right border to the left instead and add a pinch of DSU).

→ Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it +11 Vote: I do not like it

For a certain row r we denote with Hc the amount of consecutive # symbols from cell (r, c) and above (that is, in the same column, above this cell). We'll count for each row separatedly the number of rectangles with their bottom edge at this row.

For this specific row, we look at all Hi. Given the left and right borders of the rectangle (s, e), we only need to determine the upper border of it. The count of choices for the upper border is mins ≤ i ≤ e(Hi). So given array H for this row, we want to compute the sum of minimums of all subarrays.

We can do that in , iterating from left to right while maintaining an increasing stack — a stack that contains all Hi's, such that every Hi in it is bigger than Hj, (j < i). I'd rather omit the details from here as it just becomes tedious to write down, but not hard to figure out.

This is done to each row, so .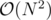

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I don't think this is exactly correct, as something like this would lead to an approach where we don't count the rectangles that have dots inside.

    I wrote this code following your idea but then I realized it fails in the cases where there are dots on the inside.

    int N, M; if(!(cin >> N >> M)) break;
        vector<string> mat(N);
        for(int i = 0; i < N; ++i){
            cin >> mat[i];
        }

        int hash_above[N][M];
        for(int i = 0; i < N; ++i){
            for(int j = 0; j < M; ++j){
                if(i == 0) hash_above[i][j] = (mat[i][j] == '#');
                else if(mat[i][j] == '.') hash_above[i][j] = 0;
                else hash_above[i][j] = 1 + hash_above[i-1][j];
            }
        }
        long long ans = 0LL;
        for(int row = 2; row < N; ++row){
            vector<int> next_right(M, -1);
            stack<int> st;
            st.push(M-1);
            next_right[M-1] = M;
            long long DP[M];
            DP[M-1] = 0LL;
            for(int i = M-2; i >= 0; --i){
                int v = hash_above[row][i];
                while(!st.empty() and hash_above[row][st.top()] >= v) st.pop();
                if(st.empty()) next_right[i] = M; else next_right[i] = st.top();
                st.push(i);
                if(v < 3) DP[i] = 0LL;
                else DP[i] = (v-2) * (next_right[i] - i >= 2 ? next_right[i] - i - 2 : 0LL) +  (next_right[i] < M ? DP[next_right[i]] : 0LL);
            }
            ans += accumulate(DP, DP + M, 0LL);
        }

        cout << ans << endl;

    Any ideas on how to fix this?

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Oh wow my bad, I (stupidly) didn't read the whole statement or even the samples :/... I thought you need to count rectangles who are full of #.

      → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Similar Question (Finding the Maximum Size Rectangle Instead)

→ Reply
»
6 years ago, # |
← Rev. 4   Vote: I like it +10 Vote: I do not like it

You can do it in O(n2log(n)), using divide & conquer.

Imagine splitting the matrix vertically at some point. We will now count the rectangles that intersect the splitting line (others will be done via recusing into the two halves).

For the rectangles that get splitted, we can observe that the left half and right half are independent if we fix the top row and bottom row. So what we will do is compute for each pair of rows, the number of half-rectangles that can be obtained with those rows as top & bottom.

Key trick: suppose the top row is the shortest (otherwise, the bottom one is the shortest, which is more or less similar).

Consider all the possible columns that are within the top row region and see how far down you can go from the top row (this can be easily precomputed). Now, each column will update a continuous prefix of bottom rows. Update all that information using some partial sums. After that, you can easily store left(i, j) and right(i, j) for i < j and row i is shorter than row j.

To count, you just add to the answer left(i, j) * right(i, j).

Total complexity is O(n2log(n)) because of master theorem

Note that to actually get the right complexity, you will have to always split the longer dimension, so you should transpose the matrix when n > m.

→ Reply