TahsinEnesKuru's blog

Upper limit for divisors divisors
By TahsinEnesKuru, history, 6 years ago, In English

What is the upper bound of total number of divisors of divisors of a number ?

  • Vote: I like it
  • +41
  • Vote: I do not like it

»
6 years ago, # |
  Vote: I like it +28 Vote: I do not like it

If a is divisor of x and y and both x and y are divisors of z, do you count a twice?

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +6 Vote: I do not like it

    yes

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
      ← Rev. 3   Vote: I like it -10 Vote: I do not like it

      then you may consider the upper bound to be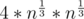 , as the upper bound on number of divisors is 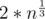(verified upto n = 1018)

      → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
          Vote: I like it +8 Vote: I do not like it

        But where does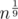 come from? Do you assume that divisors of n are of magnitude 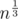? That isn't true.

        → Reply
        • »
          »
          »
          »
          »
          6 years ago, # ^ |
            Vote: I like it +37 Vote: I do not like it

          I don't know if I was high writing that... My bad :(

          → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
        ← Rev. 3   Vote: I like it +28 Vote: I do not like it

        Let f(n) be the number of divisors of divisors of n. If we are going to use a bound for d(n), we may use the identity:

        where rad(n) and ω(n) are the product and the number of distinct prime divisors of n, respectively. That formula can be obtained by noting that f is multiplicative (being the Dirichlet convolution of d and 1, or the triple Dirichlet convolution of 1), and multiplying everything after getting .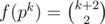

        Now, using the simple estimate

        (which comes from the fact that

        d(n) = (α1 + 1)·...·(αω(n) + 1)

        and increasing each term by 1 multiplies each bracket by at most 3/2)

        we get

        According to the last column of this table, talking only "competitive programming numbers" into account: this bound is better than the trivial

        bound by ~ an order of magnitude, but should also not be very far from the truth - the worst cases have several prime factors, with only the exponent on the prime number $2$ being significant.

        Of course, the asymptotic behaviour of d(n) has already been well-explained here, and even better on What's New. I couldn't obtain a real-world bound using this kind of approach, though.

        Also,

        Unable to parse markup [type=CF_TEX]

        is buggy here. I think there is a problem with parsing the comments.
        → Reply
»
6 years ago, # |
← Rev. 3   Vote: I like it +28 Vote: I do not like it

if your purpose is not mathematical , you can approximately find by using brute force (I mean , you don't have a time limit in your computer)

→ Reply