Siriuslight's blog

Problem BBRICKS from Codechef Long challenge
By Siriuslight, history, 6 years ago, In English

How to solve this problem using matrix exponentiation. The recurrence relation is :

f(n, k, 0) = 2 * f(n - 1, k, 1) + f(n - 1, k, 0)

f(n, k, 1) = f(n - 1, k, 1) + f(n - 1, k, 0)

1 < n < 1e9

1 < k < 1e3

  • Vote: I like it
  • 0
  • Vote: I do not like it

Comments Comments (9)
| Write comment?
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Matrix exponentiation is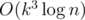 and it can be optimized to 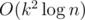, but it's too slow and may still get TLE.

I used a O(k) solution.

→ Reply
»
6 years ago, # |
← Rev. 2   Vote: I like it +1 Vote: I do not like it

I solved it by Lagrange Interpolation

Let f(n, k) denote the answer then we have the recurrence

f(n, k) - f(n - 1, k) = f(n - 1, k - 1) + f(n - 1, k - 2)

Now $f(n, 1) = 2n $ , which is linear, which implies that f(n, 2) must be quadratic, which implies that f(n, 3) must be cubic and so on..

So for fixed k, f(n, k) will be a kth degree polynomial in n, and therefore i precomputed f(n, k) for n, k upto 2000 and then I answered each test case in O(n) using Lagrange Interpolation.

So overall time complexity O(K2 + TN)

My solution for reference

→ Reply
  • »
    »
    6 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    I have heard of this term first time. Maths is really very important for progress in CP. BTW thank you for your solution.

    → Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

It can be done by combinatorics

https://www.codechef.com/viewsolution/20517309

→ Reply