2018-2019 ACM-ICPC Latin America Regional Contest

6 years ago, # ^ |

Nice observation! I coded the other one and it fit in time so I didn't think more carefully about that, maybe a little modification over limits could have done the problem more interesting :P

→ Reply

teruel

6 years ago, # ^ |

← Rev. 5 →

In fact, you only need to know the cost for a trip ending at point I, that was my AC in-contest

If you store optimal cost for trip I, then you can check 3 transitions:

1-Buy trip I and nothing after

2-Buy trip I and get next trip with a 50% discount

3-Previous transition + get any number of trips between i + 2 and i + 6 with a 75% discount

You also need to check if it's possible to buy by having sum_of_distances(i, i+k) < 120

EDIT: added solution

AC Code

#include <bits/stdc++.h>

using namespace std;

typedef long long ll;
const ll MAX = 1e6 + 5;

vector <ll> lista[MAX];

int n, d[MAX];
double dp[MAX], c[MAX];

int main() {
    ios_base::sync_with_stdio(0);
    cin.tie(0);

    cin >> n;

    for(int i = 1; i <= n; i++)
        cin >> d[i] >> c[i], dp[i] = 1e15;

    for(int i = 1; i <= n; i++) {
        dp[i] = min(dp[i], dp[i - 1] + c[i]);
        int dur = d[i];
        if(dur < 120)
            dp[i + 1] = min(dp[i + 1], dp[i - 1] + c[i] + 0.5 * c[i + 1]);
        double s = 0;
        for(int j = 1; j <= 4; j++) {
            dur += d[j + i];
            s += c[i + j + 1];
            if(dur < 120)
                dp[i + j + 1] = min(dp[i + j + 1], dp[i - 1] + c[i] + 0.5 * c[i + 1] + 0.25 * s);
        }
    }

    cout << setprecision(2) << fixed;
    cout << dp[n] << '\n';
}

→ Reply

Bashca

6 years ago, # ^ |

Problem C is possible with dijkstra too

→ Reply

SebasJM

6 years ago, # ^ |

Thanks to the peruvian team [UPC] La Señora K-ruskal for the main idea for problem B:

Two points in the circle are called opposite if are exactly separated by 180° (are at the same distance both clockwise and anti-clockwise). Having said that, if you can find at least two pairs of opposite points, you can asseverate that you can form a rectangle. See the image:

So, in order to find the pairs of opposite points you can use a set of prefix sums and find the opposite of a point doing: (x + s/2) % s, being x the current distance of the point and s the total distance sum of the circle. The s/2 means "add 180° from this position".

Code: https://ideone.com/jsIpPM

→ Reply

pipelin1010

6 years ago, # ^ |

What happens when s is not even ?

→ Reply

6 years ago, # ^ |

If s is odd, you can simply answer 'N'

→ Reply

SebasJM

6 years ago, # |

I've solved the problem L. Has been basically solved with an offline algorithm for manage the queries by your favorite update/query data structure (BIT, Segment Tree). Code: https://ideone.com/irbeZ3

→ Reply

6 years ago, # |

← Rev. 2 →

Does anyone know what is the general idea to solve problem E? Thanks

→ Reply

6 years ago, # ^ |

Fix a base. Take the edges that project on the left/right of this base. Create a tournament graph where the direction of the edges is (u, v) is directed from u to v if and only if v projects to the left of u. The task is now counting the number of 3-cycles in this graph and that's way easier. Count everything — 3-cycles that don't exist. A 3-cycle that doesn't exists will have exactly 1 vertex that has 2 out edges and exactly 1 vertex that has 2 in edges. This doesn't treat the parallel edges case (the graph isn't exactly a tournament graph) but that's easily counted apart.

→ Reply

6 years ago, # ^ |

Here's another idea, though it may be equivalent. Iterate through the sides of the polygon counter-clockwise. Suppose that we are processing some side (the green side in the picture). Consider the consecutive edges after that one, and continue until the angle with respect to the horizontal has increased by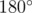 $\text{[math]}$ , the relevant portion of the polygon is cut off by the grey line in the picture. Now it's easy to see that any two edges in this section, along with the green edge, form a triple that doesn't work (the red edges in the picture for example).

With some care you can see that this process actually counts every bad triple exactly once, so just iterate over all n sides, find the number of edges in the relevant section of the polygon and find the number of pairs of these edges. Finally just subtract this from the total number of triples. We didn't solve E during the contest but this did give AC on the online judge.

→ Reply

6 years ago, # ^ |

That's equivalent, the rest of the explanation is for understanding why that counts all the bad triples once.

→ Reply

6 years ago, # ^ |

Alright, makes sense

→ Reply

JhonnyZaz

6 years ago, # ^ |

Let a[i] = Slope of ith segment, now we have to find triples of segments i < j <k such that one of the following conditions holds: a[i] > a[j] > a[k] or a[j] > a[k] > a[i] or a[k] > a[i] > a[j]. To count them easy, one can shift the array such that it only decreases once.

→ Reply

6 years ago, # |

We actually managed to solve problem L online during the contest. The idea is that we can precoumpute the answer for every value of K that is either a prime smaller than 1000 or a multiple of 1000. Then for queries with small values of K we just output the answer we calculated for the largest prime that is less than or equal to K, and for large values of K we take an m such that 1000m ≤ K < 1000m + 1000, take the answer for K = 1000m and then iterate through the primes in the interval (1000m, K]. We can see that for each one of these primes p we only need to add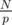 $\text{[math]}$ to the answer, because p² > 10⁵.There are not very many primes in these intervals so each query is fast enough.

→ Reply

pieromarini

6 years ago, # |

Did anyone solve problem F? Think im missing something in my implementation.

→ Reply

mrz

6 years ago, # ^ |

The max answer could be greater than 10^18, that could be your problem.

→ Reply

6 years ago, # ^ |

Didn't solve during the contest, but I got accepted on the online judge.

The idea is fairly simple, the i-th line describes a function f_i from S = [1, 2, ..., Z] to itself. It is not difficult to verify that f_i^Z(S) = f_i^Z - 1(S), so f_i restricted to S_i = f_i^Z - 1(S) is a permutation. So we can simulate the first Z steps and check whether those work manually. After that, every f_i will only move us on some cycle C_i, and we want to check whether they coincide. To do this, we try every element of C₁ as a possible common value. If this element is not in C_i for some i, then this is impossible. Otherwise the cycles give us a linear system of congruences such that each solution of it is a valid number of steps, and we can solve this using general CRT.

The implementation, at least in C++, is not easy, because even though the moduli that we build during CRT do barely fit inside a 64-bit integer, it is possible that even the sum of two numbers of that size won't fit, so you have to be extremely careful with how you do each operation in order to avoid an overflow.

→ Reply

-osdajigu-

6 years ago, # ^ |

← Rev. 3 →

How did you manage the fact that module in CRT could be 100*99*98*97*96*95*94*93*92*91 ~ 6e19, and it doesn't fit even in unsigned long long?. I solved it in Java (post-contest) but it was a pain in my neck.

→ Reply

6 years ago, # ^ |

Well, the modulo in that case is actually lcm[100, 99, ... , 91], which does fit. To be honest I don't know whether there is a case that does not fit in an unsigned long long, if there is then it wasn't included in the official test cases.

Even if it does work, I would definitely advocate for using big integers rather than trying to make it work with C++ long longs, it was extremely annoying.

→ Reply

mjhun

6 years ago, # ^ |

+31

The largest modulo I could come up with is with [99, 97, 95, 94, 91, 89, 83, 79, 73, 71] which exceeds 2⁶⁴.

I don't get the decision of the problem-setter regarding the constraints. Having for example B ≤ 5 would be exactly the same problem, but without that unnecessary annoyance with the overflows...

→ Reply

6 years ago, # ^ |

During the contest, you could use 128 bit integers.

→ Reply

ArepitaDePernil

6 years ago, # |

What is the expected solution for problem C? using C++ and a DP[time][pos] gives me a 0.850 AC with a 1 second time limit I believe it should be optimized further?

→ Reply

teruel

6 years ago, # ^ |

please read my previous comment

→ Reply

-osdajigu-

6 years ago, # |

How to solve K?

→ Reply

naumazeredo

6 years ago, # ^ |

The greatest positive sum is the sum of all positive numbers. The second greatest positive sum must be the greatest positive sum removing the smallest positive number or adding the smallest (in absolute value) negative number. This can be proven mathematically, but I won't do this right now.

So, the basic idea is to test both alternatives: removing the smallest positive number or adding the smallest negative number. To test if this candidate number is an option, half the sums must contain this number while the other half must not contain it, so you just need to check if this holds. The easiest way is taking the greatest remaining sum and checking if exists the this sum minus your candidate (if the candidate is positive. If it's negative you must check if exists this sum plus your candidate).

The sums must reduce by half every step, so you have a binary tree with height N. The complexity to do this is 2^N on every level of the tree, so N*2^N in total.

I don't think there are multiple solutions to this problem, but if there are you must be able to just store the answers on a set of sets and print them in order, but talking to contestants after the contest they didn't do this and got accepted (I just assumed the answer was unique)

→ Reply

VLamarca

6 years ago, # ^ |

← Rev. 2 →

+11

The answer is not unique. See this case for example: -3 -2 -1 0 0 1 2 3

Here are two possible answers: -3 1 2 and -2 -1 3

→ Reply

naumazeredo

6 years ago, # ^ |

Okay, so you must calculate every one of them and print in lexicografical order. I don't think there's a smart way to do this. Using set of sets you end up with O(N^2*2^N) or O(N^3*2^N). Is there any better way?

→ Reply

6 years ago, # ^ |

That's enough. Not every mask will be an answer too so it has good constant. There are at most 2^N answers and inserting one has cost N^2 at most. To make it even faster, you could push them into a vector and sort later, that has way better constant than using a set.

→ Reply

naumazeredo

3 years ago, # ^ |

Coming back after some years (someone just asked me about this problem and I decided to implement the solution, so seems okay to add more information here):

The solution is exactly what was described above. Checking for both minimum positive and maximum negative is required. You can do a divide and conquer to find the solutions.

The tricky part is avoiding O(N^2) complexity on the divide part of the D&C, that brings the complexity to O(N^3*2^N) (at least on URI OJ I got TLE with multiset or vector+binary search. Maybe in the actual contest the machines were better and the time limit was more forgiving).

The good part is that it's not hard to bring this down to O(N). You want to find a matching pair of values: x and y, so that abs(x — y) = abs(element being removed), and since this difference is constant using two pointers (or storing the elements that you want to ignore and checking when against them while advancing) allows this part to become linear.

→ Reply

pabloskimg

6 years ago, # |

← Rev. 2 →

How to solve problems G, I and J?

→ Reply

6 years ago, # ^ |

← Rev. 4 →

For problem I, first we divide a stick man by levels as follows:

Now, we can use dynamic programming to solve the problem, f(node, level) = maximum number of stick men that we can make if we are in node node and our current stick man is at level level.

→ Reply

notking

6 years ago, # ^ |

Can you share the code for this problem?

→ Reply