I'm trying to understand David Pisinger's balanced algorithm for the subset-sum problem with bounded weights, which can be found on page 5 of his paper Linear Time Algorithms for Knapsack Problems with Bounded Weights (link). Before asking this question I have read the following sources:
- https://codeforces.net/blog/entry/98663 (skip to Subset Sum Speedup 2)
- https://atcoder.jp/contests/abc221/editorial/2743
- https://stackoverflow.com/questions/18821453/bounded-knapsack-special-case-small-individual-item-weight-is-small-compared-t
I even found this code that implements it for a specific problem: https://atcoder.jp/contests/abc221/submissions/26323758
However, I wasn't able to fully understand the algorithm and its correctness based on those links, so I decided to read the paper itself. Yet, I'm not fully understanding the paper's explanation either. I will paste a screenshot of the algorithm's pseudo-code in the paper and ask specific questions about some sections:
Line 3 doesn't make sense to me. A priori we do not know if there exists a subset of items from 1 to b-1 that can exactly add up to the weight μ, for μ in [C+1, C+W]. I understand that assigning 1 means that we are hoping that there must be at least 1 possible assignment without fixing any prefix (1 means no restrictions on the weights), but, as I said, it could be the case that for some μ this is not possible, then Sb-1(μ) should be 0 instead of 1 (just like in line 2). So why is this line okay?
Line 7 doesn't seem correct. If we do a balanced insertion of wt, one possible case that could happen is that st-1(μ) == t, that is, all weights from 1 to t-1 are in the subset, and therefore by inserting wt we are extending this to t+1. In other words, the update in line 7 should be something like:
st(μ') = max{ st(μ'), st-1(μ) == t ? t + 1 : st-1(μ) }
Am I missing or misunderstanding something? Why not doing this is okay?
- I would appreciate further explanations of lines 8 and 9. I'm not clearly seeing why this successfully covers all cases of balanced deletions. How can we know that this amortization optimization is not missing any cases? Can this be proven with induction or some other technique?
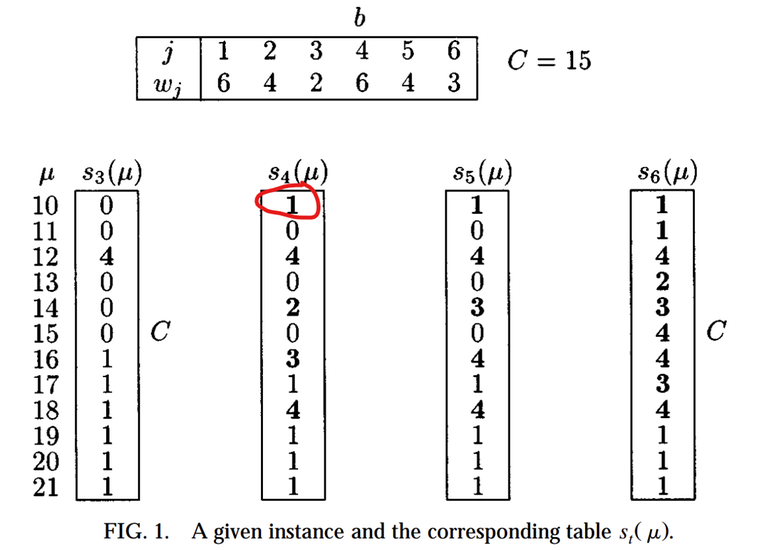
Lastly, I have a question about figure 1 on page 6 of the paper:
I highlighted s4(10). According to me, s4(10) should be 3, not 1, because we can achieve a weight of μ = 10 by adding w1 = 6 and w2 = 4 (with total weight of 10), and then we remove weights w3 and w4. Hence the rightmost index <= 4 such that we fix everything before that index and make binary choices from that index onwards would be 3, not 1. Or am I missing or misunderstanding something?



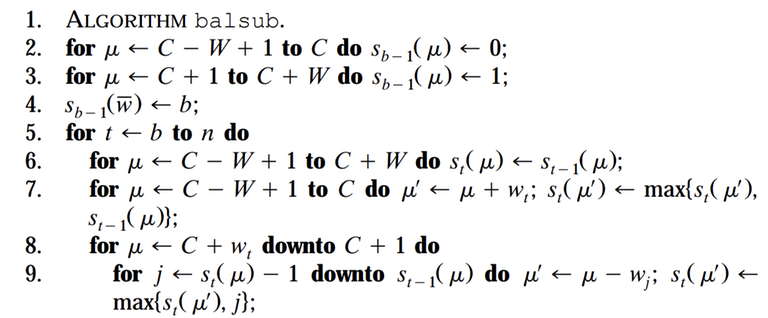






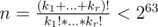 and
and 

