usernameson's blog

Does the convex hull trick work in 3 or more dimensions?
By usernameson, history, 6 years ago, In English

Let's say we have a set of planes of the form zi = aix + biy + c. Each plane will have a (possibly empty) region of 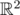where it has the maximum z value over all the planes in the set. I am wondering if these regions have sufficiently nice properties that they can be maintained, updated and queried efficiently.

  • Vote: I like it
  • +35
  • Vote: I do not like it

»
6 years ago, # |
  Vote: I like it -10 Vote: I do not like it

Yeah I guess so. The only property that is important is monotonicity. One important point to note here is that unlike the 2d version of the trick where only a single point is involved, a line should be the criterion for querying.

→ Reply
»
6 years ago, # |
  Vote: I like it +51 Vote: I do not like it

In 3 dimensions, it is possible, but a bit tricky to implement and was discussed here. Queries and insertions run in . The basic idea in 3D is that you do scanline over one dimension and maintain a changing 2D-convex hull data structure. The scanline is computed by divide-and-conquer.

In d dimensions, the convex hull can have faces, so I wouldn't expect an efficient solution for d ≥ 4.

→ Reply
»
6 years ago, # |
  Vote: I like it +26 Vote: I do not like it

i don't even know how it works in 2dimensions

→ Reply