Tutorial is loading...
Code
#include <bits/stdc++.h>
#define N 510
using namespace std;
char a[N][N];
int n;
int main(){
scanf("%d", &n);
for (int i = 1; i <= n; i++){
scanf("%s", a[i] + 1);
}
int ans = 0;
for (int i = 2; i < n; i++){
for (int j = 2; j < n; j++){
if (a[i][j] == 'X' && a[i - 1][j - 1] == 'X' && a[i - 1][j + 1] == 'X'
&& a[i + 1][j - 1] == 'X' && a[i + 1][j + 1] == 'X'){
ans ++;
}
}
}
printf("%d\n", ans);
return 0;
}
Tutorial is loading...
Code
#include <bits/stdc++.h>
#define N 300010
#define PII pair<int, int>
using namespace std;
typedef long long LL;
int n, m, a[N], c[N], t, d;
LL ans = 0;
priority_queue<PII, vector<PII>, greater<PII> > Q;
int main(){
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++){
scanf("%d", &a[i]);
}
for (int i = 1; i <= n; i++){
scanf("%d", &c[i]);
Q.push(make_pair(c[i], i));
}
for (int i = 1; i <= m; i++){
scanf("%d%d", &t, &d);
if (d <= a[t]){
a[t] -= d;
printf("%lld\n", 1LL * d * c[t]);
} else {
bool flag = false;
LL ans = 1LL * a[t] * c[t];
d -= a[t];
a[t] = 0;
while (!Q.empty()){
while (!Q.empty() && a[Q.top().second] == 0) Q.pop();
if (Q.empty()) break;
PII now = Q.top();
if (d <= a[now.second]){
a[now.second] -= d;
ans += 1LL * d * now.first;
flag = true;
printf("%lld\n", ans);
break;
} else {
ans += 1LL * a[now.second] * now.first;
d -= a[now.second];
a[now.second] = 0;
Q.pop();
}
}
if (!flag){
puts("0");
}
}
}
}
Tutorial is loading...
Code
#include <bits/stdc++.h>
#define N 300010
using namespace std;
typedef long long LL;
int n, a[N];
LL ans = 0;
int main(){
scanf("%d", &n);
for (int i = 1; i <= n; i++){
scanf("%d", &a[i]);
}
sort(a + 1, a + n + 1);
for (int i = 1; i <= n / 2; i++){
ans += 1LL * (a[i] + a[n - i + 1]) * (a[i] + a[n - i + 1]);
}
printf("%lld\n", ans);
return 0;
}
Tutorial is loading...
Code
#include <bits/stdc++.h>
#define N 300010
using namespace std;
typedef long long LL;
priority_queue<int, vector<int>, greater<int> > Q;
vector<int> e[N];
vector<int> seq;
bool vis[N];
int n, m;
int main(){
scanf("%d%d", &n, &m);
for (int i = 1; i <= m; i++){
int u, v;
scanf("%d%d", &u, &v);
e[u].push_back(v);
e[v].push_back(u);
}
vis[1] = true;
Q.push(1);
while (!Q.empty()){
int now = Q.top();
Q.pop();
seq.push_back(now);
for (auto p : e[now]){
if (!vis[p]){
Q.push(p);
vis[p] = true;
}
}
}
for (auto p : seq){
printf("%d ", p);
}
puts("");
return 0;
}
Tutorial is loading...
Code
#include <bits/stdc++.h>
#define N 100010
using namespace std;
typedef long long LL;
struct Event{
int d, w, t;
bool operator < (const Event &e) const {
return w > e.w || (w == e.w && d > e.d);
}
};
vector<Event> e[N];
Event a[N];
map<Event, int> cur;
int n, m, k;
LL f[2][N], ans = 0x3f3f3f3f3f3f3f3fLL;
void insert(Event x){
if (cur.count(x)){
cur[x] ++;
} else {
cur[x] = 1;
}
}
void erase(Event x){
cur[x] --;
if (cur[x] == 0){
cur.erase(x);
}
}
int main(){
scanf("%d%d%d", &n, &m, &k);
for (int i = 1; i <= k; i++){
int s, t, d, w;
scanf("%d%d%d%d", &s, &t, &d, &w);
e[s].push_back((Event){d, w, 1});
e[t + 1].push_back((Event){d, w, -1});
}
for (int i = 1; i <= n; i++){
for (auto p : e[i]){
if (p.t == 1){
insert(p);
} else {
erase(p);
}
}
if (cur.size()){
a[i] = (*cur.begin()).first;
} else {
a[i] = (Event){i, 0, 0};
}
}
memset(f, 0x3f, sizeof(f));
f[0][1] = 0;
for (int j = 0; j <= m; j++){
memset(f[(j ^ 1) & 1], 0x3f, sizeof(f[(j ^ 1) & 1]));
for (int i = 1; i <= n; i++){
f[(j ^ 1) & 1][i + 1] = min(f[(j ^ 1) & 1][i + 1], f[j & 1][i]);
f[j & 1][a[i].d + 1] = min(f[j & 1][a[i].d + 1], f[j & 1][i] + a[i].w);
}
ans = min(ans, f[j & 1][n + 1]);
}
printf("%lld\n", ans);
return 0;
}
Tutorial is loading...
Code
#include <bits/stdc++.h>
#define N 210
using namespace std;
typedef long long LL;
const LL p = 998244353;
const LL g = 3;
int k;
LL n, m, b[N];
struct Matrix{
int n;
LL mat[N][N];
Matrix(){
n = 0;
memset(mat, 0, sizeof(mat));
}
Matrix(int _n, LL diag){
n = _n;
memset(mat, 0, sizeof(mat));
for (int i = 1; i <= n; i++){
mat[i][i] = diag;
}
}
Matrix(const Matrix &c){
n = c.n;
for (int i = 1; i <= n; i++){
for (int j = 1; j <= n; j++){
mat[i][j] = c.mat[i][j];
}
}
}
Matrix operator * (const Matrix &a) const {
Matrix ans = Matrix(n, 0);
for (int k = 1; k <= n; k++){
for (int i = 1; i <= n; i++){
for (int j = 1; j <= n; j++){
ans.mat[i][j] += mat[i][k] * a.mat[k][j];
ans.mat[i][j] %= (p - 1);
}
}
}
return ans;
}
Matrix mat_pow(LL t){
Matrix base = Matrix(*this), ans = Matrix(n, 1);
while (t){
if (t & 1){
ans = ans * base;
}
base = base * base;
t >>= 1;
}
return ans;
}
};
namespace GCD{
LL gcd(LL a, LL b){
if (!b) return a;
return gcd(b, a % b);
}
LL ex_gcd(LL a, LL b, LL &x, LL &y){
if (!b){
x = 1; y = 0;
return a;
}
LL q = ex_gcd(b, a % b, y, x);
y -= a / b * x;
return q;
}
}
namespace BSGS{
LL qpow(LL a, LL b, LL p){
LL ans = 1, base = a;
while (b){
if (b & 1){
(ans *= base) %= p;
}
(base *= base) %= p;
b >>= 1;
}
return ans;
}
LL inv(LL x, LL p){
return qpow(x, p - 2, p);
}
map<LL, LL> tab;
LL bsgs(LL a, LL b, LL p){
LL u = (LL) sqrt(p) + 1;
LL now = 1, step;
for (LL i = 0; i < u; i++){
LL tmp = b * inv(now, p) % p;
if (!tab.count(tmp)){
tab[tmp] = i;
}
(now *= a) %= p;
}
step = now;
now = 1;
for (LL i = 0; i < p; i += u){
if (tab.count(now)){
return i + tab[now];
}
(now *= step) %= p;
}
throw;
return -1;
}
}
namespace SOL{
LL solve(LL a, LL b, LL c){
if (c == 0) return 0;
LL q = GCD::gcd(a, b);
if (c % q){
return -1;
}
a /= q, b /= q, c /= q;
LL ans, _;
GCD::ex_gcd(a, b, ans, _);
(ans *= c) %= b;
while (ans < 0) ans += b;
return ans;
}
}
int main(){
scanf("%d", &k);
for (int i = 1; i <= k; i++){
scanf("%d", &b[i]);
b[i] %= (p - 1);
}
scanf("%lld%lld", &n, &m);
Matrix A = Matrix(k, 0);
for (int i = 1; i <= k; i++){
A.mat[1][i] = b[i];
}
for (int i = 2; i <= k; i++){
A.mat[i][i - 1] = 1;
}
A = A.mat_pow(n - k);
LL ans = SOL::solve(A.mat[1][1], p - 1, BSGS::bsgs(g, m, p));
if (ans >= 0){
printf("%lld\n", BSGS::qpow(g, ans, p));
} else {
puts("-1");
}
return 0;
}











Problem E should have 512MB(or 1GB) of Memory limit :(
My code Improved version
In the author's solution, DP state reduction is used.
Yeah, state reduction.
But in polygon, the system warns if the jury solution solved the problem with more than half of time limit. Why not for memory limit :( I am so sad.
I am getting wrong answer on the 5th test case. Not sure what I am missing. Could you please help?
I am using segment trees + lazy propagation for querying the maximum possible weight and d-value at an index and DP over these values.
Here's my code: 50479788. Help is very much appreciated. Thanks.
I believe there is a slight correction in the proof of C. bi and ci form a corresponding grouping only if the following condition holds:
bi = cj if and only if bj = ci.
The proof still holds because each grouping can be mapped to a bi, ci and the optimal bi, ci can be mapped to a grouping.
Fixed. I'm not sure if it is fine now. I'm a bit dizzy today. Wait a minute and the modification will be shown soon.
can you explain why my solution is incorrect,please 49283839
DFS is not suitable here. See this comment
Probably, in B, it should be O(n + m + MAXC) instead of O(n + m).
Did you use something called "bucket"? Actually it is not necessary to use that. A priority queue or a pointer is sufficient.
Could you please explain how the pointer leads to linear solution? Since dishes are not ordered by cost, we need to sort them first, right? It is already .
.
Oh ... I did make a mistake. I will modify this. Sorry for that.
In problem E , instead of the sweep line thing , i used a segment tree to cover the best red envelope in some range , and did the same Dp approach , however i'm still getting Wrong answer.
Any help would be appreciated , if my approach is wrong please let me know.
code : https://codeforces.net/contest/1106/submission/49283930
This is pretest 22 and the answer should be 2. However, you output 1.
Thanks for the test.
I read over and over my code and it looks just okay , so im starting to wonder if the approach is just wrong ..
Well I don't know how to use segment tree with the operator max, except that there is a technique called Segment Tree Beats. Hope you figure out your problem. :)
Before assigning a value to your lazy array you should check that you don't have a lazy value in your current node or that the value you want to put is better that your current lazy.
Something like this 49285040
Tried it but still not working :\
But thanks !
https://codeforces.net/contest/1106/submission/49289629 you meant me doing like that ?
UPD :
I got it accepted just after reading this blog : https://codeforces.net/blog/entry/57319
I highly recommend reading it , so beneficial !
Thank you jiry_2 !
Also thank you jinlifu1999 for mentioning the name of the trick !
Any test case for this Problem:D https://codeforces.net/contest/1106/submission/49285955
Try playing around with the following test:
Your solution will print
1 2 4 3which is not the correct answer.Can you tell the correct order
1 2 3 4
hey .. can you please tell why sorting doesn't work in this case
Because it doesn't care the path. At node v, you can go back to parent(v) and go to other nodes with smaller number.
In my opinion problem F is unreasonably hard for div2 (and not only to come up with a solution but also to implement)
My WA approach for E-
Sort all events Maximum Coins and then Maximum d.
Iterate on all events. I'm assigning a specific event for each moment, which I will select If not blocked and I can select an event.
Made dp states similar to editorial.
Took minimum of -
If blocked n-1(times),d-1(no of times blocked in i<n).
And If I can add specific event of ith moment in n-1,d then added or n-1,d.
Any specifice reason why does this fails?
To me both sweep and my approach look same.
Found reason why this approach will fail. :P
After that, we use a set with a sweep line to deal with it. — How ??
The transition is trivial and you can take a look at it in the code. — Not for me.
Please elaborate exactly what you are doing. And why you are updating
f[j & 1][a[i].d + 1]My solution for D is getting MLE. can someone help me? https://codeforces.net/contest/1106/submission/49291115
you shouldn't keep duplicates of vertices in a queue, so when vertex is visited don't push it to queue
https://codeforces.net/contest/1106/submission/49292899
Today I learned the big-step baby-step algorithm, and about primitive roots. Problems E and F are very interesting.
I'm sorry that this round faced technical difficulties, but I enjoyed it nonetheless.
Can someone explain why i am getting a "runtime error: constructor call on misaligned address" on problem E. Any help would be appreciated. https://codeforces.net/contest/1106/submission/49293426
The diagnostic message is not for your solution. Your solution gave a wrong answer that the checker wasn't prepared to handle, and the checker faced a runtime error. The diagnostic message is for the checker.
Your verdict is simply WA.
But the diagnostics mentions function<bool (std::pair<std::pair<int, int>, std::pair<int, int> > &, std::pair<std::pair<int, int>, std::pair<int, int> > &)> which i have used in my code.
I am very surprised to see that. I was certain that it might be due to the checker. But now I am not that sure.
One of the things that is curious is that you asked for GNU C++ compilation, but the diagnostic message mentions clang++ and MSVC. So that's suspicious indeed.
Please check once if your comparator is well defined.
Checked the comparator.Looks alright.
I think there might be something wrong with your solution, I copied it and changed it to this and no more exception but still wrong answer on test 7.
Figured already.I missed a condition in the DP part of code,which in no way could have caused byte misalignment.The diagnostic was incorrect. Thanks anyway.
Your defines are awful.
Can anyone explain the solution of problem E in detail,please ? The "SWEEP LINE" term mentioned in the editorial isn't clear to me.I understood the second part but i'm stuck with the first part. Thank you.
I'll try to explain, but my words might be unclear. Perhaps you could take a look at my submission. It might help.
What is dp[delayi + 1][rewardi]?
dp[delayi + 1][dist]?
Maybe dp[delayi + 1][dist] + rewardi?
Apologies. Thanks. Fixed.
I've corrected the error. Thanks for pointing it out.
I tried Problem E.
I let dp[i][j] be the coins Bob can obtain in time j with Alice already disturbed i times.
Let w[j] be the coin from the next envelope Bob can get if he is free at time j.
Let d[j] be the next time Bob can be free after getting this envelope.
then dp[m][j]=dp[m][d[j]]+w[j]
dp[i][j]=min(dp[i+1][j+1],dp[i][d[j]]+w[j])
But I got a Wrong Answer at test 5, which is very hard to find out the wrongs in my code.
I'll keep trying...
Please notice that f[ * ][m] might not be the optimal policy. Alice may not use all m chances to disturb Bob, which might reach a smaller answer.
Hi! It has been a long time, but if you could help me it'll be great. I don't get why my solution fails though the dp seems to be same as above.
https://codeforces.net/contest/1106/submission/157647999
Failing at TC 10. Seems to be some error in base condition. Don't get how.
See your output on TC 10. The answer could be larger than 2147483647, so initiate the answer to be some larger number instead of INT_MAX.
In 1106A,
scanf("%s", a[i] + 1);, whya[i]+1is used? Why it is needed to add 1 there?If you do not add 1, the variable j should start from 0.
There's something worthy to note about problem F that I came up with while testing. After reducing the problem to finding an integer x such that xp = m using matrix expo, we can find x in O(log(n)) but if and only if gcd(p, mod - 1) = 1. Let inv be the modular inverse of p with respect to mod - 1:
It was this line of thinking that led me in quite a wrong direction in the contest.
For the case where gcd(p, mod - 1) > 1, then we can reduce it to the case where p divides mod - 1 by the following steps:
Then,
Because mod - 1 has only three prime factors 2, 7 and 17, I was trying to find a special solution for those three powers, and entered into the number theory rabbit hole of quadratic residues.
Is there a way to solve the equation when gcd(p, mod-1) != 1 or this solution works only when gcd = 1?
Solution
Great, Thank you!
I also did the same thing mentioned in the editorial for B problem . Just used a set and simulated the process . I am getting a runtime error on the first case but in my local machine I am getting a right output . Can someone help me with the error ?
Link for the submission is : 49266362
At first I think D is very similar to NOIP2018 D2T1,but at last, it turns out that I am wrong.The code is same as the wrong code I wrote at NOIP2018.
same, took me a long time to find out that it is not NOIPD2T1 with extra edges :(
真的是两个中国人说话讲缨语
然后我也是D2T1写挂/px
Why am I getting runtime error on pretest 2 in Problem D? It is running fine on other online ide like gfg. https://codeforces.net/contest/1106/submission/49308034 Pls help!
Do not use set, use priority_queue instead, it will work fine. It's with the erase function of set which is showing undefined behavior. I also faced same issue.
Thanks buddy
Is there anyone who can explain the problem E in details? I'm trying to figure it out, but it doesn't work. I hope someone do me a favor please.
I understood what the problem requires, but I can't understand the way 1) calculating max coin 2) what structure you are using in calculating max coin (Why use map(set)?, what's the purpose of it?)
Because of my understandings, I also don't know about DP definition. After understanding the way above, I will try to understand DP approach.
Thanks in advance...
Perhaps you could take a look at my comment above.
Comment Link
For DP part you can look at proofbycontradiction's comment above.
We use map because we need to get the max event of each 'time' on timeline effectively.
Map is a balanced binary search tree, which means elements in it is sorted.
Therefore, we can get the max event(equals to the max coin) among all events in the tree by
cur.begin()->first.In order to calculate the max coin of every 'time' on the timeline effectively, we introduce two vector array
add[N]andremove[N]. At any 'time'i, if there're some events inadd[i], just insert them into the tree(map). If there're some events inremove[i], remove every of them from the tree.By doing this, it is guaranteed that at all 'time' i, for all events in the tree, the event's range includes i, and there doesn't exist such an event in the tree such that this event's range doesn't include i. Also, all events whose range includes i are in the tree.
When reading data from input, just
add[s].push_back(event),remove[t + 1].push_back(event). We uset + 1because s and t are inclusive, so you should remove it from tree at t + 1.You can calculate the max event of current 'time' during dp, or calculate them before dp. Both works.
Sorry for bad English, hope this helps! :D
Please correct me if there's any mistake, thanks!
I'd like to ask about C problem.
I came to know that we want to minimize sum bi * ci.
But, I can't know , why we sort ai(bi, ci), when we come to know we want to minimize sum bi * ci. Is there provement?
Here is the proof written by AwakeAnay
1: Groups must be formed as pairs of 2.
Proof: As (a+b)^2 > a^2 + b^2 for positive a, b, we want to minimize group size. As size has to be greater than 1, and N is even, all group sizes must be 2.
Now, we have to pair each number with another such that sum is least. We double this sum. This doubled sum can now be represented as summation (ai + bi)^2 where ai and bi are both permutations of the given numbers.
2: ai and bi must be oppositely ordered sequences
Proof: summation (ai + bi)^2 = summation (ai)^2 + summation (bi)^2 + summation (2*ai*bi); We want to minimize this sum. We observe that the first two terms are constants (sum of squares of all given numbers). So, we want to minimize the 3rd term. This is done when ai and bi are oppositely ordered, proof is a direct application of rearrangement inequality.
Now, observe that this doubled sum corresponds to the pairing where ai is paired with a(N-i+1), with i <= N/2. Thus, we are done
Thank you, ChevishaUchiha.
but, I'd like to know, why when we want to minimize sum a_i * b_i , we sort?
For example, a=(2, 3, 5, 7) we have to pair(2, 7), (3, 5). But I can't understand why is this correct?
Because you want to pair the largest one with the smallest one, next largest with next smallest, and so on. Since we are squaring each group having one group even slightly larger than it needs to be costs us much more than if we weren't squaring.
e.g. (2+7)^2+(3+5)^2 == 9^2+8^2 == 145
or try (7+3)^2+(5+2)^2 == 10^2+7^2 == 149
See how we have an average of 8.5 in the first example terms and 8.5 in the second example terms, but because we are squaring its much better to have terms 8 and 9 to square as opposed to 7 and 10 to square.
The terms have to be paired according to the question, makes no sense to make them groups of three or higher because every time you increase the square geometrically. So we know we are looking for pairs, and its best to keep the pair sums as close as possible.
Think 10 and 1 vs 5 and 6, both sum to 11, but their sum of squares 5 and 6 is 61 and sum of squares 10 and 1 is 101. Do that for any sum you can think of, you will see the closer they are the better.
Take 11:
10^2 + 1^2 == 101
9^2 + 2^2 == 85
8^2 + 3^2 == 73
7^2 + 4^2 == 65
6^2 + 5^2 == 61
So how do you take an array of numbers and make their pairs as close as possible? You sort them, two pointers, one in front i and one in back j. Sum and square front plus back, increment front, decrement back, while i<j.
I guess really it comes down to intuition, I don't have any hard mathematical proof that this gives you the closest pairs, but it feels that way.
Search for rearrangement inequality. It's simple to prove, intuitive and quite useful.
Basically, it states that if ai and bi are permutations of 2 sequences of real numbers, then the sum ai*bi will be minimized when ai and bi are oppositely sorted and will be maximized when they are similarly sorted.
Intuitively, if you want to purchase some items from a store, such that you want ai objects having price pi, then to minimize the total cost, you want to buy the costliest item as less times as possible and so on. So, if prices pi are increasing, then ai must be decreasing.
I understood the second proof by reading about proof og Rearrangement Inequality. But couldn't understand your proof for 1st part — having only groups of size 2. Can you please elaborate why only groups 2 will lead to optimal solution?
In the last part of problem F, there is no need to use extended euclidean algorithm to find a solution. Let's assume we want to find X such that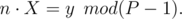
Such a number X exists only if y is divisible by gcd(n, p - 1). If yes, then we can reduce the fraction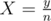 to
to 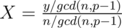 . Obviously now,
. Obviously now, 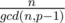 is invertible mod(P - 1) since they are co-prime, and n - 1 = nphi(p - 1) - 1
is invertible mod(P - 1) since they are co-prime, and n - 1 = nphi(p - 1) - 1
For problem E,which should be the times at which Alice will disturb for test 3? I can't find any combination in which he only gets 11 coins.
Bob collects 4 coins at time 1, collects 7 coins at time 6, Alice disturbs at time 11 and 12.
Can anybody explain how is answer for testcase3 = 11 for Div2E?
Bob collects 4 coins at time 1, collects 7 coins at time 6, Alice disturbs at time 11 and 12.
Thanks missed "after that" in statement :
If Bob chooses to collect the coins in the i-th red envelope, he can do it only in an integer point of time between si and ti, inclusive, and he can't collect any more envelopes until time di (inclusive) after that.
Can someone please help me fix my solution for problem E 49335045 I get WA on test 10
You shouldn't use LONG_MAX because LONG_MAX = 2 ^ 31 — 1. Try using 1e18.
UPD AC with #define LONG_MAX 1e18 — 49360125
Or use LLONG_MAX instead of LONG_MAX.
Thank you very much! I am new to c++ so this helped me a lot.
Hi, everybody! Please allow me to advertise my unofficial Chinese editorial of this round: Codeforces Round #536(Div.2)
For problem C, I think author's proof may be incomplete (or just lack of detailed explanations):
If bi and ci are settled, we can simply use Rearrangement Inequality to pair them.
But why must bi and ci be {a1, a3, a5, ..., an - 1} and {a2, a4, a6, ..., an} ?
My proof to this detail:
Any such pairing ({bi}, {ci}) can be "doubled" and be come a complete pairing between {ai} and {ai} .
For example: for
1 2 3 4 5 6, a pairing(3,1) (2,4) (5,6)can be seen asso a pairing can be represent as A , a complete pairing can be represent as B = f(A) (note that B = f(A) always exists but not A = f - 1(B)).
Then
Thus
cost(Ai) ≥ cost(A * )
Q.E.D.
For 1st part of problem E, how to include the condition for d(till when other envelopes can't be collected)?
In Problem F , Can anyone explain more about h_k ? and how can I obtain it from matrix exponentiation using linear recursive equation ?
Does problem F have a simpler solution?
Let's first say that f_i is a product of some powers of f1, f2,..., fk. This is true for all i.
We can then consider the recurrence as an additive recurrence over k dimensional vectors f_i = b1*f_i-1 +... +bk*f_i-k. We are basically considering a "logarithmized" version of the recurrence.
Then we can have a transition matrix M of size k x k to get from f_i, f_i+1,...,f_i+k to f_i+k+1,f_i+k+2,...,f_i+2k.
We then use fast exponentiation with matrix multiplication to get from f1...fk to fn (mod p-1 for values). The result will be that we will have fn expressed as a product of powers of f1...fk. We will use again fast exponentiation on numbers now to compute the values for the powers of f1..fk-1. We multiply fn by the inverse of this product and we get fk^b = a (mod p). Finally we are left with just computing the b-th root of a (mod p).
Final complexity should be O(k^3*log n + finding discrete b-th root).
Does this make any sense to you?
LATER EDIT: I just realized that this is more or less what the Tutorial also proposed.
Hi,can you tell me the test of 7 on Problem B? i wrong answer on it long time
In this equation, the mod number is 998244352 which doesn't have primitive root. You can't optimize it with NTT. I think the fastest solution should be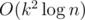 instead of
instead of 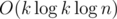 .
.
In fact, for arbitrary modulus (not very large) NTT, there is a trick called three-modulus-NTT (translated from Chinese). Suppose that we want to get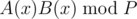 . The intuition is that the coefficients for the answer polynomial C(x) = A(x)B(x) won't exceed nP2, where n is
. The intuition is that the coefficients for the answer polynomial C(x) = A(x)B(x) won't exceed nP2, where n is 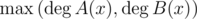 . Thus we choose 3 NTT-friendly modulus (whose multiplication is greater than nP2) to get the results and apply Chinese Reminder Theorem to retrieve the original answer back. The details can be found in some Chinese blogs (I'm sorry that I haven't found any in English).
. Thus we choose 3 NTT-friendly modulus (whose multiplication is greater than nP2) to get the results and apply Chinese Reminder Theorem to retrieve the original answer back. The details can be found in some Chinese blogs (I'm sorry that I haven't found any in English).
I got what you mean, but I have a question bro. As well as I know about the trick using NTT that you mention it's alright (you can obtain the convolution for any modulo), but when you use NTT to solve the lineal recurrence, at some point you need the rest of the division of two polinomials. Well if its true, to get the rest you need the division of two polinomials (quotient), and to obtain the quotient its necesary that the first term of one of the reverted polinomials have to have inverse. So, if your modulo its not prime, then you have a problem because there is not necessarily inverse for all numbers. So, I think what MAOoo_Love_Molly said its alright. Am I missing something? correct me if I'm wrong bro, I would really apreciate it.
The idea is that we can get rid of this "disgusting" number $$$P = 998244352$$$ and use 3 NTT friendly numbers (primes) to solve this problem. As is easy to check, if two polynomials of degree no greater than $$$n$$$ have coefficients no greater than $$$P$$$, then the coefficients of the multiplication of these two polynomials will not exceed $$$nP^2$$$. In this way, if we choose 3 NTT friendly primes $$$Q_1, Q_2, Q_3$$$ such that $$$Q_1Q_2Q_3 > nP^2$$$, we can uniquely recover the coefficients with modulus $$$P$$$ by Chinese Reminder Theorem. In this way we apply NTT with NTT friendly primes. Should you have any questions, I would be happy if you could send me an email to discuss it. Hope you find this useful :)
first at all, thanks a lot for reply bro!
Yes, as I said in my last comend, I know how to obtain the convolution for two polinomials for any arbitrary modulus. Well, my question was about how to obtain the lineal recurrence for any modulo (to get the complexity of O(Klog(K)log(n)). I mean, at some point you need the division of two polinomials, well and for this, one of them, have to have inverse, but with any arbitrary modulo, is it possible? I mean, at some point you need the inverse modular of a number, and as far as I know it doesn't necesary exists for any modulo.
Sorry for my bad english.
Do you know the standard solution with complexity $$$O(k^2 \log n)$$$? This approach is simply by multiplication of polynomials for $$$O(\log n)$$$ times. We aim to optimize the multiplication to $$$O(k \log k)$$$, and this is what I am talking about in the previous comment. :) Feel free to comment if you have further questions.
It seems that the above approach is wrong.
Thanks for giving me such a reminder ... I checked the method of solving the linear recurrent equation and found that we do need the inverse of a polynomial. Then I am not sure if this works. Sorry for that inconvenience and you are right :) If you find any approach to this problem I will be looking forward to seeing it. Thanks again!
I think maybe the complexity of BSGS could be reduced to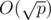 .
.
In number-theory part, if we search for an x satisfying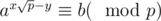 instead of
instead of 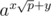 , we have
, we have 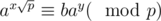 , so we don't need to get inversion modulo p which takes
, so we don't need to get inversion modulo p which takes 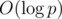 time.
time.
In data-structure part, maybe we can use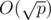 (although I have never implemented it before)
(although I have never implemented it before)
unordered-mapinstead of map, then the total complexity isCould someone explain why in problem D sorting all the adjacency list and then using Dfs as it will always traverse the lowest nodes first gets a wrong answer? here is my code https://codeforces.net/contest/1106/submission/53541920
You will understand your mistake if you try this case
The mistake is we do not want to specifically use dfs or bfs, just a pq will do.
Can anyone please explain how the state has been reduced in problem E.
For problem D, why I am getting wrong answer? Can any one please find out the error? thanks in advance._. 257438260