guest666's blog

Square Root function gives 4 decimal places precision only?
By guest666, history, 5 years ago, In English

Hello there. I have experienced an unexpected problem when calculating square root of a function. I used sqrtl(number+EPS) and I expected it to pass system testing in today's problem B. My equation was a quadratic equation and it should've passed. 74435525 this is my submission. I've found that the sqrtl() only calculated to 4 decimal places precision. I expected it to be more precised. I am not sure why the precision was very inaccurate?(In the hack, I got wrong answer due to precision error). I googled my problem before asking here. I also used __float128 in custom invocation tab with 64 bit C++ with my custom square root function using binary search and still, it wasn't accurate. The testcase that made me fail:

1

36000 600000000

  • Vote: I like it
  • +2
  • Vote: I do not like it

»
5 years ago, # |
  Vote: I like it +12 Vote: I do not like it

The square root function is very accurate. It will usually have much more than 4 decimal places of precision unless used with large numbers, in which case the issue is just the floating point format.

I also checked your example test case and the value of quadratic is definitely correct for way more than 4 decimal digits. It is the only place where you use square root.

What prompted you to assume the issue is in sqrt precision? Can you show some actual evidence?

→ Reply
  • »
    »
    5 years ago, # ^ |
      Vote: I like it -12 Vote: I do not like it

    That was the test I made in custom test tab. I am making (sqrtl(4800000001)-1)/2 And here are the results: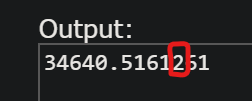

    The sad fact that this 2 must actually be a 5. I've checked it with my Casio calculator. I also checked that (34640.5161251)*(34641.5161251) didn't give 1200000000 as expected. It gave: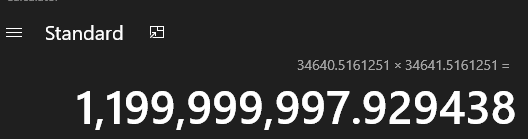

    → Reply
    • »
      »
      »
      5 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      That's because you're computing (sqrtl(4799999993)-1)/2 instead. I haven't read the problem and haven't tried to understand your solution, but you reduce $$$b$$$ by 1 on line 15. The answer you get is precisely what it should be.

      → Reply
      • »
        »
        »
        »
        5 years ago, # ^ |
          Vote: I like it +3 Vote: I do not like it

        My bad, you are right. Sorry for that. Anyways, the accurate answer that it gave me before I multiply: 34640.5161261184715826 You are right! It gives an accurate answer. But how much does the error increase when I multiply the number with its self? I got accepted after I removed the multiplication by quadratic*(qudratic+1) as it means that I am getting the value of B. 74549911 got accepted when I didn't multiply the quadratic*(quadratic+1). I guess this is due to that floating point has a small error and multiplying by its self increases this error. But how much error does it increase?

        → Reply
        • »
          »
          »
          »
          »
          5 years ago, # ^ |
            Vote: I like it +4 Vote: I do not like it

          Quantifying bounds on errors is a whole branch of in itself. I won't get into it as I don't think that's the case here.

          Your value of quadratic*(quadratic+1) will always be at least a little bit inaccurate because it's floats. You convert to int so if it is even slightly smaller than the exact value it will be one less.

          Now you've tried to tackle the problem by adding an epsilon, but your epsilon is absurdly small. It is so small that I am not even sure if it is even parsed as anything different from 0. Here is a submission where I just increase your epsilon and it works — 74552069. Since you know you're looking for an exact value, a round would be even better — 74552594.

          → Reply
          • »
            »
            »
            »
            »
            »
            5 years ago, # ^ |
              Vote: I like it +13 Vote: I do not like it

            Thank you very much sir! I really appreciate your tips!

            → Reply