BinaryCrazy's blog

Request for help on DP / Math Problem
By BinaryCrazy, history, 5 years ago, In English

Hi all,

Hope you are all safe with the unfortunate events occurring throughout the world.

I was solving some problems on HackerEarth's CodeArena platform (1v1 other person, 1 problem, 20 mins, who ever gets more TCs wins) , when I came across this problem (the contest has ended). I have attached the screenshot of the statement to this post.

I first attempted to use combinatorics and math to solve it, but later changed to applying DP. However, I couldn't figure out a recurrence between the states (# of objects, # of groups).

I would really appreciate it if someone could lend a helping hand with the recurrence. Also, IF there is an easy mathematical solution to the problem, please share it.

Thanks for your help and time! BC

EDIT: Sorry, I assumed that the 'Add Image' feature automatically appended the image to the post. Attached below is the image.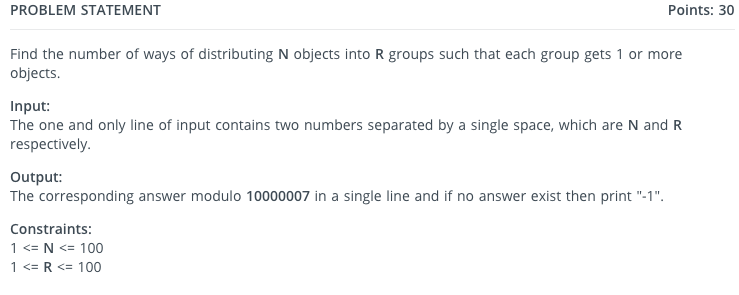

Sample TC: Input: 4 2

Output 3

  • Vote: I like it
  • +4
  • Vote: I do not like it

Comments Comments (12)
| Write comment?
»
5 years ago, # |
← Rev. 4   Vote: I like it 0 Vote: I do not like it

DP[i][j] = #of ways to put 'i' objects given 'j' open groups.

You have 2 transitions:

  1. Add the current object to an open group — DP[i + 1][j] += j * DP[i][j]

  2. Create a new group — DP[i + 1][j + 1] += DP[i][j]

Answer is DP[N][R]

→ Reply
  • »
    »
    5 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Wouldn't transition 2 be DP[i][j.+ 1] += DP[i][j]?

    You do not add an object every time you create a group?

    → Reply
    • »
      »
      »
      5 years ago, # ^ |
      ← Rev. 2   Vote: I like it 0 Vote: I do not like it

      How can you have a group without an object?

      → Reply
      • »
        »
        »
        »
        5 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        I like to pretend this is some philosophical question. "But how can there be a group if there is no object"?

        → Reply
        • »
          »
          »
          »
          »
          5 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          My username also poses an interesting philosophical question: "Is water wet?"

          → Reply
      • »
        »
        »
        »
        5 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        But, Mr. wet_water, adding an object isn't a necessary requirement for creating a group!

        → Reply
        • »
          »
          »
          »
          »
          5 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          Can you read the problem again, it says that each group must have at least 1 person

          → Reply
»
5 years ago, # |
  Vote: I like it +8 Vote: I do not like it

I think this is a classic stars and bars problem, you can read an introduction of that here. https://cp-algorithms.com/combinatorics/stars_and_bars.html

→ Reply
»
5 years ago, # |
← Rev. 4   Vote: I like it 0 Vote: I do not like it

The problem can be easily solved with a simple recursive DP that works in O(N*R). Here is the code: https://ideone.com/c0Hjq2

Explanation: First, lets fill all the DP array values' to -1. Start a recursive function that has two parameters x y for example. Let x be the index of N. Let y be the objects that are currently available. If y is less than 0, then there is no answer. So return 0.(We are building up in this type of DP). But if x reached n, and y is equal to 0, then the job is done and it successfully distributed all of its objects so it return 1. Otherwise, if x reached n and y isn't equal to 0, then it didn't finish its objects so it returns 0. We will run a for loop from 1 to y and try and distribute 1 object to the current group we are one, 2 objects to the current group we are on, 3,4,... until y. We will subtract what was taken from the objects and run that recursive.

Edit: Found a combination solution which is: (N-1)C(R-1)(C means combination) But notice that: You cannot divide a number with modulo. You can read more about it: Here

→ Reply
»
5 years ago, # |
  Vote: I like it 0 Vote: I do not like it

dp[i][j]->total number of ways to group i numbers of objects in j number of groups.

There are two possibilities either we create a new group or don't create a new group so the recurrence relation will look like this....

dp[i][j]=dp[i-1][j-1]+j*dp[i-1][j]

→ Reply
»
5 years ago, # |
  Vote: I like it +9 Vote: I do not like it

it is simply (n-1)C(r-1).

→ Reply
»
5 years ago, # |
← Rev. 4   Vote: I like it +1 Vote: I do not like it

The question is a bit vague. When are two ways considered different? Are the groups differentiable. If yes then the solution is the coefficient of x^n in (x+x^2+x^3+...+x^n)*(x+x^2+x^3+...+x^n)*... r times (since there are r groups and we have to distribute total n items, also the power of x starts from 1 because we have to select atleast 1 item for a group). So,

coefficient of x^n in (x+x^2+x^3+...+x^n)*(x+x^2+x^3+...+x^n)*... r times

=>coefficient of x^n in x^r*(1++x+x^2+x^3+...+x^(n-1))*(1+x+x^2+x^3+...+x^(n-1))*... r times

=>coefficient of x^(n-r) in (1+x+x^2+x^3+...+x^(n-1))*(1+x+x^2+x^3+...+x^(n-1))*... r times

=>coefficient of x^(n-r) in (1-x)^(-1)*(1-x)^(-1)*... r times

=>coefficient of x^(n-r) in (1-x)^(-r)

=>(r+n-r-1)C(n-r)

=>(n-1)C(n-r)

=>(n-1)C(r-1) (since nCr = nC(n-r))

This can also be solved using dp. The state is dp[i][g], where dp[i][g] is the solution for the subproblem items [i:n-1] with g groups remaining. So the final solution is dp[0][r] or solve(0, r). A recursive method would look like:

       private static int solve(int i, int g) {
		if (i==n) {
			if (g==0) return 1;
			else return 0;
		}
		if (g==0) return 0;
		
		return solve(i+1, g-1)+solve(i+1, g);
	}
→ Reply