Codeforces round #716 editorial

#	User	Rating
1	tourist	4009
2	jiangly	3823
3	Benq	3738
4	Radewoosh	3633
5	jqdai0815	3620
6	orzdevinwang	3529
7	ecnerwala	3446
8	Um_nik	3396
9	ksun48	3390
10	gamegame	3386

#	User	Contrib.
1	cry	167
2	Um_nik	163
3	maomao90	162
3	atcoder_official	162
5	adamant	159
6	-is-this-fft-	158
7	awoo	157
8	TheScrasse	154
9	Dominater069	153
9	nor	153

1514A - Perfectly Imperfect Array

If any element is not a perfect square, the answer is yes. Otherwise, the answer is no, because $$$a^2*b^2*...=(a*b*...)^2$$$.

Code link: https://pastebin.com/s83sFt3G

1514B - AND 0, Sum Big

Let's start with an array where every single bit in every single element is $$$1$$$. It clearly doesn't have bitwise-and equal to $$$0$$$, so for each bit, we need to turn it off (make it $$$0$$$) in at least one of the elements. However, we can't turn it off in more than one element, since the sum would then decrease for no reason. So for every bit, we should choose exactly one element and turn it off there. Since there are $$$k$$$ bits and $$$n$$$ elements, the answer is just $$$n^k$$$.

Code link: https://pastebin.com/0D8yL5WW

1514C - Product 1 Modulo N

So first observe that the subsequence can't contain any element that isn't coprime with $$$n$$$. Why? Because then its product won't be coprime with $$$n$$$, so when you take it modulo $$$n$$$, it can't be $$$1$$$. In mathier words, $$$gcd(prod \space mod \space n,n)=gcd(prod,n) \neq 1$$$. Now, let's take all elements less than $$$n$$$ and coprime with it, and let's look at their product modulo $$$n$$$; call it $$$p$$$. If $$$p$$$ is $$$1$$$, you can take all these elements. Otherwise, you should take them all except for $$$p$$$. It belongs to them because $$$p$$$ is coprime with $$$n$$$, since $$$gcd(p \space mod \space n,n)=gcd(p,n)=1$$$ since all the elements in $$$p$$$ are coprime with $$$n$$$.

Code link: https://pastebin.com/JnjZ3SQm

Bonus task: solve it for $$$n \le 10^{12}$$$.

1514D - Cut and Stick

Suppose the query-interval has length $$$m$$$. Let's call an element super-frequent if it occurs more than $$$\lceil\frac{m}{2}\rceil$$$ times in it, with frequency $$$f$$$. If there's no super-frequent element, then we can just put all the elements in $$$1$$$ subsequence. Otherwise, we need the partitioning. Let's call the rest of the elements (other than the super-frequent one) good elements. One way to partition is to put all the $$$m-f$$$ good elements with $$$m-f+1$$$ super-frequent elements; then, put every remaining occurrence of the super-frequent element in a subsequence on its own. The number of subsequences we need here is then $$$1+f-(m-f+1)=2*f-m$$$. There's no way to improve this, because: for every subsequence we add, the number of occurrences of the super-frequent element minus the number of good elements is at most $$$1$$$, so by making it exactly $$$1$$$ in each subsequence, we get an optimal construction. Now, the problem boils down to calculating $$$f$$$. Note that calculating the most frequent element in general is a well-known slow problem. It's usually solved with MO's algorithm in $$$O(n\sqrt{n}log(n))$$$, maybe with a tricky optimization to $$$O(n\sqrt{n})$$$. However, notice that we only need the most frequent element if it occurs more than $$$\lceil\frac{m}{2}\rceil$$$ times. How can we use this fact?

Randomized solution

We can pick ~$$$40$$$ random elements from our range to be candidates for the super-frequent element, then count their occurrences and maximize. If there's a super-frequent element, the probability it's not picked is at most $$$2^{-40}$$$, which is incredibly small.

To count the number of occurrences of an element in a range, we can carry for each element a vector containing all the positions it occurs in increasing order. Then, upper_bound(r)-lower_bound(l) gives us the number of occurrences in $$$O(log(n))$$$.

Code link: https://pastebin.com/APHEtfge

Deterministic solution

Observe that if a range has a super-frequent element, and we split it into $$$2$$$ ranges, then this element must be super-frequent in one of them. Now suppose we create a segment tree where every node $$$[l;r]$$$ returns an element in the range, and suppose every node merges the $$$2$$$ elements returned by its children as follows: count their occurrences in $$$[l;r]$$$ and pick whichever occurs more. In general, that doesn't return the most frequent element. However, if there's a super-frequent element, it must return it! That's because if there's a super-frequent element in $$$[l;r]$$$, it must be super-frequent in one of its children, so by induction the segment tree works. The time complexity is $$$O(nlog^2(n))$$$.

Code link: https://pastebin.com/qeGxT0W2

There are also tons of $$$O(n\sqrt{n})$$$ solutions that should pass if the operations are simple enough.

Bonus task: solve it in $$$O(nlog(n))$$$.

1514E - Baby Ehab's Hyper Apartment

Throughout the editorial, I'll call the first type of queries OneEdge and the second type ManyEdges.

The basic idea behind this problem is to find a few edges such that every path that could be traversed in your graph could be traversed using only these edges. With that motivation in mind, let's get started.

The first observation is: the graph has a hamiltonian path. To prove this, suppose you split the graph into $$$2$$$ halves, each containing some of the nodes. Then, we'll proceed by induction. Suppose each half has a hamiltonian path. I'll describe a way to merge them into one path. First, let's look at the first node in each path and ask about the edge between them. Suppose it's directed from the first to the second one. Then, I'll start my new merged path with the first node, remove it, and repeat. This works because no matter which node follows it, it sends an edge out to it. This is best described by the following picture:

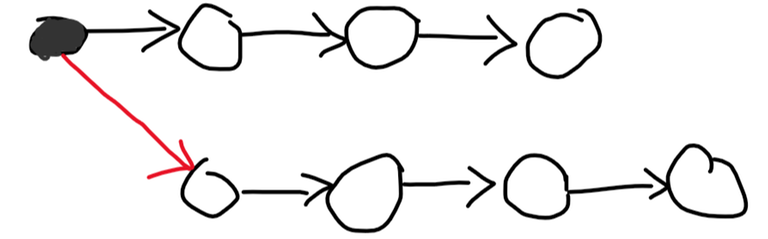
We start with the $$$2$$$ hamiltonian paths we got by induction, then we query that red edge. We find that it's from the grey node to the white node. We then put our grey node as the start of the path and continue doing that with the rest of the nodes, and we don't care which node will follow it, because the edge is out from the black node either way!

If everything falls into place in your mind, you should recognize that this algorithm is merge sort. We just run merge sort on the nodes of the graph, using the comparator OneEdge. That gives you a hamiltonian path in $$$nlog(n)$$$ queries.

Now that we have a hamiltonian path, every edge that goes forward in it is useless, since you can just walk down the path itself:

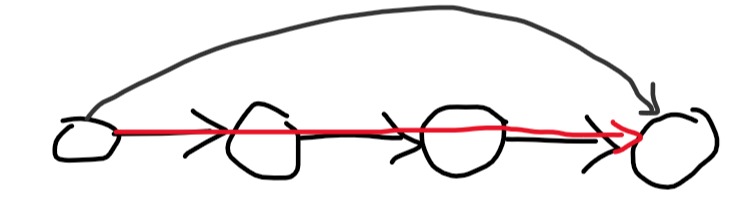
So let's focus on the edges going backwards. Suppose we iterate through the hamiltonian path from its end to its beginning, looking at the edges going back from the nodes we met. An edge going backwards from the current node is important only if it goes back further than any of the edges we've met so far. That's because we can take a (much less direct) route instead of this edge if it doesn't go so far back:

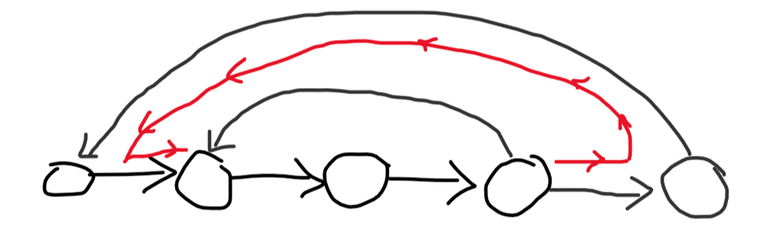
Now with a few more edges we can form all the paths! How do we get these edges? We can use $$$2$$$ pointers. Let's iterate through the hamiltonian path from its end to its beginning, carrying a pointer $$$p$$$ that tells us how far back the edges we met so far can go. To update $$$p$$$, let's ask ManyEdges from the node we're currently at, to the first $$$p$$$ nodes in the hamiltonian path. While the answer is $$$1$$$, we'll keep decreasing $$$p$$$. This algorithm calls ManyEdges $$$2n$$$ times, since every time we call it, it either returns $$$0$$$ and the node we're at decreases, or it returns $$$1$$$ and $$$p$$$ decreases.

Code link: https://pastebin.com/RU1yA697

Bonus task: can you get the hamiltonian path using insertion sort instead?

(a * b) % n = k * n + r => (a * b) % n = g * (k * n / g + r / g) [here, g = gcd(n, r)] => (a * b) % n = g * (some_number) Also, since (a * b) % n = (a % n) * (b % n) => (a % n) * (b % n) = g * (some_number) Since both a and b are less than n here, => a * b = g * (some_number)

Comments (222)

Show archived | Write comment?

skittles1412

4 years ago, # |

+268

google forces

→ Reply

SergiuS2003

4 years ago, # ^ |

-27

It's hard to propose some "never seen before" problems, especially because they can't check if the problem they proposed is somewhere on the internet.

+92

https://www.google.com/search?q=product+1+modulo+N

The exact name of the problem...

Finding range most frequent just requires a bit more searches.

Yes, you're right. It's too much of a coincidence, I haven't noticed the name.

dr.stone

+144

NO wander antontrygubO_o rejected all the problems

CoderAnshu

-96

Btw in D the constraints could have been increased so that only randomized solutions work.

mohammedehab2002

+120

Easier said than done. $$$40log(n)$$$ and $$$\sqrt{n}$$$ are incredibly close for any practical $$$n$$$ for programming.

WeakestTopology

← Rev. 2 →

+68

Maybe forcing the queries to be answered online would've been a good option here.

+59

You're right. I don't know how it didn't cross my mind :(

Ohh great!!

magnus.hegdahl

+18

I solved it with square root decomposition online here.

Online is not enough to force randomization.

arujbansal

+19

We can still use a basic segment tree to solve it in Q.log(N) even if online is forced 113593731

For C, I don't see how this link helps. You don't use this idea to solve the given task; you use it to optimize the solution and solve the bonus task, for example. This link is supposed to be helpful after you get the idea of using the numbers relatively prime to $$$n$$$, but then the remaining part (removing $$$p$$$ if it's not $$$1$$$) is really easy and shouldn't need the link or anything.

For D, I tried my best to fail the solutions based on MO's algorithm or any idea that solves the most frequent element problem in general, without using the fact that it has to be super-frequent. It sucks that some still passed...

+22

For C you can see that the product is either 1 or n - 1 (as shown by the link). We see that n - 1 is always coprime to n, so we can just remove it if necessary.

For D the randomized solution is really cool, and it's quite unfortunate that MO's was able to pass. Although it is hard to block out efficient MO's solutions and keep slower randomized solutions, n not being too high (only 3e5 as opposed to something like 1e6) and the TL being 3s was enough to suggest that MOs was worth a try.

adam_rajsky

Unless you force answering online, blocking MO is not really possible — my MO solution ran in 850 ms.

+24

Without forcing answering online, you could increase n and decrease q to pass the randomized solutions while blocking MO's. For example n being 2e6 and q being 5e4 should let the randomized solutions pass while blocking MO's with some special test cases.

arman.t

Can you link to your solution, please?

krm24

Hey I had a doubt in Problem D (MO's Algo solution):
Why this 113542641 took only 717ms while this 113538699 gave TLE. It's my mistake that I bluntly copied. But I don't understand why there's so much difference when the loop is going to end just after one iteration.

Turkey

you should check whether "t_ans <= 0",otherwise it would be out of bound of array

Shouldn't it give run time error? Correct me if I am wrong t_ans is the freq of the most frequent element so during mos algorithm when the left pointer would be in the right of the right pointer the t_ans would be negative.

When t_ans is negative it may access the wrong location, such as the end of "a" , and then it will perform the "t_ans --" operation many times leading to a timeout, which sometimes does not return RE. And you can adjust the order of transformations of l and r in Mo's algorithm so that l > r never exists.

By end of "a" do you mean the end of the counter array? I looked it up online and found negative indexes are not instantly detected by c++. This makes sense now.
while(current right pointer < query[i].right) add(a[++r]); This should be placed executed before all other transformations so that l > r never exists.Thanks for helping!

Graphter

If you had made the queries to be solved online, wouldn't you have blocked the MO's solutions ?

kshitij_sodani

+12

I think the super-frequent idea is also well-know.I remember seeing it atleast 2-3 times before(like POI 14-Couriers)

Xhnxhn

← Rev. 3 →

I use MO's algorithm to solve this problem in O(q*sqrt(n)) 113568653

dedsec_29

But you're also doing a binary search before calculating final answer for a query if I am not wrong, so shouldn't there be an additional log(n) factor?

Yes，you are right，The time complexity of the algorithm is(q*sqrt(n)+q*log(n)), but when N is large,the q*log(n) can be ignored.

vrishinvv

← Rev. 8 →

what exactly are you binary searching on? edit1: nvm understood! thank you :)

Thallium54

also

Breaker-iwnL-

+35

for me it was guessForces

mcGyver

it's really sad. now i realize how C got so many solve

kira201

+23

In B's solution,there is a typo, answer should be n^k

FenWick

← Rev. 4 →

Pab007

what will be the max sum is this case I constructed the array such that the max sum is (n-1)(2^k-1) :n-1 elements are 2^k-1 and one element is 0 :n-2 elements are 2^k-1 and one element is 1 and other is 2^k-2 :n-2 elements re 2^k-1 and one element is 2 and 2^k-3 and so on maintning the sum (n-1)(2^k-1) is this approach wrong

I did think like u, but after simulating the process. I got n^k(

beingsebi

For D, can't we get O(n * log(n)) using wavelet trees?

C20200522

You can use persistent segment trees and binary search to get O(n*log(n)), because there's at most one value to occer more than ⌈x/2⌉ times, and you just need to find it.

suhail.loya

I think you meant n^k in Problem B

Sportsman

Weird, the below code (for problem A) is giving one output for my compiler and another for codeforces one. Can someone tell why?

Spoiler

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long int ull;
#include <fstream>
//#define int long long int
#define mod 1000000007
#define watch(x) cout<<(#x)<<" is "<<(x)<<"\n"
#define watch2(x,y) cout<<(#x)<<" is "<<(x)<<" and "<<(#y)<< " is " <<(y)<<"\n"

int main(){
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);
    int t=1;
    cin>>t;
    while(t--){
        int n;
        cin>>n;
        int a[n];for(int i=0;i<n;++i)cin>>a[i];
        int flag = 0;
        for(int i=0;i<n;++i){
            if(sqrt(a[i])*sqrt(a[i])!=a[i]){
                flag = 1;break;
            }
        }
        if(flag)cout<<"YES"<<endl;
        else cout<<"NO"<<endl;
    }
    return 0;
}

Ritwin

-9

Probably floating point errors, see the if(sqrt(a[i])*sqrt(a[i])!=a[i]){ line, you're dealing with floating point numbers.

nagabhushan

In D, I picked 20 random numbers. Not sure if it will pass the main tests.

Ahmadsm2005

Lets say there are a 100 tests each with $$$3*10^5$$$ queries.

Therefore, expected number of failure: $$$\frac{3*10^7}{2^{20}}$$$

which is sadly large. Unless you are lucky enough.

Yeah did the same analysis. Tried increasing the random number to 30, but got TLE. May be the way I wrote the code was inefficient.

I guess the bottleneck is from Java its self :/ I joined Egyptian IOI TST and was able to set it to 60 random numbers without timing out.

rohit_goyal

35 is a good number, you should pick it so that (1 — 0.5^k)^(30000000) >= 0.999.

175iq

Can someone please explain C more ?

ThoughtNerd

very nice editorial.The randomized solution of problem D is nice.

DIVANSHMAHAJAN29

can someone explain soln of c If p is 1, you can take all these elements. Otherwise, you should take them all except for p. It belongs to them because p is coprime with n. what does this mean?

codefforces

If $$$\{x_1,x_2,...\}$$$ is the set of all integers coprime with $$$n$$$ (and less than $$$n$$$), then the product $$$q=x_1\cdot x_2\cdot...$$$ is also coprime with $$$n$$$. Therefore $$$p = q \mod n$$$ is coprime with $$$n$$$. (These can be proved using the definition of coprimality.) This further means that $$$p=x_i$$$ for some $$$i$$$. So we can exclude $$$x_i$$$ so that the product $$$x_1\cdot...x_{i-1}\cdot x_{i+1}...$$$ now equals 1 modulo $$$n$$$. No need to exclude $$$x_i$$$ if $$$x_i=1$$$.

Thanks a ton bro

Thank you, this pointed me to the right direction. I was still unsure about the guarantee that p is coprime with n, but the accepted answer here showed me why.

Qassim

3 years ago, # ^ |

Can you please tell me why "This further means that p=xi for some i." ? why must p be included in the set ?

By definition, the set contains all the coprimes, so it must contain $$$p$$$ as well.

JEEADVANCED

+10

This Contest Goes too bad for those who don't know how to search on google while contest is running.

dabbingpony

+70

No XOR problems :(

d-agrawal

In problem C editorial, it is written:

Because then its product won't be coprime with n, so when you take it modulo n, it can't be 1.

What is the reason/ proof for this statement?

I figured it out. Let the product formed be p. If a non co-prime number is in p, since p has a common factor witn n, it is of the form k*n, which can never be m*n + 1.

So, all numbers must be co-prime with n

distroter

if n=4. and sequence is {1,2,3} then p = 6 which is not of the form k*n. Not sure what you deduced is coreect

Muhammad_mhs

Lets, product is P then gcd ( P , n ) != 1 that is P and n must have a common factor. Imagine there is X axis from 1 to (inf).

Assume, P = 8 and n = 6 then

Common factor between P and n is 2.

so, P = 2*4 and n = 2*3.

put them point as X axis. then you see that mod must be a multiple of common factor where smallest possible mod is a common factor of P and n( here 2 ). So, if you take a non co-prime number in product there is no possibilities to get P%n = 1.

Kofta

Why mod must be a multiple of common factor?

pasthec

Because otherwise you would have $$$p = kn + 1$$$ for some $$$k$$$ so $$$GCD(p,n)=1$$$ by Bezout's theorem and $$$p$$$ is coprime with $$$n$$$.

0verHaul

I never heard about that theorem can you please tell me which theorems should I learn in number theory for competitve programming basis .

coder_Aditya_404

i guess by doing tons of questions :)

That was really helpful :(

lol

I think you should look at any basic number theory course that goes at least up to euler's indicator and chinese remainder theorem, it should include most of what you need. If you want to go deeper knowing group theory is great for better understanding but otherwise just do whatever seems fun to you.

yeah thanks but wouldn't cp algorithms website is enough?

cp-algorithms teach you the algorithms, not the theory (here for instance it won't teach you bezout's theorem)

oh okay, will look into it. it will be good if u can point any(link).

Thanks a lot :joined_hands.

wouldn't*

$$$gcd(p \space mod \space n,n)=gcd(p,n)=1$$$ since every element in $$$p$$$ is coprime with $$$n$$$.

Ok lets say you took some no. which is not co-prime with n in p then they would have a common factor say m, now we can express p and n as

p = m*a

n = m*b

for arbitrary a,b (which are co-prime to each other)

and now for getting (p mod n) = 1 ,we should have p = k*n + 1 and if we substitute values of p and n from our equations we have.

m*a = k*m*b + 1 but clearly the rhs is not multiple of 'm' which is contradiction.hence p should have all no.'s which are co-prime with n.

hope it helps :)

PR_0202

I did B,C,D without any proof purely by guessing xD

wannabeGM

Intuition 100

anirudh31

can someone explain B why answer is n^k ?

_reevu_lmao_ktksan_

Since we have to make the sum as large as possible while keeping their bitwise AND to be 0, we observe that we can do this by setting each bit from 0 to k-1 in exactly (N-1) of the numbers. It's easy to see that the bitwise AND of this comes out to be exactly 0, while the sum remains as large as possible(can be proved by contradiction). Now, we have to assign these k bits to (N-1) of these numbers so, the total number of ways for each bit will be N choose N-1 which is N. Hence, for k bits, it would be N^k.

Mohammed2002

For the first bit in all the $$$n$$$ numbers (which all their bits are initially $$$1$$$) , you have to make exactly one bit to be equal to $$$0$$$ and you have $$$n$$$ choices for that , and the same for the second bit .. up to the $$$k-th$$$ bit , so it becomes $$$n * n * n ... * n $$$ k times, which is obviously $$$n ^ k$$$.

In problem B its N^K i guess not K^N Fix it

Fixed. Thanks!

what is the max sum that can be achieved

(2^k-1)*(n-1)

can we build the array like this - 1:_ 0 +(n-1)*(2^k-1)_ - 2: 1 + 2^k-2 +(n-2)(2*k-1) - 3:_ 2 + 2^k-3 +(n-2)(2*k-1)_- and so on maintaining the sum n-1*(2^k-1) and BITWISE AND 0 what is wrong in this

Nzht

In problem B, how are we sure that we have to have at least 1 zero and the rest will be greater than 0. For example, what if we had

n = 3, k = 4 and max_possible_sum = 2^k * (n-1) => 32 (assuming that the array will be like this -> {0, 16, 16}) in this case, can the array be also like this -> {2, 4, 26} cause the total sum is 32 and the whole AND of the array is still 0. But we didn't use any 0 to get the maximum sum.

{0,16,16} is invalid for k=4 because 2^k — 1 = 15.

mon0pole

max possible sum is (2^k — 1)*(n-1) and you can't take 16 if k=4
the max value of any element can be 15 (for k=4)

del1ke

In problem B the answer is n^k (or pow(n,k)) with mod 10e9+7, fix your mistake please

Can we find the most frequent element using persistent segment tree?

pied-piper

-8

TheeLooser

+127

Bonus of D: Deterministic $$$O(q \log n)$$$.

Consider this problem: there is a hidden array $$$a_1, a_2, a_3, \ldots, a_n$$$. You have to figure out if there is any number more than half of the times. You can only compare two elements $$$i$$$ and $$$j$$$- if they are equal or not.

One possible solution of this is: maintain a stack and try to push every element into the stack in this order: $$$a_1, a_2, \ldots, a_n$$$. When you try to push $$$a_i$$$, if the top element of stack and $$$a_i$$$ are equal, then push $$$a_i$$$ to the stack, otherwise pop the top element and discard them both.

After this iteration, if the stack is empty then definitely no element occurs more than half of the times. Otherwise (note that at any moment of time all elements on the stack are equal) the top element is one possible candidate that can occur more than half of the times. Check that value.

Now as at any moment, the stack has equal elements, we can express the state of a stack by two numbers: $$$(x, \texttt{cnt}_x)$$$ — stack has $$$\texttt{cnt}_x$$$ elements of $$$x$$$.

We can merge two pairs, thus yielding a segment tree solution.

+14

This is really cool! Another solution is: if an element is super-frequent, it has to be the median. So you can calculate the median and check if it's super-frequent.

Is there any way of finding median in a range online in log2(n) without persistent segment trees?

I don't know any other way, but maybe someone does.

Yes, binary trie with sorted lists of occurrence indices (of leaves in the subtree) in each node. Then do fractional cascading on those lists.

martins

+15

Wavelet tree.

https://codeforces.net/blog/entry/52854

CSQ31

-10

you can log(n) with persistent segtree,instead of using the segtree in the binary search,you can simulate the binary search as you walk down the tree

ftiasch

+73

Another deterministic $$$O(q \log n)$$$ algorithm without tree-based data structures.

Suppose that the binary representation of $$$a_i$$$ is $$$b_{i, m - 1} \dots b_{i, 0}$$$ where $$$m = O(\log n)$$$.

The central observation is that if $$$a_i$$$ is the majority among $$$a_1, \dots, a_n$$$, $$$b_{i, j}$$$ is the majority among $$$b_{1, j}, \dots, b_{n, j}$$$. Therefore, we can find $$$b'_j$$$ which is the majority of $$$b_{1, j}, \dots, b_{n, j}$$$, and check whether $$$a' = b'_{m - 1} \dots b'_0$$$ is indeed the majority among $$$a_1, \dots, a_n$$$.

vishaaaal

Wow, that's elegant!

KeepMoving

hey anyone who solve problem B in problem B can we take same element more than one times??

spookywooky

It is not only that we can, it is that we must take same element more than one time.

This is because the rules say we need to maximize the sum of the elements while having the ANDsum==0.

This is only possible by setting each bit only once to zero, ie if n>k+1 there will by (by pigeon principle) the number with all bits set at least twice.

I have a doubt in problem B In problem B the sum of all elements in array is maximum but the value of maximum should be same or not for every size of array =n that we make for this conditions:- all its elements are integers between 0 and 2k−1 (inclusive); the bitwise AND of all its elements is 0; the sum of its elements is as large as possible

Sorry, I did not understand this.

one more doubt in editorial mention for each bit, we need to turn it off (make it 0) in at least one of the elements. Means we make that element equal to 0 ??

Try to solve the problem bit for bit. Each number has k bits, and those bits are independent of each other. To find an array fullfilling the rules we have to set each of those k bits in one number to 0, in all other numbers to 1.

Since it does not matter in which number we set the bit to 0, we have n^k different possibilities to do this.

and is the value of sum is same for all different possibilites??

Yes, it is allways the maximum possible sum.

daddy_puff

My approach for B: There will be n elements in the array. so to Maximize the sum, in (n-1) places we will place 2^k -1(maximum value) and at any one of the positions, we will place 0 so as to make the AND zero. But i am unable to understand where my approach will be wrong. Also just now i was thinking that instead of placing that zero couldn't we just put Complement of the maximum no. (2^k -1) ??? kindly help.

This aproach is correct. The maximum sum is (2^k-1) * (n-1). ie in one number all bits are set to zero.

However, the problem does not ask for that sum. It asks for the number of different arrays with that sum.

lautalom

hey there! I have a doubt in problem B, if someone would explain i'd be thankful.

If we have to "turn off" k bits in the array with $$$n$$$ elements of size $$$k$$$, what is wrong if you think have a fixed $$$n*k$$$ and then choosing any subset of $$$k$$$ elements, making the answer $$${{nk}\choose{k}}$$$ ?

dhruv7888

It is like choosing k elements from N*K elements , which can result in multiple no.s having the same bit off, which will give WA.

EJOI_Gold

https://codeforces.net/contest/1514/submission/113538267 Why this code shows Runtime error

Non-origination

I did C in a different way. We iterate through the numbers $$$1$$$ to $$$n-1$$$ and find the modular inverse for each of those numbers modulo n. In case the modular inverse of that number exists and is different from that number itself, we can include both the number and it's modular inverse in the product(as they pair up to give a product which is $$$1 \pmod n$$$).

Now for the case where a number is self invertible, i.e. of the form $$$x^2 \equiv 1 \pmod n$$$, we store those numbers separately. Except for the case where only one number is present in this list(namely the trivial solution $$$n-1$$$, which satisfies $$$(n-1)^2=1\pmod n$$$ always), it so happens(I think) that the product of the numbers in the list is $$$1 \pmod n$$$ always.

Formally, let $$$x_1,x_2,\ldots,x_k$$$ be the solutions to the equation $$$x^2 \equiv 1\pmod n$$$, with $$$k>1, 1<x_i<n \forall i$$$. Then $$$x_1x_2 \ldots x_k \stackrel{?}{\equiv} 1 \pmod n$$$. Can anyone prove this?

OptxPrime

Someone pasted this above, and it contains exactly what you are asking for: Link

rguy23

Please explain Problem E, I could not understand that Hamiltonian Path, this part? We find that it's from the grey node to the white node. We then put our grey node as the start of the path and continue doing that with the rest of the nodes, and we don't care which node will follow it, because the edge is out from the black node either way!

So the algorithm is as follows: you have $$$2$$$ paths, and you want to merge them into one. To do this, you'll ask about the direction of the edge between the first nodes in each of the paths, let's call them $$$u$$$ and $$$v$$$. If it's from $$$u$$$ to $$$v$$$, remove $$$u$$$ and append it to the merged path. Otherwise, do this to $$$v$$$. Why does this work? Suppose you append $$$u$$$. In the next step, either $$$v$$$ will be appended, which is great because there's an edge from $$$u$$$ to $$$v$$$, or the node after $$$u$$$ in the path will be appended, which is again great because then the edge clearly exists.

Ok, I understood this part, thanks but it is still confusing for me after this point also :(, using that 2n queries.

For each node, we want to get the edge that goes back as far as possible. Suppose we iterate over the path from the end to the beginning, and the current node is $$$u$$$. Currently, we know this node can go back to node $$$p$$$ by moving forward in the hamiltonian path then taking an edge that goes back to $$$p$$$. We want to see how the edges going back from $$$u$$$ itself affect $$$p$$$. To do this, we ask if there's an edge from $$$u$$$ to any of the nodes before $$$p$$$. While there is, we can safely keep decreasing $$$p$$$ because we know we can go back further. Once we're answered with $$$0$$$, we clearly can't decrease $$$p$$$ any further.

That takes $$$2n$$$ queries because if you receive $$$1$$$ as an answer, you decrease $$$p$$$, and if you receive $$$0$$$, you decrease $$$u$$$. Please see the code to support your understanding.

Yes, the sum for every array of size $$$n$$$ has to be the same and maximum which can be achieved by turning off exactly $$$k$$$ bits at distinct position as all the bits are initialized to $$$1$$$.

pratikraut0000

Can someone explain how is the probability of not choosing most frequent elements is 2^(-40) in Div2D randomisation solution ???

Since range of length l contains most frequent number more than l/2 times (if there is such element in range), probability of some element in range being equal to it is 1/2, and not being equal to it also about 1/2. So when we pick 40 numbers, probability that none of them is equal to super-frequent number is 1/2 * 1/2 * ... * 1/2 = (1/2)^40

ram2012k

For C Why the product is either 1 or n — 1 in the last ? can someone explain ?

Perry_Prasad_Platypus

+11

Muhammad98

weak pretests in A :(

Can someone explain me why p%n be a coprime as we are removing p , and also that in solution I got AC , why removing only the last coprime value worked for me ...

sh_maestro

1) To your first question:

I think the reason for this is that if you take two numbers (a, b) that are co-prime with the given number (n), then (a * b) % n will always be co-prime with n (and hence would be in our earlier list of all co-primes).

We can prove this by contradiction. Assume that weren't the case and you could have a remainder that's not co-prime with n (i.e. the remainder (r) has a factor that's greater than 1 common with n).

We know that both a and b are less than n, which means that g has to be a multiple of either a or b. In which case, one of a or b is not co-prime with n, contradicting our assumption that both a and b are co-prime with n.

2) To your second question, check out: https://math.stackexchange.com/questions/28913/consider-the-product-b-1-b-2-cdots-b-phim-when-is-this-congruent-to?noredirect=1&lq=1

Basically, the product of co-prime numbers (mod n) leading up to n is either 1 or -1. It's -1 in cases when there is a primitive root, otherwise its 1. Since, -1 is congruent to n — 1, in cases when you have a non-1 value remaining, (n — 1) needs to be divided as well.

Thanks for the explanations

generic_placeholder_name

Problem D is similar to several other codeforces problems. All of them give $$$O(n \log {n})$$$ solutions.

Also a ton of well-known $$$O(n \sqrt {n})$$$ solutions exist for the mode range query problem, but that's probably impossible to fail without failing the randomized solution as well.

munditva

I thought about solving the problems linked but returned after opening the links, reason being the problem tags showed 2500 and 3200.

I think most of the Div2 competitors might have never solved problems in that range.

Particularly I felt D was a nice problem although the idea may be old.

pikel_rik

Solution to bonus task for C: Here $$$\phi$$$ = euler's totient function. Some base cases: if $$$n$$$ is equal to 1, 2 or 4 the answer is 1. If $$$n$$$ is the power of an odd prime ($$$p^k, k \ge 1$$$) or twice the power of an odd prime ($$$2p^k, p > 2, k >= 1$$$), then the answer is $$$\phi(n) - 1$$$, else the answer is $$$\phi(n)$$$.

Apologies for the edits, there were more cases to consider than I realised.

yogi23

can you please explain the condition when "n is the power of an odd prime (pk,k≥1) or twice the power of an odd prime (2pk,p>2,k>=1), then the answer is ϕ(n)−1".Thanks!

+13

The answer depends on the number of solutions to $$$x^2 \equiv 1 \pmod n$$$. To actually compute the number of solutions, you can make us of this link.

Let $$$P$$$ is the product of all integers less than $$$n$$$ and coprime with it and that satisfy the above equation. Any integer that doesn't satisfy the above equation will multiply with its inverse to give 1 so we do not need to consider them.

Then we have two cases:

The number of solutions to the above equation is exactly 2. Then the solutions themselves will be exactly $$$1$$$ and $$$n - 1$$$. Then $$$P \equiv -1 \pmod n$$$ and we can just remove $$$n - 1$$$ to get a valid solution. This happens when $$$n$$$ is of the form $$$p^k$$$ or $$$2p^k$$$ where $$$p$$$ is an odd prime and $$$k \ge 1$$$.

Otherwise, $$$P \equiv 1 \pmod n$$$ and we can take all the numbers. I am not entirely sure how to prove this using only number theory though and I'd appreciate it if anyone provided such a proof.

I do know of a group theoretic proof of this fact though. The group theoretic results states that in any group $$$G, |G| > 2$$$ where all elements satisfy $$$x^2 = e$$$, the product of all its elements will be $$$e$$$ (the identity element, which in this case is $$$1$$$) and applying this result to $$$H = \{x \in (Z/nZ)^{\times} \mid x^2 = 1 \}$$$ gives us what we need.

gupta_samarth

There is a nice proof provided here.

Thank you!

ijxjdjd

Hamiltonian Path using insertion sort:

Consider a hamiltonian path $$$a_1 . . . a_k$$$ and a single node $$$x$$$ to add. If $$$a_k \rightarrow x$$$ or $$$x \rightarrow a_1$$$ obviously we can add to one of the ends. Otherwise, look for any index $$$i$$$ where $$$a_i \rightarrow x \rightarrow a_{i+1}$$$ to insert $$$x$$$ between. This can be done by binary search because the of the initial conditions $$$a_1 \rightarrow x$$$ and $$$x \rightarrow a_k$$$ (if $$$x \rightarrow a_{i}$$$ then there must be at least one index to the left where the condition is true, and vice versa for the opposite case). Total queries: $$$2n + \sum_1^n{\log{k}}$$$

PhantomAssassin

-14

why is the second test in D so big? I think it would be better to small tests first, then I large ones so that the participant can understand that at least he is going right.

lkahtttou

Goooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooogleforces

perec1970

Someone explain B with a concrete example.In detail. Thanks. Let's say there are n = 3 and k = 3 The array consists of the numbers 0 1 2 3 4 5 6 7 We need to find how many subarrays of length 3 with and equal to 0 and the maximum sum. Then how to see this formula that pow(n, k)?

fatemetmhr

You don't want to find a subarray, all you need is an array consist of n elements and each of them should be in range 0 — 7. So now you need to choose some bits to be 0.

Video Tutorial for Problem B (in detail) :)

https://www.youtube.com/watch?v=QnzTUWFx-B4

I_AM_RAHIMOV

another shit contest, realy!

WernerZiegler

In Problem D How does Randomly choosing 40 elements work?

limabeans

If an element is super-frequent on interval $$$[l,r]$$$, it has over $$$1/2$$$ chance to be chosen if we pick a random element. If we repeat this process $$$40$$$ times, the probability of hitting the super-frequent element at least once is $$$1-(1/2)^{40}$$$, so we're practically guaranteed to find the super-frequent element (if there is one) by just querying randomly enough times.

newbie_forever_at_cp

Actually I have a small doubt regarding rating change. In Div 1 round (round 712), https://codeforces.net/contest/1503/standings/participant/111887746#p111887746, I secured the rank 352 and I got rating update of 89 when I was 1973. Now in this round I secured 252 (div2 only rank 152), I got rating update of 63 from 1964. Could you pls tell me why is this difference ?

Proofy

In C, let the elements coprime to $$$n$$$ be $$$a_1, a_2, \dots , a_k$$$ where $$$a_1<a_2<\dots <a_k$$$. By Gauss's extension to Wilson's theorem we have that

$$$a_1\cdot a_2\cdots a_k \equiv -1 \equiv n - 1 \pmod{n} \, \, \text{if $$$n$$$ is $$$2$$$, $$$4$$$, $$$p_1^a$$$, $$$2p_1^a$$$}$$$

where $$$p_1$$$ is an odd prime and $$$a$$$ is a positive integer, and the product is equivalent to $$$1$$$ otherwise (by Gauss's extension). The above cases are the cases where in the editorial, $$$p \ne 1$$$, in this case we have that $$$p=n-1$$$ and the only element that we have to exclude is $$$n-1$$$ since it is also coprime with $$$n$$$. So, in fact, when the product modulo doesn't turn out to be $$$1$$$, it turns out to be $$$n-1$$$ and we exclude $$$n-1$$$ :)

DEAMN

Why in problem B answer is n^k? I don't understand editorial.

For the first bit in all the $$$n$$$ numbers (which all their bits are initially $$$1$$$) , you have to make exactly one bit to be equal to $$$0$$$ and you have $$$n$$$ choices for that , and the same for the second bit .. up to the $$$k−th$$$ bit , so it becomes $$$n∗n∗n...∗n$$$ k times, which is obviously $$$n ^ k$$$.

But u can make 2 bits to equal 0.Like n=3,k=3 => 5 6 3

I meant one single bit from (the first bit of all $$$n$$$ numbers)

racsosabe

You want the values to have Bitwise AND 0, so for each bit you need at least one element that has it off. Since you want to maximize the sum of elements, you must have only one such element and the rest will have that bit on.

Thus, for each bit you can choose any of the $$$n$$$ elements to have it off and there are $$$k$$$ independent bits. Thus, you can distribute the $$$0$$$s in $$$n^{k}$$$ ways.

shiftyblock

antixorz

+20

For D's randomized solution, we don't need upper bound check. We just need to check if occurence[lower_bound + ceil(x/2)] is in the range or not. Saves half the time I think.

RegoNoShi

Good catch but I think it should be occurrence[lower_bound + floor(x/2)]. But this helps only to check if an element is present more than x/2 times. You still need the upper bound to compute f, right?

Indeed but that puts time per operation to (iterations * logN) + logN as you only need to do upper bound once you've found such element per query.

Monogon

In E, you can do insertion sort as follows. Say the path of the previous nodes is $$$x_1, \ldots, x_k$$$ and we are inserting node $$$y$$$. If a directed edge $$$y\to x_1$$$ exists, we can insert $$$y$$$ in the beginning, or if a directed edge $$$x_n\to y$$$ exists, we add it to the end. Otherwise, we binary search to find an adjacent pair $$$x_i$$$ and $$$x_{i+1}$$$ such that $$$x_i\to y\to x_{i+1}$$$ and we can insert it there, giving us a new Hamiltonian path. This requires $$$2+\log n$$$ queries.

Interestingly, you don't even need those two queries for the beginning and end. It might not create a Hamiltonian path, but we can still finish the solution in $$$2n$$$ queries. Even though it might not be a Hamiltonian path, we can still guarantee that the nodes appear in an order so that the strongly connected components are disjoint segments, appearing in an order so that all edges between different components point to the right. In my solution, I don't care how the nodes are ordered within a component.

We will initialize all components as having only one element. Scan the nodes from left to right. For a node $$$x$$$, ask a query of type $$$2$$$ to see if it has a directed edge to any component to the left. If so, merge it with the previous component and repeat. Otherwise, move on to the next node. We can merge at most $$$n-1$$$ times and we can advance to the next node at most $$$n-1$$$ times, so we ask at most $$$2n$$$ queries of type $$$2$$$.

r57shell

I got accepted for 1514D - Cut and Stick using segment tree with occurrences of two most frequent values. And then, because count taken from segment tree is wrong, I found their count using lower_bound and upper_bound. Is it correct? Can someone proof it or hack it? 113549125

There's at most 1 super-frequent element in any interval, and your segment tree is guaranteed to find it if it exists. Otherwise, it doesn't really matter if your segment tree finds the wrong frequencies because the answer won't change (it's $$$1$$$).

Ok. It's a bit confusing, because this solution is (n + q) log n, and it's from editorial. What's a point in "bonus" then?

Something is missing. If I look for single frequent it doesn't work 113557958. This means that either my code is wrong, or this claim about "it will find super-frequent" is wrong.

My claim about super-frequent is based on the Deterministic solution in the editorial. Does your code do the same logic as the editorial, or something different?

In very first comment of this branch I described that I store number of occurrences of two frequent numbers in segment tree. If you looked carefully into editorial, you could notice difference: I store occurrences, they don't: they propose to get actual number of occurrences (for example with lower_bound/upper_bound). Second submission store single frequent number instead of two and get WA.

dark___horse

Can someone explain in question b what exactly did the third constraint on the array largest sum possible meant ?? I mean was this constraint on the array of any use ? Please explain with a proper testcase.

My approach was to select two numbers from n numbers for an array whose bitwise & is zero and take the remaining n-2 elements as the largest no. possible that is 2^k-1 . so we have 2^(k -1) possible ways to select those 1st two numbers and remaining n-2 nos. are same . now i calculated the permutations for each such array . in this approach i was getting less answer .

For Ex for n=3 k=3 i got 21 where as the answer was 27

pairs of first 2 nos. formed were (5,2) , (6,1) ,(3,4) , (7,0) and i paired them with 2^k-1 that is 7 so for 5 2 7 array 3! ways similarly for 6 1 7 , 3 4 7 3! each and finally for (7 0 7) 3 ways total 21 . please help..

how about (3 5 6)?

You can basically take one number to be 0 and all other numbers to be $$$ 2^k - 1 $$$, but then you notice that you can actually swap the 0 bit in the number 0 with any of the numbers.

Another way to think about it is, imagine writing the numbers in an n x k table, each column must contain a 0 ( to make bitwise AND 0 ), and to maximize sum you would want that each column contains exactly one 0.

Ingenious

in question C I came to a result which is like that:

Yes, if $$$ gcd(p,n) = 1 $$$, then there exists modular multiplicative inverse of $$$ p \mod n $$$, i.e. such number $$$ y $$$ that, $$$ y * p = 1 \mod n $$$. So then you multiply by $$$ y $$$ on both sides.

Using Bezout's identity you know that $$$x * p + y * n = 1$$$ has solutions which exactly means that p has multiplicative inverse, so you can multiply both sides by $$$p^{-1}$$$ and you get this result. Summary: you can divide by any co-prime with modulo.

tdas

Why stable_sort works in E? I thought that every std::sort method should follow Strict Weak Ordering or weird things may happen.

std::stable_sort uses less comparisons on average than std::sort. You can read some more from this blog and the comments.

mohamedeltair

In problem $$$D$$$, the claim Observe that if a range has a super-frequent element, and we split it into 2 ranges, then this element must be super-frequent in one of them. is not correct using the given definition for super-frequent. e.g., in the following array:

[1, 2, 1, 1, 2, 1]

1 is super-frequent in the whole range, but not super-frequent in both of the range halves, as it occurs exactly $$$\lceil \dfrac{length}{2} \rceil$$$ times in both of them.

I think the claim should be: If a range has an element occurring at least $$$\lfloor \dfrac{length}{2} \rfloor + 1$$$ times, and we split it into 2 ranges, then this element must occur at least $$$\lfloor \dfrac{length}{2} \rfloor + 1$$$ times in one of them.

saurabh2311

For C, editorial says "product won't be coprime with n, so when you take it modulo n, it can't be 1".Why cant it be 1?

When $$$v$$$ $$$mod$$$ $$$n$$$ $$$=$$$ $$$1$$$, it means that $$$v=k*n+1$$$. Hence, $$$v$$$ is coprime with $$$k*n$$$, because $$$x$$$ and $$$x+1$$$ are always coprime. Since $$$n$$$ is a divisor of $$$k*n$$$, $$$v$$$ is coprime with $$$n$$$ as well.

Pro_iq

can somebody explain why the answer is pow(n,k) i cant understand

If AND of some number is 0, then there should be at least one number which have the ith bit 0 (for each i from 0 to k — 1). Also you need to make the array in the way that sum of all elements is maximum possible so you need to have exactly that k bits zero and others should be one, now you just want to choose for each k bits which of the numbers have this 0 bit. Also one number may have several 0 bits, so the answer is pow(n, k).

can you explain the case when n<k

n = 3, k = 5

Now you need to choose 5 bits. For example:

01110

11001

10111

here I made 2 of them from the first element, 2 of them form second element, and the last one form the last number in the array. AND of this numbers is 0;

Another examples:

00000

11111

(all bits form the first element)

01010

10101

(3 bits from the first, 0 form the second, 2 form the last)

10001

01111

11110

so if you just determine which element will have the ith bit 0 then you can have a valid array. And for every k bit you have n choice, so the answer is pow(n, k)

Vratadharaya

Personally I don't like this way of editorial. Round 715 editorial was so good , at least try to give some hints before the actual idea , so that we can figure out our mistakes before arriving on the correct approach .

NGUYEN_THANH_LOI

Problem C. "If p is 1, you can take all these elements. Otherwise, you should take them all except for p" Why? I don't understand. Could you help me? Thank you so much.

tensor_shock

In the randomized solution of D how do we get 40 as the optimal number of tries? I am getting TLE for 60

swiftqwq

Because the number of the super-frequent element is more than $$$\frac{|len|}{2}$$$ , the pobability that you can find it when you try $$$x$$$ times is $$$\frac{1}{2^x}$$$, and $$$\frac{1}{2^{40}}$$$ is very small,so we use 40 (of course you can use some number smaller,like 30)

Can someone explain why this approach is wrong for problem B

maximum sum is (2^k — 1) * (n-1)

eg. 4 3 have maximum sum 21 which i can get by (0, 7, 7, 7), (1, 6, 7, 7), (2, 5, 7, 7), (3, 4, 7, 7)

so i tried (2^(k-1) — 1) * (n choose 2) * 2 + n = ((2^(k-1) — 1) * n * (n-1)) + n

multiply 2 for substituting the two numbers (eg. (1, 6), (6, 1)) and adding n for case of 0 is n choose 1

Why is this solution wrong?

termi9929

same bro

Well i understood it after reading the tutorial many times

there are some other cases like (3, 5, 6, 7) have summation 21 and And bitwise is 0

I hope you can understand it in this way:

For a single bit i, it has n ways to be 0 (n choose 1)

let Xi = number of ways for bit i

So the total number of ways is X0 * X1 * .... * X(k-1) which is n * n * ... * n = n^k

same here bro

I explained it above

jac_nikola

I couldn't solve C during contest. But I came across this interesting observation:

Let $$$[x_0,x_1,...,x_p]$$$ $$$(x_i < n)$$$ be the longest subsequence whose product is $$$1$$$ modulo $$$n$$$. We can also write those numbers as $$$[(n-y_0),(n-y_1),...,(n-y_p)]$$$. The product of these numbers = $$$J \pm y_0.y_1....y_p$$$, where $$$J$$$ is the sum of terms involving powers of $$$n$$$, so obviously $$$J$$$ $$$mod$$$ $$$n$$$ $$$= 0$$$. Therefore $$$y_0,y_1....y_p$$$ has to be the longest subsequence whose product is $$$1$$$ modulo $$$n$$$, i.e $$$[y_0,y_1....y_p] = [x_p,x_{p-1}....x_0]$$$. In short this means if $$$x_i$$$ appears in my required longest subsequence then $$$(n-x_i)$$$ also must appear in the subsequence (not always true for $$$x_i = 1$$$). So we can say the required subsequence is spread symmetrically about $$$n/2$$$ in the number line.

Retarded_Ape

For the bonus task of C, where n<=10^12, what if n is a prime number, because if n is a prime number, we will have to print atleast n-1 integers. How are we going to do that?

I guess Time limit for that would be 3 hour then

d_sqaure

20 months ago, # ^ |

I also had same doubt.Thanks, you clarified!. Btw we can count according to above comment by pikel_rik

I don't even know what I am talking about in this comment about 22 months ago lol. Thanks for the reply though. Logged in after a long time, felt good!

Sorry bhai galti se downvote ho gya.

Google.cpp

what is the trick for problem D to reduce time complexity to O(nrootn) from O(nrootnlogn)

like if i store array instead of map then it will give me memory limit exceeded

sleepwalking643

Problem D, how our randomized 40 numbers, each have the probability of 1 / 2 being a super frequent element? Can someone explain please ^^;

WolfBlue

We check a interval to see if it contains a super frequent element by choosing elements randomly. If it does not have a super frequent element, then each check will surely fail, as we desire. On the other hand, if it does have a super frequent element, then by definition, that element appears in more than half of the positions in the interval, so choosing if the element at a random position in the interval is a super frequent element will succeed with probability more than one half.

chty_syq

Problem E.

Why the merge sort in editorial could be implemented by sort()?

kpw29

Well, merge sort is one of the sorting algorithms. Stable_sort guarantees stability, which is achieved by mergesort. So that's why the author calls just that function with a custom comparator (OneEdge) to find the Hamiltonian path.

Thank you, I worried if there is a ring when sorting. I have solved it. The vertex in graph is like a partiallyordered set. We just have to get one correct path.

WenDavid552

Maybe we can use a persistent segment tree to obtain an algorithm of O(nlogn) for problem D.

tj-black

I found this nice video that clearly explains the following statement for Problem C. Product 1 Modulo N.

For two numbers $$$a$$$ and $$$b$$$ that are co-prime with $$$n$$$, if $$$q$$$ $$$=(a*b)$$$ % $$$n$$$ then $$$q$$$ is co-prime with n.

Oryon

Thank you for sharing!

xodeChemist

thank you for this video link

happypeople

I hava a problem about 1514D-Cut and Stick.

I use srand(0) function to initialize, use the rand function,and loop 40 times.

But i can't accept it. It's Wrong answer. When looping 80 times, it will Timelimit out.

When i use rand * rand, i can accept it.

Why?

rosklin

I think it is because you didn't multiply by 1ll when use only one rand().

I tried multiplying 1ll, but it is still a wrong answer. The return value of the rand function is integer.

ljuba

I guess that you are getting WA because you don't use Mersenne Twister.

Check out this blog: Don't use rand(): a guide to random number generators in C++

thank you

hope...

I'm agree with you, but I'm just curious why we can't use this (rand() << 15) | rand() to get randomized number that bigger than 32767, and use XOR rand()^rand() to get more randomized number ?

So finally it's look like ((rand() << 15) | rand()) ^ ((rand() << 15) | rand()).

Got the answer here https://codeforces.net/blog/entry/61587?#comment-784640

SarthakBansal

Can someone please explain to me what do you even mean by 1 modulo n, in Problem C?

In sample case they say 1 modulo 5 is congruent to 6, but I just googled it and it said 1.

We say $$$v_1$$$ and $$$v_2$$$ are congruent $$$mod$$$ $$$n$$$ if both can be written as $$$c_1*n+1$$$ and $$$c_2*n+1$$$ for some arbitrary constant integers $$$c_1$$$ and $$$c_2$$$. This holds for $$$1$$$ and $$$5$$$ $$$mod$$$ $$$6$$$, $$$i.e.$$$, $$$1=0*5+1$$$ and $$$6=1*5+1$$$.

-_o

In problem C, I didn't get the point why does it obvious that we only need to exclude the element which equals to product modulo n to get the subsequence, product of which modulo n would be exactly 1. Could someone explain it?

Let p = product of the numbers of the required longest subsequence. We're not worried right now if it's made up of coprimes or not.

We can write, p = n*m + r ---- (1)

Now let's say for some d > 1:

d divides p and also d divides n => d divides r (From (1)) => r != 1

That means no d > 1 should divide both p and n => p and n should be coprime with each other => p should be the product of coprimes of n.

Now let's prove that r should also be a coprime of n.

Let's assume r is not a coprime of n. Then we can write r = a*b and n = a*c, for some a > 1.

Therefore (1) can be written as p = a*(b*m + c) => p can be written as p = a*e.

But this is a contradiction since p and n are coprimes to each other, so they both shouldn't contain any same divisor.

Therefore r must also be a coprime of n. Also, r < n as r is the remainder.

Therefore r must be a coprime that is already present in the subsequence. If r != 1, we simply divide p by r.

Note: From (1) since r is divisible by r and p is divisible by r so n*m must also be divisible by r.

Many thanks! I finally got it. The last paragraph answers my question.

t17

https://codeforces.net/contest/1514/submission/113533888

Why I am getting runtime error on problem D.

Update: why so many downvotes.

update: Ok ,I got it. I'm sorry for my mistake. now above link is working.

28CM31E122228E2H8H230ML

okay i do not get this one,

int query(int node,int st,int en,int l,int r)
{
    if (en<l || st>r || r<l)
    return 0;
    if (l<=st && en<=r)
    return cnt(l,r,tree[node]);
    int mid=(st+en)/2;
    return max(query(2*node,st,mid,l,r),query(2*node+1,mid+1,en,l,r));
}

In left and right nodes say there is same element that occurs with max frequency in both of them, why do not you return the sum of them ? As currently you are returning the max of them. mohammedehab2002

Notice this line:

if (l<=st && en<=r)
return cnt(l,r,tree[node]);

This is the base case. When I find a range fully inside my query interval, I don't return this element's count in that range; I return this element's count in the whole query interval, so taking the max is the right way to go.

Oooops , missed that !! thanks for clarifying. :)

ALT__

I'm unable to understand B :( Can someone explain with an example? thx

Found it, if someone else is looking for a good explanation, here: https://codeforces.net/blog/entry/89810?#comment-782301

For problem E,can someone tell me how can you make a connection between hamiltonian path and the problem,I think it's not very usual.

Jobaidul

D number is similar to this (SPOJ — PATULJCI) problem

Aman_j1

3 years ago, # |

Problem D is very similar to this problem: https://leetcode.com/problems/online-majority-element-in-subarray/

hydra_cody

16 months ago, # |

← Rev. 5 →

Can anyone explain the merge process of Cut and Stick on solving with the third approach?


std::pair<int, int> merge(std::pair<int, int> a, std::pair<int, int> b) {
    std::pair<int, int> res;
    if(a.first == b.first) {
      res = {a.first, a.second+b.second};
    }
    else if(a.second > b.second) {
      res = {a.first, a.second-b.second};
    }
    else {
      res = {b.first, b.second-a.second};
    }
    return res;
}

Why do we subtract the two?